- •Бельфер Рувим Абрамович
- •Технический редактор е. Зорин
- •Глава 3. Физический уровень сети пакетной коммутации 46
- •Глава 4. Информационные процессы на канальном уровне сети х.25 59
- •Глава 5. Структурные схемы программного обеспечения процедуры управления потоками сети X.25 73
- •Глава 6. Информационные процессы на сетевом уровне сети X.25 121
- •Глава 7. Структурные схемы программного обеспечения функций сетевого уровня сети X.25 130
- •Глава 8. Сеть Frame Relay 152
- •Глава 9. Сеть atm. Физический уровень 166
- •Глава 10. Сеть atm. Канальный уровень 178
- •Глава 11. Первичные сети уплотненного волнового мультиплексирования 192
- •Глава 12. Ip-сети. Стек протоколов tcp/ip и их функции 196
- •Глава 13. Ip-сети. Межсетевой уровень. Протоколы безопасности 204
- •Глава 15. Сети mpls 237
- •Глава 16. Виртуальные частные сети 253
- •Глава 18. Ip-телефония 297
- •Глава 19. Управление сетью сигнализации окс№7 321
- •Глава 20. Интеллектуальные сети 332
- •Глава 21. Сети стандарта gsm 346
- •Глава 22. Система окс№7 в gsm. Информационная безопасность окс№7 в ссоп 367
- •Глава 23. Сети сотовой связи стандартов gprs, edge и umts 384
- •Глава 24. Беспроводные локальные сети стандартов 802.11 416
- •Глава 25. Сети WiMax и lte 433
- •Глава 8. Сеть Frame Relay
- •Глава 9. Сеть atm. Физический уровень
- •Глава 10. Сеть atm. Канальный уровень
- •Глава 11. Первичные сети уплотненного волнового мультиплексирования
- •Глава 12. Ip-сети. Стек протоколов tcp/ip и их функции
- •Глава 13. Ip-сети. Межсетевой уровень. Протоколы безопасности
- •Глава 18. Ip-телефония
- •Глава 19. Управление сетью сигнализации окс№7
- •Глава 20. Интеллектуальные сети
- •Глава 21. Сети стандарта gsm
- •Глава 22. Система окс№7 в gsm. Информационная безопасность окс№7 в ссоп России
- •22.2.1. Вызов мобильной станции из ТфОп/isdn и обеспечение защиты приватных данных местоположения абонента-роумера
- •Глава 23. Сети сотовой связи стандартов gprs, edge и umts
- •Глава 24. Беспроводные локальные сети стандартов 802.11
- •Глава 25. Сети WiMax и lte
- •Глава 26. Самоорганизующиеся сети son
- •Глава 1. Единая сеть электросвязи России и актуальность информационной безопасности сетей связи
- •1.1. Роль и место есэ
- •1.2. Классификация сетей связи
- •1.3. Иерархический принцип построения ТфОп и gsm России
- •1.4. Актуальность информационной безопасности сетей связи
- •Глава 2. Стек протоколов сети пакетной коммутации X.25. Шифрование информации в сети
- •2.1. Многоуровневый принцип построения сети
- •2.2. Службы с установлением и без установления соединений, надежные и ненадежные соединения
- •2.3. Пакетная коммутация
- •2.4. Стек протокола сети пакетной коммутации стандарта X.25
- •2.5. Шифрование сообщений в сети пакетной коммутации
- •Глава 3. Физический уровень сети пакетной коммутации
- •3.1. Архитектура физического уровня
- •3.2. Физическая среда передачи информации
- •3.3. Аналоговая и цифровая связь
- •3.4. Модем и цифровая абонентская линия adsl
- •3.5. Аналого-цифровое преобразование
- •3.6. Цифровое кодирование и синхронизация
- •3.7. Частотное и временное мультиплексирование
- •3.7.1. Частотное мультиплексирование
- •3.7.2. Методы построения аппаратуры частотного мультиплексирования
- •3.7.3. Временное мультиплексирование
- •Глава 4. Информационные процессы на канальном уровне сети х.25
- •4.1. Временная диаграмма последовательности обмена кадрами
- •4.2. Формат кадра
- •4.3. Восстановление информационных кадров
- •4.4. Обнаружение ошибок с помощью избыточного циклического кода
- •4.4.1. Пример с использованием арифметики по модулю 2
- •4.4.2. Пример с использованием полинома
- •4.4.3. Пример аппаратной реализации
- •Глава 5. Структурные схемы программного обеспечения процедуры управления потоками сети X.25
- •5.1. Структурная схема организации по процедуры управления потоками сети х.25
- •5.2. Структурные схемы фоновых программ
- •5.2.1. Основные положения составления по. Структурная схема р1пд «Запрос и прием очередного пакета с 3 уровня»
- •5.2.2. Структурная схема программы р2пд - «Подготовка к передаче очередного «I» кадра в канал»
- •5.2.3. Структурные схемы программы р1пм - «Обработка принятых кадров «I»» и программы р2пм – «Обработка принятого кадра rr»
- •5.2.4. Структурная схема программы p2пм - «Обработка принятого кадра rr»
- •5.2.5. Структурные схемы программ p4пд - «Передача кадра rr» и р5пд – «Передача кадра rej»
- •5.2.6. Структурная схема программы р3пм - «Обработка принятого кадра отрицательной квитанции rej»
- •5.2.7. Структурная схема программы р3пд - «Подготовка к передаче «I» кадра по rej»
- •5.2.8. Структурная схема программы р6пд - «Анализ перехода в режим повторения передачи кадра по таймеру»
- •5.2.9. Структурная схема программы р7пд - «Подготовка к передаче «I» кадра по таймеру»
- •5.2.10. Структурная схема программы р4пм - «Установление и снятие запрета на передачу «I» кадров»
- •Программа p1
- •1.2. Программа p2
- •1.3. Программа p3
- •1.4. Программа p4
- •1.5. Программа p5
- •2.1. Программа p6
- •2.2. Программа p7
- •2.3. Программа p8
- •2.4. Программа p9
- •2.5. Программа p10
- •2.6. Программа p11
- •2.7. Некоторые характеристики контрольного примера
- •3.1. Программа p1
- •3.2. Программа p2
- •3.3. Программа p3
- •3.4. Программа p4
- •3.5. Программа p5
- •3.6. Исходные данные для лабораторной работы
- •4.1. Программа p6
- •4.2. Программа p7
- •4.3. Программа p8
- •4.4. Программа p9
- •4.5. Исходные данные для лабораторной работы
- •5.1. Программа p10
- •5.2. Программа p11
- •5.3. Программа p12
- •6.1. Программа p6
- •6.2. Программа p7
- •6.3. Программа p8
- •6.4. Программа p9
- •6.5. Программа p10
- •6.6. Исходные данные для лабораторной работы
- •Глава 6. Информационные процессы на сетевом уровне сети X.25
- •6.1. Принцип установления виртуальных каналов в сети х.25
- •6.2. Диаграмма установления коммутируемого виртуального канала
- •6.3. Особенности протокола сетевого уровня х.25
- •6.4. Услуга информационной безопасности «Замкнутая группа абонентов»
- •Глава 7. Структурные схемы программного обеспечения функций сетевого уровня сети X.25
- •7.1. Структурная схема организации по функций сетевого уровня сети х.25
- •7.1.1. Структурная схема программы Ррасп «Распределение принятых пакетов из канальных процессоров в очереди по типам»
- •7.2. Структурные схемы программ формирования таблицы маршрутизации по логическим канальным номерам lcn
- •7.2.1. Структурная схема программы “Обработка пакетов "Запрос Вызова"”
- •7.2.2. Структурная схема программы “Обработка пакетов "Вызов Принят"”
- •7.3. Структурная схема программы "Коммутация пакетов "данные""
- •7.1. Программа p1
- •7.2. Программа p2
- •7.3. Программа p3
- •7.4. Программа p4
- •7.5. Программа p5
- •7.6. Программа p6
- •7.7. Программа p7
- •Исходные данные для лабораторной работы
- •Алгоритм программы "Коммутация пакетов "данные"
- •Программа lab8 выполняет функции структурной схемы программы Коммутация пакетов "данные" (см. Глава 7).
- •8.1. Программа p1
- •8.2. Программа p2
- •8.3. Программа p3
- •Глава 8. Сеть Frame Relay
- •8.1. Стек протоколов сети Frame Relay
- •8.2. Поддержка качества обслуживания
- •8.3. Типы виртуальных каналов в сети fr
- •8.4. Установление коммутируемого виртуального канала
- •8.5. Виртуальная частная сеть на основе сети Frame Relay
- •8.6. Стандарт itu-t g.1000 (sla)
- •8.7. Соглашение об уровне обслуживания сети Frame Relay
- •8.8. Особенности сети Frame Relay по сравнению с сетью х.25
- •Глава 9. Сеть atm. Физический уровень
- •9.1. Основные положения и стек уровней сети атм
- •9.2. Физический уровень atm
- •9.2.1. Подуровень физического уровня атм «Конвергенция передачи»
- •9.2.2. Подуровень физической передающей среды atm на базе рdн
- •9.2.2.1. Недостатки pdh
- •9.2.3. Подуровень физической передающей среды atm на базе sdh
- •9.2.3.1. Иерархия скоростей
- •9.2.3.2. Типы оборудования sdh
- •9.2.3.3. Стек протоколов sdh
- •9.2.3.4. Структура кадра stm
- •9.2.3.5. Топологии связей в sdh
- •Глава 10. Сеть atm. Канальный уровень
- •10.1. Уровень atм
- •10.1.1. Поле идентификаторов виртуального пути и виртуального канала
- •10.2. Параметры трафика и показатели качества обслуживания
- •10.3. Уровень адаптации атм
- •10.4. Сигнализация и маршрутизация в сети atm
- •10.4.1. Стек протоколов при установлении коммутируемого виртуального канала
- •10.4.2. Протокол pnni по выполнению функции маршрутизации
- •10.4.3. Протокол по выполнению функции сигнализации pnni
- •10.5. Управление atm-трафиком в процессе передачи
- •10.5.1. Контроль трафика
- •10.5.2. Контроль перегрузки
- •10.6. Виртуальная частная сеть на основе сети atm
- •10.7. Особенности сети атм по сравнению с сетью Frame Relay
- •Глава 11. Первичные сети уплотненного волнового мультиплексирования
- •11.1. Основные функции dwdm
- •11.2. Принцип работы dwdm
- •11.3. Типовые топологии
- •Глава 12. Ip-сети. Стек протоколов tcp/ip и их функции
- •12.1. Стек протоколов тср/ip
- •12.1.2. Транспортный уровень стека tcp/ip
- •12.1.3. Межсетевой уровень стека tcp/ip
- •12.2. Пример переноса данных в ip-сети
- •12.3. Протоколы tcp/ip
- •12.3.1. Протокол прикладного уровня snmp
- •12.3.2. Протокол транспортного уровня tcp
- •Глава 13. Ip-сети. Межсетевой уровень. Протоколы безопасности
- •13.1. Протоколы межсетевого уровня
- •13.1.1. Формат ip-пакета
- •13.1.2. Принцип маршрутизации
- •13.1.3. Внутренние и внешний протоколы маршрутизации
- •13.1.3.1. Протокол rip
- •13.1.3.2. Протокол ospf
- •13.1.3.3. Протокол bgp
- •13.2. Протоколы информационной безопасности
- •13.2.1. Протокол прикладного уровня pgp
- •13.2.2. Протокол сетевого уровня ipSeс
- •13.2.2.1. Заголовки ipSec
- •13.2.2.2. Транспортный и туннельный режимы
- •13.2.2.3. Защищенные связи
- •13.2.2.4. Виртуальная частная сеть vpn-ipSec
- •13.2.3. Протокол транспортного уровня tls
- •13.2.3.1. Передача данных при использовании tls
- •13.2.3.2. Установление защищенной связи
- •13.2.4. Протоколы иб при маршрутизации
- •Глава 14. Интегральное и дифференцированное качество обслуживания. Стандарты QoS в ip-сетях
- •14.1. Качество обслуживания
- •14.2. Интегральное обслуживание IntServ
- •14.3. Дифференцированное обслуживание DiffServ
- •14.3.1. Модель DiffServ
- •14.3.2. Структурная схема программного обеспечения обработки очередей в модели DiffServ
- •14.4. Стандарты по качеству обслуживания в ip-сетях
- •14.4.1. Рекомендация itu-t y.1540
- •14.4.2 Рекомендация itu-t y.1541
- •Глава 15. Сети mpls
- •15.1. Принцип работы сети mpls
- •15.1.1. Маршрутизатор коммутации меток (lsr)
- •15.1.2. Граничный маршрутизатор коммутации меток (ler)
- •15.2. Стек меток
- •15.3. Маршрутизация пакетов в узле коммутации lsr
- •15.4 Распределение меток
- •15.4.1 Протокол распределения меток ldp
- •15.5 Инжиниринг трафика
- •15.5.1. Пример выбора путей
- •15.6. Быстрая ремаршрутизация
- •15.7. Преимущества mpls по сравнению с ip-сетью
- •Глава 16. Виртуальные частные сети
- •16.1. Туннелирование mpls
- •16.2. Виртуальная частная сеть mpls третьего уровня (mpls l3vpn)
- •16.2.1. Общая модель mpls l3vpn
- •16.2.2. Таблицы маршрутизации в vpn
- •16.2.3. Формирование таблицы маршрутизации сообщениями mp-bgp
- •16.2.4. Пересылка пакетов в vpn
- •16.2.5. Формирование топологии vpn
- •16.2.6. Сравнение vpn-технологий
- •Обеспечение качества обслуживания
- •Масштабируемость
- •Информационная безопасность
- •Гибкость создания сети
- •Гибкая адресация
- •Объединение различных типов данных
- •Инжиниринг трафика
- •Сложность проектирования
- •Глава 17. Цифровая сеть с интеграцией служб. Общеканальная сигнализация окс№7
- •17.1. Цифровая сеть с интеграцией служб isdn
- •17.1.1. Структура сети isdn
- •17.1.2. Абонентский доступ сети isdn
- •17.1.2.1. Функции физического и канального уровней
- •17.1.2.2. Функции сетевого уровня
- •17.2. Общеканальная сигнализация окс№7
- •17.2.1. Принцип работы окс№7 в сети ТфОп/isdn
- •17.2.2. Стек протоколов окс№7 в сети ТфОп/isdn
- •17.2.3. Диаграмма установления соединения в системе окс№7 isdn
- •17.2.4. Протокол подсистемы передачи сообщений mtp
- •17.2.4.1. Уровни подсистемы передачи сообщений mtp
- •17.2.4.2. Функции звена данных сигнализации (уровень 1, мтр1)
- •17.2.4.3. Функции звена сигнализации (уровень 2, мтр2)
- •17.2.4.4. Функции сети сигнализации (уровень 3, мтр3)
- •17.2.4.5. Функции обработки сигнальных сообщений
- •17.2.4.5.1. Маршрутизация сигнальных сообщений
- •17.2.4.6. Требования к показателям качества обслуживания мтр
- •17.3. Подсистема пользователя isup
- •17.4. Аутентификация пользователя в сети isdn
- •17.4.1. Аутентификация пользователя с помощью pin-кода
- •17.4.2. Аутентификация пользователя с помощью tan
- •17.5. Аутентификация объектов аудиовизуальной службы сети isdn и создание общих секретных ключей взаимодействующих объектов
- •Сравнивая приведенный алгоритм с протоколами ipSec и tls (глава 13), можно заметить тот же самый принцип, что и при установлении защищенной связи. Глава 18. Ip-телефония
- •18.1. Протокол sip
- •18.1.1.Упрощенный пример сети на базе протокола sip
- •18.1.2. Cетевые компоненты протокола sip
- •18.1.3. Сообщения sip
- •18.1.3.1. Поля заголовка сообщения при регистрации sip
- •18.1.3.2. Транзакции и диалоги sip
- •18.1.3.3. Маршрутизация сообщений sip
- •18.1.4. Протокол sip-t
- •18.2. Информационная безопасность sip
- •18.2.1. Угрозы иб
- •18.2.1.2. Подмена сервера
- •18.2.1.4. Прерывание сеанса связи
- •18.2.1.5. Отказ в обслуживании
- •18.2.2. Требования к способам обеспечения иб в сети sip
- •18.2.3. Механизмы обеспечения иб
- •18.2.3.1. Механизм иб sip-сети на базе протокола ipSec
- •18.2.3.2. Механизм иб sip-сети на базе протокола tls
- •18.2.3.3. Механизм иб sip-сети на базе протокола s/mime
- •18.2.3.4. Механизм аутентификации пользователя в sip-сети на базе протокола http Digest
- •18.2.3.5. Аутентификация идентификатора пользователя
- •18.3. Транспортировка данных в сети sip
- •18.3.1. Протоколы транспортировки данных
- •18.3.2. Обеспечение иб при транспортировке данных
- •Глава 19. Управление сетью сигнализации окс№7
- •19.1. Управление сетью сигнализации
- •19.1.1. Управление сигнальным трафиком
- •19.1.1.1. Процедуры перевода трафика на резервное зс и возврата на исходное зс
- •19.1.1.2. Процедура вынужденной ремаршрутизации и управляемой ремаршрутизации
- •19.1.1.3. Процедура перезапуска мтр
- •19.1.1.4. Процедура управляемого переноса
- •19.1.1.5. Недоступность подсистемы isup
- •19.1.2. Управление звеньями сигнализации
- •19.1.3. Управление сигнальными маршрутами
- •19.2. Тестирование звена сигнализации
- •19.3. Пример отказа и восстановления сигнального звена сигнализации между исходящим и транзитным пунктами сигнализации
- •19.3.1. Алгоритм при отказе звена сигнализации
- •19.3.2. Восстановление звена сигнализации
- •19.4. Пример отказа и восстановления транзитного пункта сигнализации
- •19.4.1. Отказ транзитного пункта сигнализации
- •19.4.2. Восстановление транзитного пункта
- •Глава 20. Интеллектуальные сети
- •20.1. Принцип обслуживания вызовов в сети ТфОп/isdn на основе интеллектуальной сети
- •20.2. Подсистема sccp в стеке протоколов окс№7 интеллектуальной сети
- •20.2.1. Службы передачи сообщений
- •20.2.2. Управление маршрутизацией
- •20.2.3. Управление подсистемой sccp
- •20.2.4. Расширение адресации
- •20.3. Взаимодействие уровней окс №7 в сети in. Пример алгоритма представления услуги
- •20.4. Алгоритм аутентификации в протоколе услуги «универсальная персональная связь» интеллектуальной сети
- •20.5. Количественная оценка угроз безопасности интеллектуальной сети
- •Глава 21. Сети стандарта gsm
- •21.1. Классификация беспроводных сетей связи
- •21.2. Система gsm
- •21.2.1. Функциональная архитектура gsm
- •21.2.1.1. Подсистема радиосвязи
- •21.2.1.2. Подсистема сетей и коммутации
- •21.2.1.3. Операционная подсистема
- •21.2.2. Логические каналы и установление связи
- •21.3. Обработка речевых сигналов на радиоучастке
- •21.3.1. Кодер речи
- •21.3.2. Кодер канала
- •21.3.3. Модуляция
- •21.4. Информационная безопасность gsm
- •21.4.1. Конфиденциальность
- •21.4.2. Аутентификация пользователя
- •21.4.3. Защита приватных данных
- •Глава 22. Система окс№7 в gsm. Информационная безопасность окс№7 в ссоп
- •22.1. Архитектура протоколов передачи сигналов в gsm
- •22.2. Пример обработки вызова мобильной станции из ТфОп/isdn и управление мобильностью
- •22.2.1. Вызов мобильной станции из ТфОп/isdn и обеспечение защиты приватных данных местоположения абонента-роумера
- •22.2.2. Управление мобильностью
- •22.3. Принцип иерархии федеральной сети общего пользования gsm
- •22.4. Принцип построения системы окс№7 России
- •22.5. Информационная безопасность окс№7
- •22.5.1. Архитектура сетевой безопасности окс№7
- •22.5.1.1. Уровни безопасности окс№7
- •22.5.1.2. Плоскости безопасности окс№7
- •22.5.2. Атаки «отказ в обслуживании» DoS в окс№7
- •22.5.2.1. Примеры последствий воздействия атак DoS нарушения маршрутизации окс№7
- •Результаты анализа архитектуры сетевой безопасности окс№7 при воздействии атаки DoS процедуры маршрутизации
- •Глава 23. Сети сотовой связи стандартов gprs, edge и umts
- •23.1.1.1. Информационная безопасность gprs
- •23.1.2. Сети сотовой связи стандарта edge и показатели скорости передачи
- •23.1.2.1. Метод перескока частоты
- •23.2. Сети сотовой связи стандарта umts
- •23.2.1. Принцип работы cистемы cdma
- •23.2.2. Сравнение систем tdma/fdma и cdma
- •23.2.3. Сети сотовой связи стандарта umts
- •23.3. Информационная безопасность umts
- •23.3.1. Ограничения в обеспечении иб gsm
- •23.3.2. Классификация угроз иб в umts
- •23.3.3. Обеспечение защиты приватности местоположения мобильной станции
- •23.3.4. Взаимная аутентификация пользователи и сети
- •23.3.5. Установление алгоритмов обеспечения целостности сообщений и шифрования сообщений
- •23.3.6. Шифрование сообщений
- •Глава 24. Беспроводные локальные сети стандартов 802.11
- •24.1. Архитектура сети стандарта 802.11
- •24.2. Подуровень mac стандартов сетей Wi-Fi
- •24.3. Физический уровень стандартов сетей Wi-Fi
- •24.3.1. Базовый стандарт 802.11
- •24.3.2. Стандарт 802.11b
- •24.3.3. Стандарт 802.11a
- •24.3.4. Стандарт 802.11g
- •24.3.5. Стандарт 802.11n
- •24.4. Mesh-сети стандарта 802.11s
- •24.5. Стандарты информационной безопасности сети Wi-Fi
- •23.5.1. Протокол безопасности wep
- •24.5.2. Протокол безопасности wpa
- •24.5.2.1. Аутентификация
- •24.5.2.2. Конфиденциальность и целостность данных
- •24.5.3. Протокол безопасности 802.11i
- •Глава 25. Сети WiMax и lte
- •25.1. Общие положения
- •25.2. Физический уровень WiМах
- •25.2.1. Режим ofdm
- •25.2.2. Режим ofdmа и sofdmа
- •25.2.3. Канальное кодирование
- •25.3.1. Классы качества обслуживания
- •25.3.2. Подуровень безопасности
- •Глава 26. Самоорганизующиеся сети son
- •26.1. Функции самоорганизующихся сетей и область их использования
- •26.1.1. Сенсорные сети (wsn)
- •26.1.2. Ячеистые сети (wmn)
- •26.1.3. Автомобильные беспроводные сети (vanet)
- •26.2. Угрозы безопасности самоорганизующихся сетей
- •26.2.1. Перехват
- •26.2.2. Анализ трафика
- •26.2.3. Физические атаки
- •26.2.4. Фальсификация, повтор и изменение сообщений
- •26.2.5. Атаки DoS (“ отказ в обслуживании”)
- •26.2.5.1. DoS на физическом уровне
- •26.2.5.2. DoS на канальном уровне
- •26.2.5.3. DoS маршрутизации
- •26.3. Протоколы маршрутизации
- •26.3.1. Протоколы маршрутизации сети manet
- •26.3.1.1. Требования к протоколам маршрутизации в manet
- •26.3.1.2. Протоколы маршрутизации aodv и saodv
- •26.3.2. Протоколы маршрутизации беспроводной сенсорной сети
- •26.3.3. Протоколы защиты маршрутизации mesh-сети
- •26.3.4. Безопасность автомобильной беспроводной сети (vanet)
- •А.1. Задачи безопасности сетей связи
- •А.2. Архитектура безопасности сетей связи
- •А.2.1. Способы обеспечения информационной безопасности
- •Управление доступом
- •Аутентификация
- •Неотказуемость
- •А.2.3. Плоскости безопасности
- •А.2.4. Угрозы безопасности и способы обеспечения безопасности
- •А.2.5. Способы обеспечения иб в модулях безопасности
- •А.3. Метод количественной оценки угрозы безопасности сети связи
- •Приложение б. Шифрование с общим ключом
- •Б.1. Классификация методов шифрования
- •Б.2. Блочные шифры
- •Б.2.1. Методы перестановки и подстановки. Схема блочного шифрования
- •Б.2.2. Режимы блочного шифрования
- •Б.2.2.1. Режим электронного шифроблокнота (ecb)
- •Б.2.2.2. Режим группового шифра (ofb)
- •Б.3. Поточные шифры
- •В.2. Алгоритм rsa
- •В.3. Электронная цифровая подпись (эцп)
- •В.3.1. Требования к эцп
- •В.3.2. Эцп на основе шифрования профиля сообщения
- •В.3.2.1. Функция хеширования стандарта sha-1
- •В.3.2.2. Применение sha-1 и rsa для создания эцп
- •В.3.3. Управление открытыми ключами
- •В.3.3.1. Угроза «человек посередине»
- •В.3.3.2. Сертификаты
- •В.3.3.3. Стандарт сертификатов х.509
- •Одношаговая аутентификация
- •Двухшаговая аутентификация
- •Трёхшаговая аутентификация
- •Г.1. Аутентификация по протоколу оклик-отзыв
- •Г.2. Аутентификация с помощью кода аутентичности сообщения
- •Д.1. Дискретный логарифм
- •Д.2. Формирование общего ключа симметричного шифрования
- •Д.3. Уязвимость алгоритма Диффи-Хеллмана к атаке «человек посередине»
- •Контрольные вопросы
- •Принятые сокращения
- •Литература
4.4. Обнаружение ошибок с помощью избыточного циклического кода
Ниже приводятся три способа описания определения кода CRC: с использованием арифметики по модулю 2, с использованием полинома и аппаратная реализация [13].
4.4.1. Пример с использованием арифметики по модулю 2
В вычислениях по модулю 2 используется двоичное сложение без переноса в старший разряд (операция исключающего ИЛИ).
Введем следующие обозначения:
T – n-битовый кадр, который необходимо передать;
D – k-битовый блок сообщения (k первых бит кадра T);
R – (n-k) – битовая контрольная последовательность кадра (последние (n-k) бит кадра T). Значение R необходимо вычислить;
P - (n-k+1) – битовый делитель.
Пример:
Поскольку деление не дало остатка, считается, что ошибки отсутствуют. |
4.4.2. Пример с использованием полинома
Используя предыдущий пример, получаем: последовательности D = 1010001101 соответствует полином D(Χ) = Χ9 + Χ7 + Χ3 + Χ2 + 1, последовательности Р = 110101 - полином P(Χ) = Χ5 + Χ4 + Χ2 + 1, последовательности R = 01110 − R(Χ) = Χ3 + Χ2 + Χ.
Полиномиальное деление, соответствующее приведенному ранее двоичному делению, показано на рис. 4.9.
Ошибка не обнаружится только в том случае, если соответствующий полином Е(Х) делится на Р(Х). При надлежащем выборе полинома Р(Х) выявляются такие ошибки:
все 1-битовые ошибки, если Р(Х) имеет более одного ненулевого члена;
все 2-битовые ошибки, если Р(Х) имеет делитель из трех членов;
любое нечетное количество ошибок, если в разложении Р(Х) по множителям: присутствует (X + 1);
любой пакет ошибок, длина которого не превышает n-k, или, эквивалентно, не превышает длину контрольной последовательности кадра.
Здесь Q(X) – полином от Q.
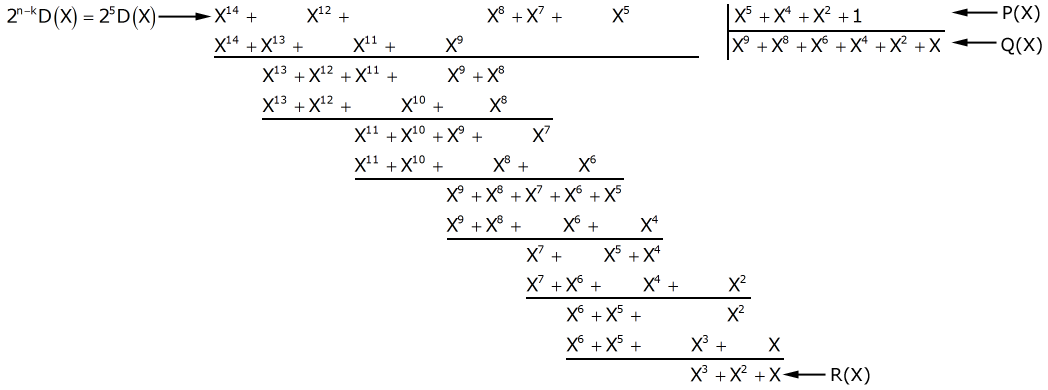
Рис. 4.9. Пример полиномиального деления
Приведем примеры длин n-k КПК (FCS) используемых полиномов Р(Х) в сетях связи: CRC – 3: в GSM. CRC – 16: в ОКС№7, X.25, Интернет (на межсетевом уровне, на транспортном уровне по протоколу TCP). CRC – 32: в ATM.
4.4.3. Пример аппаратной реализации
Процесс циклической проверки четности с избыточностью можно представить как схему деления, состоящую из элемента исключающего ИЛИ (сложение по модулю 2) и регистра сдвига. Регистр сдвига представляет собой строку 1-битовых ячеек памяти. Каждая ячейка имеет выходную шину, показывающую текущее хранимое значение, и входную шину. В дискретные моменты времени, которые называют тактами, значения ячеек памяти замещаются значениями, указанным во входной шине. Замена происходит синхронно во всем регистре, так что в результате значения ячеек регистра сдвигаются на один бит.
Реализация схемы выглядит следующим образом.
Регистр, содержащий (n - k) бит (по размеру контрольно-проверочной комбинации).
До (n - k) элементов исключающего ИЛИ.
Наличие или отсутствие логического элемента соответствует наличию или отсутствию члена в полиноме-делителе Р (Х), исключая члены 1 и Χn-k .
Понять архитектуру схемы деления можно с помощью примера, приведенного на рис. 4.10. В примере, как и выше, используются такие величины:
сообщение D = 1010001101; D(Χ) = Χ9 + Χ7 + Χ3 + Χ2 + 1;
делитель P = 110101; P(Χ) = Χ5 + Χ4 + Χ2 + 1.
На рис. 4.10, а) представлена реализация регистра сдвига. Процесс начинается с очистки регистра (все ячейки обнуляются). После этого передаваемое сообщение (делимое) побитово вводится в регистр, начиная со старшего бита. На pис. 4.10, б) приведена таблица, которая иллюстрирует пошаговую работу схемы по мере введения отдельных битов. Строки таблицы содержат значения пяти ячеек регистра сдвига в соответствующие моменты времени. Кроме того, в строках таблицы приводятся значения на выходе трех схем исключающего ИЛИ. Последнее число в каждой строке - значение следующего входного бита, который станет доступен для работы на следующем этапе.
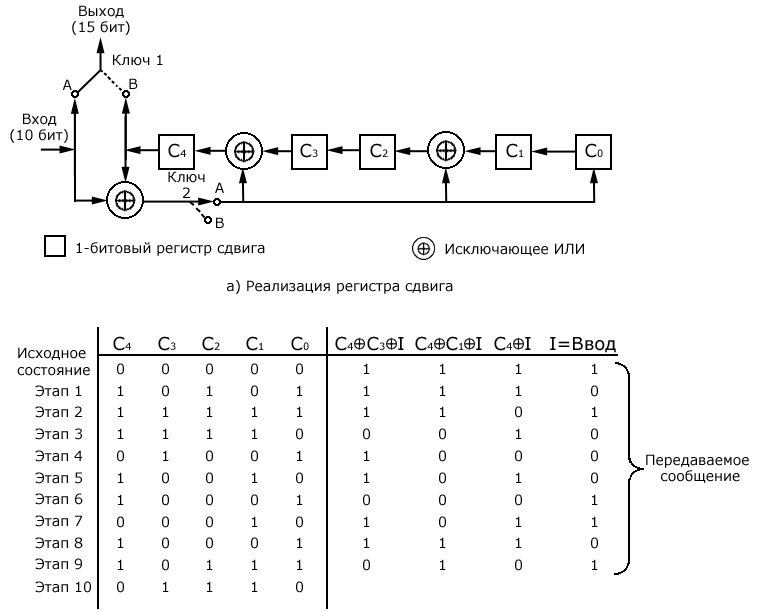
Рис. 4.10. Схема реализации аппаратным способом
Отметим, что операция исключающее ИЛИ влияет на значения ячеек С4, С2 и С0 при следующем сдвиге, что идентично рассмотренному ранее процессу двоичного деления. Процесс выполняется для всех битов передаваемого сообщения. Для обеспечения корректности выходного сигнала используются два ключа. При вводе битов данных оба ключа находятся в положении А. В результате за первые 10 шагов входные биты подаются в регистр сдвига и также используются в качестве выходных битов. По окончании обработки последнего бита данных регистр сдвига содержит остаток деления - содержание регистров после этапа 10. При вводе последнего бита данных в регистр оба ключа устанавливаются в положение В. В этом случае:
все логические элементы больше не изменяют значения битов;
за следующие 5 шагов на выход подаются 5 бит контрольно-проверочной комбинации (т.е. содержимое регистров после этапа 10).
В приемнике используется аналогичная логика. Принятые биты последовательности М вводятся в регистр сдвига по мере поступления. Если ошибки отсутствуют, то после обработки М регистр сдвига будет содержать последовательность контрольно-проверочной комбинации КПК. После этого начинает поступать переданная последовательность КПК.
В результате на выход регистра будут подаваться двоичные нули и по завершении приема все ячейки будут иметь значение 0.

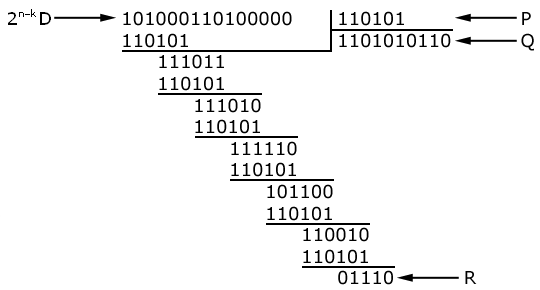 Здесь Q – целое число от деления.
Здесь Q – целое число от деления.