Д.1. Дискретный логарифм

В основу алгоритма Диффи-Хеллмана положена трудность вычисления дискретных логарифмов. Определим понятие дискретного логарифма.

Сначала определяется первообразный корень простого числа , как число, степени которого по модулю 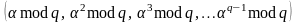, составляют полный набор целых чисел от 1 до (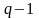 ). Например, если первообразный корень 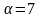, а , тогда для полного набора от 1 до 10 (т.е. ) 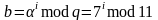принимает значения от 1 до 10.

В нижеследующей таблице приведены результаты вычислений, подтверждающие то, что - первообразный корень числа .

	1	2	3	4	5	6	7	8	9	10
	7	5	2	3	10	4	6	9	8	1

С целью упрощения вычислений воспользуемся следующим правилом арифметики в остаточных классах (классах вычетов)

Показатель степени называется дискретным логарифмом. При больших значениях первообразного корня и простого числа (порядка 512бит) по известному значению 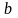вычисление дискретного логарифма становится практически неразрешимой задачей.

Д.2. Формирование общего ключа симметричного шифрования

На рис. Д.1 приведено формирование общего ключа симметричного шифрования.

Рис. Д.1. Формирование общего ключа

симметричного шифрования

Как видно из рис. Д.1., пользователь А определяет параметры и первообразный корень простого числа . Оба эти числа в открытом виде отправляют пользователю 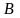в сообщении 1. На накладывается условие: (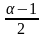 ) должно быть простым числом. Кроме этого на накладываются некоторые дополнительные условия. Значения и могут быть определены пользователем и в открытом виде отправлены пользователю .

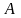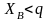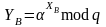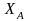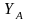Пользователь выбирает случайное целое число и вычисляет открытый ключ . Аналогично пользователь B выбирает случайное целое число и вычисляет открытый ключ . Значения и являются большими числами (например, 512-разрядными), и они сохраняются пользователями в секрете. Значения и 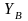(открытые ключи) свободно доступны другой стороне и поэтому передаются в сообщениях 1 и 2. Пользователь вычисляет общий ключ 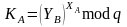, а пользователь по формуле .

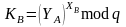Покажем, что оба ключа и 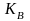равны. Воспользуемся для этого арифметикой в остаточных классах.

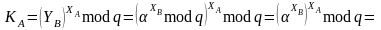
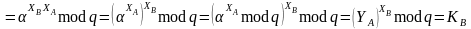
Таким образом, у пользователей и общий секретный ключ .

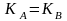Как видно из рис. Д.1, хотя величины , и известны (из сообщения), злоумышленнику вычислить дискретный логарифм из на сегодняшний день практически невозможно. Поэтому оказывается невозможным злоумышленнику вычислить общий секретный ключ .

Аналогично злоумышленнику невозможно вычислить дискретный логарифм из (при известных значениях , , ). Поэтому оказывается невозможным вычислить общий секретный ключ .

Пример

Для иллюстрации формирования общего секретного ключа с помощью алгоритма Диффи-Хеллмана выберем нереально небольшие значения и .

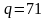Пользователи A и B выбирают также нереально небольшие значения и .

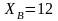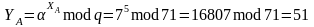
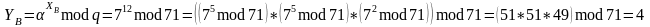
Производится обмен значениями и между пользователями.

Определяем значения ключей и .

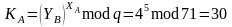
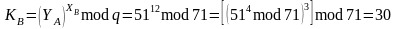
Таким образом, независимо друг от друга пользователи А и В определили общий секретный ключ .

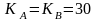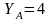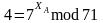Пользователь В получает сообщение 1 со значениями , и . Злоумышленнику путем полного перебора для таких небольших чисел удастся определить дискретный логарифм из выражения (т.е. ). Для значений , , , в несколько сотен бит каждый, эта задача определения неразрешима.