А.3. Метод количественной оценки угрозы безопасности сети связи
Согласно Рекомендации МСЭ-Т Е.408 [111] по требованиям к безопасности сетей электросвязи характеристика риска ИБ определяется двумя показателями – вероятностью угрозы безопасности и последствием ее воздействия при атаке злоумышленника (реализации этой угрозы).
Приведем метод количественной оценки угрозы информационной безопасности сети связи, изложенный в документе ETSI ETR 332 [112]. В некоторых документах количественную оценку угрозы информационной безопасности называют риском. В этом методе предлагается общая методология для всех систем сетей связи и заключается в следующем:
проводится оценка вероятности реализации угрозы Р;
определяется оценка последствий реализации угрозы G;
рассчитывается произведение P*G;
cоставляется ранжированный по этим произведениям список количественных оценок угроз. Согласно документу ETSI ETR 332 может быть использовано четыре оценки угрозы — высокая, средняя, низкая или незначительная.
Все приведенные выше параметры определяются экспертным способом и требуют высокой квалификации и опыта экспертов.
По данным в работе [113] по оценке аналитиков суммарные финансовые потери из-за угроз ИБ составляют от 1% до 5% валового дохода оператора связи. При этом отмечается, что операторы связи стараются не предоставлять сведений о масштабах потерь. При больших доходах они допускают небольшой процент потерь, считая их такими же неизбежными издержками бизнеса, как налоги.
Приложение б. Шифрование с общим ключом
Одним из основных механизмов обеспечения конфиденциальности данных является шифрование открытого текста. Наука о шифровании/дешифровании называется криптографией (cryptography). Результат шифрования сообщения P, который обозначим через C, образуется с помощью функции Ek, параметром которой является ключ K (т.е. C = Ek(P)). Особенность такой записи состоит в том, что параметр K записан не в виде аргумента функции E, а в виде нижнего индекса. Модель процесса шифрования/дешифрования показана на рис. Б.1.
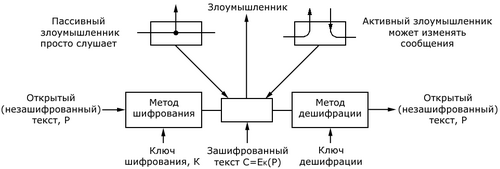
Рис. Б.1. Модель процесса шифрования/дешифрования
Предполагается, что противник или злоумышленник слышит и аккуратно копирует весь зашифрованный текст. Однако в отличие от получателя, которому предназначается данное сообщение, злоумышленник не знает ключа дешифрации, и поэтому расшифровка сообщения представляет для него большие трудности, или она просто невозможна. Иногда злоумышленник может не только прослушивать канал связи (пассивный злоумышленник), но способен также записывать сообщения и воспроизводить их позднее, вставлять свои сообщения или модифицировать исходное сообщение. Искусство взлома шифров называется криптоанализом.
Б.1. Классификация методов шифрования
На рис. Б.2. приведена классификация методов шифрования сообщений. Различают 2 типа алгоритмов шифрования/дешифрования: симметричное (его называют также традиционное или шифрование с общим ключом) и ассиметричное (его называют также шифрование с открытым ключом). Соответственно и криптография называется симметричной и асимметричной.
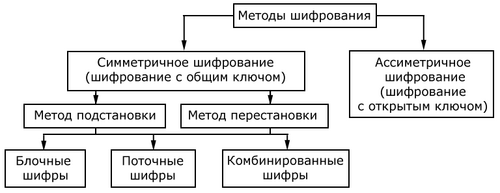
Рис. Б.2. Классификация методов шифрования сообщений
К основному принципу криптографии относится ограничение времени использования одного и того же ключа до минимума путём его частой смены. В криптографии принять считать, что противник может знать используемый алгоритм шифрования, перехваченный шифротекст, но не знает секретный ключ. Это называется правилом «Кирхгоффа».
Настоящая глава посвящена симметричному шифрованию, при котором ключ дешифрования совпадает с ключом шифрования. При дешифрации открытый текст P определяется с помощью функции дешифрования Dk, т.е. P = Dk (C). Подставив зашифрованное значение C в эту формулу, получаем, что P = Dk (Ek (P)). Основное правило криптографии состоит в предположении, что криптоаналитику (взломщику кода) известен используемый алгоритм шифрования. Другими словами, злоумышленник точно знает, как работает алгоритм шифрования Ek.
Из-за усилий, необходимых для разработки, тестирования и установки нового метода, каждый раз, когда старый алгоритм оказывался известным или считался скомпрометированным, хранить секрет шифрования просто непрактично. А предположение, что алгоритм остаётся секретным, когда это уже не так, могло бы причинить больший вред. Здесь на помощь приходит ключ шифрования. Ключ состоит из относительно короткой строки, определяющей один из огромного количества вариантов результата шифрования. В отличие от самого метода шифрования, который может изменяться только раз в несколько лет, ключ можно менять так часто, как это нужно.
Секретности алгоритма не стоит придавать большого значения. Попытка сохранить алгоритм в тайне обречена на провал. К тому же, опубликовав свой алгоритм, разработчик получает бесплатную консультацию от большого количества учёных-криптоаналитиков, горящих желанием взломать новую систему и тем самым продемонстрировать свои ум и учёность. Если никто не смог взломать алгоритм за 5 лет с момента его опубликования, то, по-видимому, этот алгоритм достаточно прочен. Поскольку реально в тайне хранится только ключ, основной вопрос заключается в его длине. Рассмотрим простой кодовый замок. Его основной принцип состоит в том, что вы последовательно вводите десятичные цифры. Все это знают, но ключ хранится в секрете. Ключ длиной в две цифры образует 100 вариантов. Ключ длиной в три цифры означает 1000 вариантов, а при длине ключа в шесть цифр число комбинаций достигает миллиона. Чем длиннее ключ, тем выше показатель трудозатрат взломщика кода. При увеличении длины ключа показатель трудозатрат для взлома системы путём простого перебора значений ключа растёт экспоненциально. Секретность передаваемого сообщения обеспечивается мощным (но всё же открытым) алгоритмом и длинным ключом. Чтобы не дать прочитать свою электронную почту, может быть достаточно 64-разрядного ключа. В коммерческих системах имеет смысл использовать 128-битный код.
С точки зрения криптоаналитика задача криптоанализа имеет 3 варианта. Во-первых, у криптоаналитика может быть некоторое количество зашифрованного текста без соответствующего открытого текста. Во-вторых, у криптоаналитика может оказаться некоторое количество зашифрованного текста и соответствующего ему открытого текста. В этом случае мы имеем дело с проблемой известного открытого текста. Наконец, когда у криптоаналитика есть возможность зашифровать любой кусок открытого текста по своему выбору, мы получаем третий вариант проблемы дешифрации, то есть проблему произвольного открытого текста. Если бы криптоаналитикам было позволено задавать вопросы типа: «Как будет выглядеть зашифрованное ABCDEFGHJKL?», задачи криптоаналитика решались бы легко. Новички в деле криптографии часто полагают, что шифр является достаточно надёжным, если он может выдержать атаку первого типа (только зашифрованный текст). Такое предположение весьма наивно. Во многих случаях криптоаналитик может угадать часть зашифрованного текста. Например, первое, что криптоаналитик получит несколько соответствующих друг другу пар кусков зашифрованного и открытого текста, его работа становится значительно легче. Для обеспечения секретности нужна предусмотрительность криптографа, который должен гарантировать, что система не будет взломана, даже если его оппонент сможет закодировать несколько участков открытого текста по выбору.