23.1.2.1. Метод перескока частоты

Для повышения устойчивости к узкополосным помехам в EDGE используется расширение спектра методом перескока частоты FHSS (Frequency Hopping Spread Spectrum). При этом доступная полоса частот разбивается на много каналов с меньшими полосами, разделенными защитными интервалами. Передатчик и приёмник используют один из этих каналов на протяжении некоторого времени, а затем производится перескок на другой канал. Схема использования отдельных каналов называется последовательностью перескоков. Время, на протяжении которого используется канал с определенной частотой, называется временем пребывания.

На рис. 23.2 приведён пример системы FHSS, на котором показано пять бит полезных данных, каждый продолжительностью t_b. Работая по схеме с медленным перескоком, передатчик использует частоту f2 на протяжении времени пребывания t_d, необходимого для передачи первых трех битов. Затем передатчик перескакивает на следующую частоту f3.

На рис. 23.3 и 23.4 приведены упрощенные структурные схемы передатчиков и приемников, работающие по технологии FHSS. На первом этапе передатчик схемы FHSS осуществляет модуляцию передаваемых данных согласно одной из схем цифро-аналоговой модуляции. В качестве примера можно взять схему частотной модуляции FSK (Frequency Shift Keying).

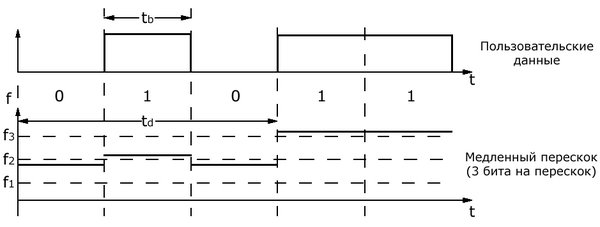
Рис. 23.2. Система FHSS

модуляции). Пусть по схеме FSK для двоичного нуля используется частота f₀, а для двоичной единицы - частота f₁. В результате формируется узкополосный модулирующий сигнал. На следующем этапе выполняется перескок частоты в соответствии с установленной последовательностью перескоков. Сведения о последовательности перескоков направляются в синтезатор частот, генерирующий несущие частоты f_i. При второй модуляции модулирующий узкополосный сигнал накладывается на несущую частоту и формируется новый расширенный сигнал. При этом нулю соответствует частота f_i + f₀, а единице – частота f_i+f₁. Если различные передатчики схемы FHSS используют только неперекрывающиеся последовательности перескоков, т.е. никогда не работают на одинаковой частоте в одно и то же время, то их передачи не мешают друг другу. Такой подход требует координации работы всех передатчиков и согласования их последовательностей перескоков.

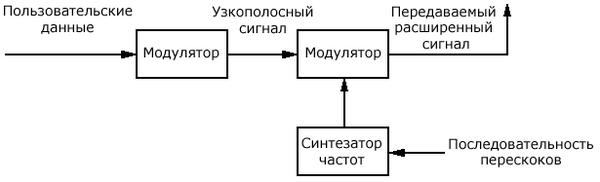
Рис. 23.3. Схема устройства передатчика, работающего по технологии FHSS

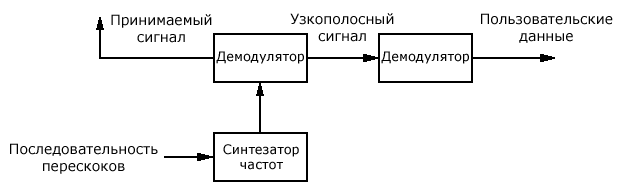
Рис. 23.4. Схема устройства приёмника, работающего по технологии FHSS

Приемник системы FHSS должен знать используемую последовательность перескоков. Кроме того, он должен постоянно поддерживать синхронизацию с передатчиком. При приеме выполняются действия, обратные процедуре модуляции, в результате чего передаваемые данные восстанавливаются. Кроме того, необходимо использовать несколько фильтров (на упрощенной диаграмме рис. 23.4 они не показаны).

3. 23.2. Сети сотовой связи стандарта umts

   1. 23.2.1. Принцип работы cистемы cdma

В отличие от GSM, основанных на множественном доступе FDMA и TDMA, в основу стандартов сотовых сетей связи третьего поколения 3G положен множественный доступ с кодовым разделением каналов CDMA. Рассмотрим принцип действия CDMA. К каждому пакету данных перед его передачей добавляется уникальный код. Такой код используется на приемном конце для восстановления. Таким образом, CDMA дает возможность использовать одновременно одну и ту же частоту для разных соединений. Эти коды используются для разделения различных пользователей в кодовом пространстве. Главная задача найти «хорошие» коды и отделить нужный сигнал от шума, создаваемого окружением и сигналами между другими пользователями. В CDMA каждый битовый интервал разбивается на m периодов, называемых чипами (кодовыми последовательностями). Обычно битовый сигнал заменяется чиповой последовательностью из 64 или 128 бит. Чтобы передать бит, равный 1, станция посылает свою чиповую последовательность. Чтобы передать бит, равный 0, станция передает дополнение этой чиповой последовательности (т.е. все единицы меняются на нули, а нули -на единицы). Никаких других комбинаций передавать определенной станции не разрешается. Например, если передатчику А присвоена чиповая последовательность 010011, то передача бит со значением «1» передается кодом 010011, а бит со значением «0» - кодом 101100.

Таким образом, CDMA является одной из форм расширения спектра. В отличие от GSM, где расширение спектра осуществляется методом перескока частоты, в CDMA расширение спектра осуществляется методом прямой последовательности DSSS (Direct Sequence Spread Spectrum). В CDMA расширение спектра служит для увеличения эффективной пропускной способности. Если имеется полоса шириной 1МГц, на которой работают 100 пользователей, то все пользователи используют всю ширину диапазона (1МГц) так, что чиповая скорость составляет 1Мчип/с.

Чипы пользователей подбираются таким образом, чтобы попарно были ортогональны, т.е. скалярное произведение двух чипов равно 0. Генерирование таких чиповых последовательностей осуществляется с помощью метода, известного как коды Уолша. Векторы (3,-2,4) и (-2,3,3) являются ортогональными: (3,-2,-4)* (-2,3,3) = -6-6+12=0. Однако векторы (1,2,3) и (4,2,-6)- неортогональны друг к другу (скалярное произведение равно -10), а векторы (1,2,3) и (4,2,-3) «почти» ортогональны (скалярное произведение равно -1), т.е. близко к нулю. Другим требованием к выбору чиповой последовательности является обладание хорошей автокоррекцией.

Объясним, что подразумевается под хорошей автокоррекцией. К примеру, код Баркера (+1,-1,+1,+1,-1,+1,+1,+1,-1,-1,-1) обладает хорошей автокоррекцией, т.е. его скалярный квадрат имеет большое значение, равное 11. При сдвигах кода Баркера на один или несколько чипов (представьте сдвиг 11-чипового кода Баркера относительно самого себя, повторенный несколько раз) абсолютная величина корреляции (скалярное произведение) не превышает 1. Ее значение будет оставаться таким низким до тех пор, пока код опять точно не совместится сам с собой.

Пример сдвига кода Баркера на 4

+1	-1	+1	+1	-1	+1	+1	+1	-1	-1	-1	Код Баркера
-1	+1	+1	+1	-1	-1	-1	+1	-1	+1	+1	Сдвиг на 4
-1	-1	+1	+1	+1	-1	-1	+1	+1	-1	-1	скалярное произведение равно -1

Прежде, чем разбирать алгоритм работы, рассмотрим следующую аналогию. Представьте себе зал ожидания в аэропорту. Множества пар оживленно беседуют. Временное уплотнение можно сравнить с ситуацией, когда все люди находятся в центре зала и говорят по очереди. Частотное уплотнение мы сравним с ситуацией, при которой люди находятся в разных углах и ведут свои разговоры, которые не слышны другим. Это происходит одновременно, но независимо. Для CDMA лучше всего подходит сравнение с ситуацией, когда все в центре зала, однако каждая пара говорящих использует свой язык общения. Франкоговорящие промывают косточки всем остальным, воспринимая чужие разговоры, как шум. Таким образом, ключевой идеей CDMA является выделение полезного сигнала при игнорировании всего остального. Далее следует упрощенное описание технологии CDMA.

Основы функционирования схемы CDMA можно объяснить с помощью следующих примеров.

Двум передатчикам, А и В, необходимо передать данные. Схема CDMA присваивает им следующие ключевые последовательности: ключ Аk =010011 и ключ Вk =110101. Передатчику А нужно послать бит Аd = 1, передатчику В – бит Bd= 0. В этом примере удобно кодировать бинарный ноль как -1, а бинарную единицу как +1. В результате Аd =+ 1, Bd= -1. Тогда к ним можно применять обычные правила сложения и умножения. Оба передатчика расширяют свой сигнал, используя ключи в качестве чиповых последовательностей (здесь термин «расширение» означает обычное умножение бита данных на всю чиповую последовательность). В действительности для расширения к отдельным битам данных применяются части намного большей чиповой последовательности.

Убедимся, что оба чипа ортогональные.

Ак	-1	+1	-1	-1	+1	+1
Вк	1	+1	-1	+1	-1	+1
Ак*Вк	-1	+1	+1	-1	-1	+1	0

Как видно, скалярное произведение Ak и Bk равно нулю. Передатчик А посылает сигнал As =Ad *Ak = +1 * (-1, +1, -1, -1, +1,+1) =(-1,+1, -1, -1, +1, +1). Передатчик В для расширения своего сигнала производит те же действия, но со своим кодом: Bs = Bd * Bk = -1 * (+1, +1, -1, +1, -1, +1) = (-1, -1, +1, -1, +1, -1).

Затем оба сигнала одновременно передаются на одинаковой частоте, поэтому в пространстве они накладываются друг на друга. Если интенсивность сигналов при приеме одинакова, а влиянием остальных передатчиков и шумом окружающей среды можно пренебречь, то приемник получит следующий сигнал С=Аs + Bs =(-2, 0, 0, -2, +2, 0). Допустим приемнику необходимы данные передатчика А и он настраивается на код А. Иначе говоря, для сужения применяется код передатчика А: С*Ак = (-2, 0, 0, -2, +2, 0) * (-1, +1, -1, ¬1, +1, +1) = 2 + 0 +0 + 2 + 2 + 0 = 6. Поскольку рузультат намного превышает 0, приемник детектирует бинарную единицу. При настройке на передатчик В, т.е. при использовании кода В приемник получит сигнал С*Вк = (-2, 0, 0, -2, +2, 0) * (+1, +1, -1, +1, -1, +1,) = - 2 + 0 + 0 – 2 – 2 + 0 = - 6. Результат отрицательный, поэтому детектируется бинарный ноль.

В этом примере было сделано несколько упрощений. Коды были очень простыми, но, по крайней мере, ортогональными. Что более важно, шумы считались пренебрежительно малыми, хотя в действительности шумы могут существенно влиять на передаваемый сигнал С. Соответственно, полученные результаты (+6, -6) могут оказаться не столь хорошими, а, например, близкими к нулю. В этом случае решить, что представляет собой сигнал – 0 или 1, - будет намного сложнее. Кроме того, интенсивность обоих принимаемых сигналов полагалась одинаковой. Однако, что произойдет, если интенсивность одного сигнала будет намного больше другого? Пусть, например, интенсивность сигнала в пять раз больше чем интенсивность сигнала А. Тогда С = As + 5*B = (-1, +1, -1, -1, +1, +1) + (-5, -5, +5, -5, +5, -5) = (- 6, - 4, + 4, - 6, + 6, -4). Допустим, что приемнику нужно получить данные передатчика В: С*Вк = - 6 – 4 – 4 -6 - 6 – 4 = -30. Бинарный ноль, посланный передатчиком В, легко детектируется. При приеме данных передатчика А сигнал будет выглядеть так: С*Ак = – 6 – 4 – 4 + 6 + 6 – 4 = 6. Понятно, что по абсолютной величине более сильный сигнал превосходит более слабый (+30 и +6). В то время как – 30 детектируется как бинарный ноль, для +6 принять решение не так легко: в сравнении с -30 значение +6 находится близко к нулю и поэтому может интерпретироваться как шум. Вспомним пример: если кто-то разговаривает на своем языке слишком громко, то использовать другой язык в качестве ортогонального кода бессмысленно – все равно вас никто не поймет, а слова лишь увеличат шум. При всей своей крайней упрощенности описанный пример указывает на то, что в системах CDMA необходим контроль мощности передачи. Это одна из крупнейших проблем, возникающих при использовании систем CDMA.

Уровни мощности, воспринимаемые приемником, зависят от того, насколько далеко находятся базовые станции. Уровни мощности контролируются базовыми станциями, выдающими сигнал увеличить или уменьшить.