Расчет пружины клапана

Выбор характеристики пружины

Пружина должна удерживать клапан в закрытом положении и обеспечивать кинематическую связь между движущимися деталями механизма в течение второго и третьего периодов движения, когда силы инерции клапана и других подвижных деталей стремятся оторвать толкатель от кулачка.

Плотная посадка клапана обеспечивается:

для выпускного клапана при

,

где − минимальное усилие пружины при закрытом клапане; − площадь горловины; и — давление газов соответственно в выпускном трубопроводе и в цилиндре при впуске. В бензиновых двигателях разность давлений ( ) достигает 0,05 − 0,07 МПа, а в дизелях − 0,02 − 0,03 МПа;

для впускного клапана в двигателях без наддува практически при любом минимальном усилии пружины, а в двигателях с наддувом при

,

где и − давление газов соответственно во впускном трубопроводе (давление наддува) и в цилиндре при выпуске.

Для обеспечения кинематической связи между деталями клапанного механизма необходимо, чтобы сила упругости пружины оставалась больше приведенной к клапану силы инерции механизма при движении толкателя с отрицательным ускорением на любом возможном скоростном режиме работы двигателя:

,,

где − коэффициент запаса, который учитывает возможность увеличения частоты вращения коленчатого вала двигателя от до 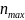, ограничиваемого регулятором или ограничителем частоты вращения, а также возможность вибрации пружины, при наличии которой сила может изменяться в значительных пределах (для дизелей при наличии механических центробежных регуляторов

k= 1,28 − 1,52, для бензиновых двигателей k=1,33 − 1,66); − приведенная к клапану сила инерции механизма при движении толкателя с отрицательным ускорением.

Усилие пружины будет минимальным, если на протяжении всего участка движения клапана с отрицательным ускорением коэффициент запаса остается постоянным.

Расчет пружины клапана сводится к выбору характеристики пружины, проверке ее минимального усилия при закрытых клапанах, выбору размеров пружины, определению ее запаса прочности и частоты собственных колебаний.

На рис. 7 представлен графический способ определения характеристики пружины.

Строят кривую подъема клапана и под ней кривую сил инерции поступательно движущихся масс на втором участке движения клапана. Задавшись необходимой величиной коэффициента запаса строят кривую силы пружины

,

направление которой противоположно силе инерции . Справа от кривой проводят вертикальную ось деформации пружины, а вправо от нее − горизонтальную ось силы пружины. Из точек , , проводят горизонтальные линии, на которых вправо от выбранной вертикальной оси откладывают соответствующие ординаты кривой .

Кривая, соединяющая полученные таким образом точки , представляет собой зависимость силы пружины от перемещения клапана, т. е. характеристику пружины, соответствующую постоянному значению коэффициента . Проведя через точки и прямую до пересечения с вертикальной осью (точка ), получают характеристику реальной пружины, обеспечивающей заданный коэффициент запаса в точках , кривой перемещения клапана. Отрезок, отсекаемый прямой на горизонтальной оси, соответствует силе пружины при закрытом клапане ( ), т. е. силе предварительной

з

11 грм

атяжки; отрезок, отсекаемый на вертикальной оси от точки

12 грм

до оси абсцисс, представляет собой деформацию пружины при закрытом клапане, а проекция прямой на вертикальную ось – максимальную деформацию пружины . На прямой к вертикали в масштабе диаграммы характеризует жесткость пружины .

В некоторых случаях выполнить условие равенства коэффициента запаса для начала и конца участка с отрицательным ускорением невозможно; например, в случае, когда закон движения клапана задан алгебраическим полиномом. В таких случаях обеспечивают необходимый запас силы пружины в начале участка с отрицательным ускорением, а характеристику пружины выбирают из условия получения приемлемых значений жесткости и максимальной силы. Следует иметь в виду, что при заданной максимальной силе наименьшие размеры пружины получаются в случае, когда .

В существующих двигателях это отношение находится в пределах 1,6 – 3,2.

Определение размеров пружины

Основными конструктивными параметрами цилиндрической пружины являются средний диаметр пружины , диаметр проволоки , число витков , шаг витка и полная длина свободной пружины. Средний диаметр , пружины выбирают из условий компоновки в зависимости от диаметра горловины:

.

Несмотря на различные размеры впускных и выпускных клапанов, пружины для всех клапанов принимаются одинаковыми.

При расчете пружины принимают, что сила направлена по оси пружины и создает скручивающий момент

M= .

ие кручения, вызываемое этим моментом, принимают равномерно распределенным по окружности сечения витка и определяют по формуле

13 грм

,

где − момент сопротивления кручению.

Для круглого сечения , следовательно,

.

В действительности напряжение распределяется по окружно­сти сечения витка неравномерно. Из-за кривизны витка наи­большее напряжение возникает в точках сечения, ближайших к оси пружины. Кроме того, сила вызывает срезывающее напряжение. Поэтому при определении напряжения в формулу вводят поправочный коэффициент 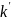, зависящий от отношения :

Тогда .

Для пружин с малым углом подъема витка (до 10°), к которым относятся клапанные пружины, коэффициент с достаточной точностью определяется по формуле

Задаваясь допустимым напряжением кручения в соответствии с прочностной характеристикой стали, выбранной для пружины, и коэффициентом , определяют диаметр проволоки:

.

Для пружинных сталей = 350 − 6ОО МПа. Коэффициентом задаются, исходя из предполагаемого отношения . Учитывая, что для большинства автомобильных двигателей оно укладывается в сравнительно узкие пределы (6 − 8), для которых соответственно =1,24 − 1,17, можно в качестве первого приближения принять, что . При этом формула принимает более простой вид

14 грм

.

Полученное значение округляют до ближайшего стандартного размера, уточняют отношение и коэффициент и определяют запас прочности пружины.

Значения коэффициента, учитывающего неравномерное распределение напряжений по поперечному сечению витка пружины:

3 4 5 6 7 8 9 10 11 12

1,5 1,38 1,3 1,23 1,2 1,17 1,15 1,13 1,11 1,1

Отношение для клапанных пружин можно принимать равным единице, так как концентрация напряжений, вызванная закручиванием витка, учитывается коэффициентом , а масштабный фактор для пружинной проволоки равен единице. Допустимое значение запаса прочности для автотракторных двигателей находится в пределах 1,2 − 1,4.

Число рабочих витков пружины определяют по максимальной деформации :

,

где модуль упругости второго рода, МН/см²;

– сила упругости пружины, МН; − соответственно средний диаметр, диаметр проволоки и максимальная деформация пружины, см.

Учитывая, что концевые витки, лежащие на тарелках или опорных поверхностях и частично прилегающие один к другому, при деформации не скручиваются, полное число витков 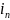принимают на 2 – 3 витка больше числа рабочих витков:

+(2 − 3).

Шаг витка выбирают с таким расчетом, чтобы при полностью открытом клапане между рабочими витками оставался зазор 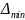=0,3 мм. Тогда шаг витка свободной пружины

+ .

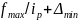Длина пружины при полностью открытом клапане

= .

15 грм

Длина пружины при закрытом клапане

= .

Длина свободной пружины

= .

При больших силах инерции каждый клапан оснащается двумя пружинами (наружной и внутренней). Усилия между пружинами распределяется следующим образом:

; .

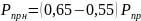Для обеспечения нормальных радиальных зазоров между направляющей втулкой и внутренней пружиной, а также между пружинами необходимо соблюдать условия (все размеры в мм):

; .

После определения размеров пружины ее обязательно следует проверить на резонанс. Колебания пружины не опасны в том случае, когда отношение низшей собственной частоты колебаний пружины не менее чем в 10 раз превышают частоту вращения распределительного вала:

.

Определения собственной частоты колебаний пружины, представляющей собой пространственный кривой брус, является весьма сложной задачей. Для упрощения ее решения пружину рассматривают как прямой брус, у которого длина, распределенная масса и жесткость равны соответственно длине, массе рабочих витков и жесткости пружины.

Частота собственных колебаний пружины

.

Диаметр проволоки и диаметр пружины следует подставлять в см.

При установке двух пружин должно соблюдаться неравенство .

16 грм

Определения собственной частоты колебаний пружины, представляющей собой пространственный кривой брус, является весьма сложной задачей. Для упрощения ее решения пружину рассматривают как прямой брус, у которого длина, распределенная масса и жесткость равны соответственно длине, массе рабочих витков и жесткости пружины.

Круговая собственная частота колебаний одноузловой формы пружины, определенная таким методом

,

где

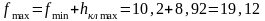
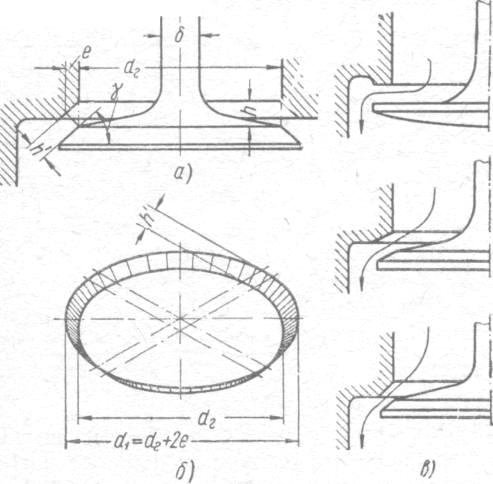
Рис. 1.Расчетная схема проходного

сечения в клапане

Рис. 2

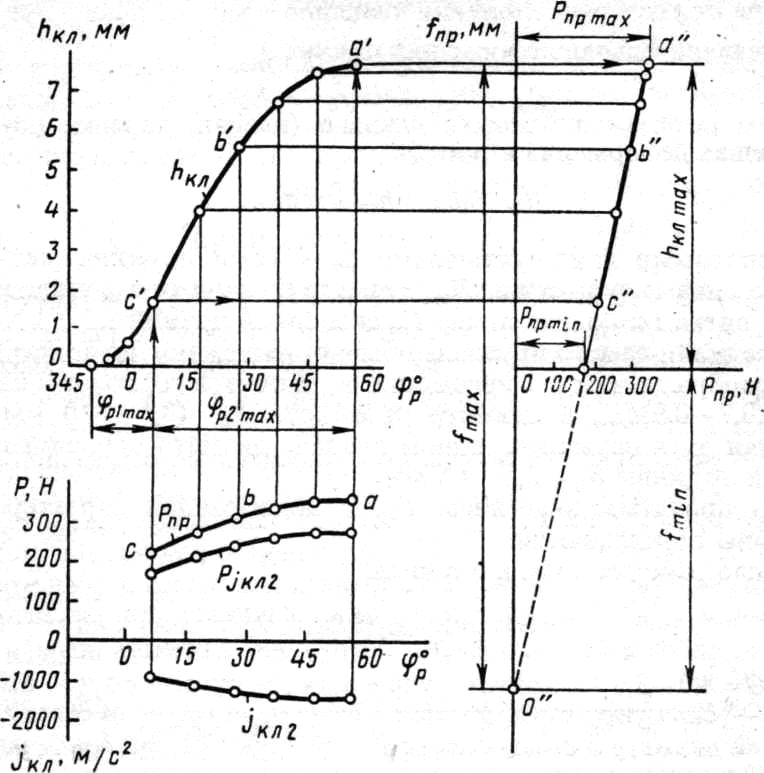
Рис. 2. Графическое построение

характеристики пружины

Рис. 7. Схемы приводов клапанов:

а – одноплечий рычаг; б – двуплечий рычаг

(коромысло)

1 грм