1.) Моделирование. Основные понятия.

Модель - это физический или абстрактный образ моделируемого объекта, удобный для проведения исследований и позволяющий адекватно отображать интересующие исследовате­ля физические свойства и характеристики объекта. Различают моделирование предметное и абстрактное. При предметном моделиро­вании - строят физическую модель, которая соответствующим образом отображает основные физические свойства и характеристики моделируемого объекта. При этом модель может иметь иную физическую природу в сравнении с моделируемым объектом. Если модель и объект од­ной и той же физической природы, то моделирование называют физическим. В этом случае модель может называться макетом. Абстрактное моделирование - связано с построением абстрактной модели. Такая мо­дель представляет собой математические соотношения, графы, схемы, диаграммы и т. п. Математическая модель - это совокупность математических объектов и соотношений между ними, адекватно отображающая свойства и поведение исследуемого объекта. Модель считается адекватной, если отражает исследуемые свойства с приемлемой точностью. Проведение исследований на та­кой модели называют вычислительным экспериментом. Алгоритм - это предписание, определяющее последовательность выполнения операций вычислительного процесса. Алгоритм, записанный в форме, воспринимаемой вычислительной машиной, представляет собой программную модель.

2.) Разновидности процессов подлежащих моделированию.

Все процессы делятся на детерменированные и стохастические. Детерминированными называются такие процессы, в которых отсутствуют случайные воздействия, динамика которых полностью определяется начальными условиями, и динамиче­ские переменные являются функциями времени. Поэтому динамику можно однозначно пред­сказать на основе изучения его механизма. Модели отображающие детерминированные про­цессы называются детерминированными моделями. Стохастическими процессами называются такие, параметры которых изменяются слу­чайно, под воздействием неконтролируемых дестабилизирующих воздействий, поэтому одно­значно предсказать поведение таких процессов на основе их изучения затруднительно; можно говорить лишь о вероятности того или иного типа их поведения. Модель такого тип называют стохастической. В соответствии с характером изучаемого процесса строятся жесткие или вероятностные модели. Жесткие (детерминированные) модели строятся обычно без использования статистиче­ских вероятностных распределений. В этом случае определенному значению входного пара­метра процесса соответствует вполне определенное значение его выходного параметра. Связь между входным и выходным параметрами в этом случае является функциональной связью. В случае статистической связи выходного параметра Yс входным X, каждому опреде­ленному значению X соответствует не определенное значение V (как в случае функциональной связи), а распределение значений Y, изменяющегося с изменением X. Поэтому вероятностные модели (когда решение принимается в условиях неопределенности) строятся с использовани­ем методов теории вероятностей и математической статистики.

3.) Иерархическое строение моделей.

На любом уровне иерархии исследуемый объект можно представить в виде некоторой системы, состоящей из элементов. В этой связи различают математические модели элементов и систем. При переходе к более высокому иерархическому уровню блочного структурированию система низшего уровня становится элементом системы нового уровня, и наоборот, при пере­ходе к низшему уровню элемент становится системой. В этом случае часто оказывается неце­лесообразным использование одних и тех же видов математических моделей на разных уров­нях. Обычно чем ниже уровень иерархии блочного структурирования объекта (например, тех­нического), тем более детальное описание его физических свойств. Следовательно, на низших уровнях используют наиболее сложные математические модели, На высших уровнях могут быть с успехом применены более простые модели. Их можно получить путем аппроксимации моделей низших иерархических уровней. При моделировании в новой области можно рекомендовать следующий подход к реше­нию задачи. На первом этапе следует создать “грубую” модель. Речь идет об учете только не­большого числа самых существенных факторов. Далее необходимо усовершенствовать эту самую грубую модель учетом некоторых факторов. Получив вторую модель, следует проверить, даст ли правиль­ный результат предельный подход к первой модели. Этот переход можно осуществить, если, например, устремить к нулю какой-либо параметр, значение которого связано с дополнитель­ным фактором, введенным во вторую модель. Таким же образом можно строить следующие модели. Например, в простейшем случае модель резистора можно описать одним параметром - сопротивлением R. Учет паразитной емкости и индуктивности в виде сосредото­ченных параметров дает следующий уровень модели, необходимой для адекватного модели­рования высокочастотных схем. Если изготовление резистора имеет какие-то особенности, то модель еще больше усложняется. Например, обобщенная эквивалентная схема замещения пленочного планарного резистора на ВЧ содержит 3 индуктивности и 5 емкостей (рис.) .

Ccex - внешние паразитные емкости на корпус контактных площадок на плате для поверхностно монтируемых резисторов; Cp - паразитные емкости резистора на корпус; Cs - паразитная последовательная емкость междуконтактами резистора; Lc - паразитные индуктивности контактов или выводов резистора; Ls – паразитная последовательная индуктивность резистора; R - активное сопротивление резистора. Метод последовательного усложнения модели введением дополнительных факторов или процессов может продолжаться до достижения необходимой адекватности модели. Именно так поступают на практике, постепенно переходя от простого к более сложному.В зависимости от степени абстрагирования при описании физических свойств техниче­ской системы различают три основных иерархических уровня: верхний или метауровень, сред­ний или макроуровень, нижний или микроуровень. Метауровень соответствует начальным стадиям проектирования, на которых осуществ­ляется научно-техничекский1 поиск и прогнозирование, разработка концепции и технического решения, разработка технического предложения. Для построения математических моделей ме­тауровня используют методы морфологического синтеза, теории графов, математической логи­ки, теории автоматического управления, теории массового обслуживания, теории конечных ав­томатов.На макроуровне объект рассматривается как динамическая система с сосредоточенными параметрами. Математические модели макроуровня представляют собой системы обыкновен­ных дифференциальных уравнений. Эти модели используют при определении параметров технического объекта и его функциональных элементов.На микроуровне объект представляется как сплошная Среда с распределенными пара­метрами. Для описания процессов функционирования таких объектов используют дифферен­циальные уравнения в частных производных. На микроуровне проектируют неделимые по функциональному признаку элементы технической системы, называемые базовыми элемента­ми. При этом базовый элемент рассматривается как система, состоящая из множества одно­типных функциональных элементов одной и той же физической природы, взаимодействующих между собой и находящихся под воздействием внешней Среды и других элементов техниче­ского объекта, являющихся внешней средой по отношению к базовому элементу.

4.) Математическое моделирование и математические модели.

Математическая модель - это совокупность математических объектов и соотношений между ними, адекватно отображающая свойства и поведение исследуемого объекта. Математическое отношение - это гипотетическое правило, связывающее два или более символических объекта. Математическая модель будет воспроизводить подходящим образом выбранные стороны физической ситуации, если можно установить правило соответствия, связывающее специфи­ческие физические объекты и отношения с определенными математическими объектами и от­ношениями. Математическое моделирование - метод качественного и (или) количественного опи­сания процесса с помощью, так называемой математической модели, при построении которой реальный процесс или явление описывается с помощью того или иного адекватного матема­тического аппарата. Математическое моделирование является типичной дисциплиной, находящейся, как сей­час часто говорят, на “стыке” нескольких наук. Адекватная математическая модель не может быть построена без глубокого знания того объекта, который “обслуживается” математической моделью. Иногда высказывается иллюзорная надежда, что математическая модель может быть создана совместно математиком, не знающим объекта моделирования, и специалистом по “объекту”, не знающим математики. Для успешной деятельности в области математического моделирования необходимо знать как математические методы, так и объект моделирования. С этим связано, например, наличие такой специальности как физик-теоретик, основной деятель­ностью которого является математическое моделирование в физике. Разделение специалистов на теоретиков и экспериментаторов, утвердившееся в физике, скорее всего, произойдет и в других науках, как фундаментальных, так и прикладных.

5.) Классификация математических моделей.

Классификация математических моделей на основе особенностей применяемого мате­матического аппарата. Математические модели с сосредоточенными параметрами. Обычно с помощью таких моделей описывают динамику систем, состоящих из дискретных элементов. С математи­ческой стороны - это системы обыкновенных линейных или нелинейных дифференциальных уравнений. Например, широко используется динамическая модель полупроводникового лазера. В этой мо­дели фигурируют две динамические переменные - концентрации неосновных носителей заряда и фотонов в активной зоне лазера. Математические модели с распределенными параметрами. Моделями этого типа описываются процессы диффузии, теплопроводности, распространения волн различной при­роды и т. п. В большинстве случаев математические модели электронных устройств являются моде­лями со сосредоточенными параметрами. Однако в некоторых случаях (например, при анализе процессов в длинных линиях, СВЧ-технике) используются модели с распределенными пара­метрами. В ряде случаев модели систем с распределенными параметрами строятся на основе компонентов со сосредоточенными параметрами. Примером может служить эквивалентная схема замещения длинной линии. Длинная линия - это электрическая линия, образованная двумя параллельными провод­никами тока, длина которых превышает длину волны передаваемых электромагнитных колеба­ний, а расстояние между проводниками значительно меньше длины волны. Длинная линия является системой с распределёнными параметрами, т.к. каждый элемент её длины обладает одновременно оперделенным значениями индуктивности L и активного со­противления R проводов, ёмкости С и проводимости тока G между проводами. Через эти па­раметры определяют основные характеристики длинной линии - волновое сопротивление Wи скорость распространения v электромагнитных волн вдоль неё.

В длинной линии без потерь R = G = 0 (обычно на радиочастотах). Остаются только L и C. Однако ни последовательное, ни параллельное соединение L и C не обеспечивает электриче­ских характеристик, свойственных длинной линии. Самая простая эквивалентная схема длин­ной содержит 3 индуктивности, 3 конденсатора и резистор. Математические модели, основанные на экстремальных принципах основываются на принципе наибольшего действия. получившего название метода наименьших квадратов (метод Гаусса), суть которого заключается в следующем. Пусть проводится опыт, целью которого является исследование зависимости некоторой физической величины Y от физической величины X. Предполагается, что величины х и у свя­заны функциональной зависимостью У=ф(х). Вид этой зависимости и требуется определить из опыта. Предположим, что в результате опыта получили ряд экспериментальных точек и построили график зависимости у от х. Обычно экспериментальные точки на таком графике располагаются не совсем правильно, дают некото­рый разброс, т. е. обнаруживают случайные отклонения от видимой общей закономерности. Эти отклонения связаны с неизбежными при всяком опыте ошибками измерения. Тогда возни­кает типичная для практики задача сглаживания экспериментальной зависимости. Для решения этой задачи обычно применяется расчетный метод, известный под названием метода наи­меньших квадратов (или метод Гаусса).

6.) Основной принцип классификации математических моделей.

В качестве основного принципа классификации математических моделей часто исполь­зуют области их применения. При таком подходе выделяются следующие области применения:

• физические процессы;

• технические приложения, в том числе управляемые системы, искусственный интеллект;

• жизненные процессы (биология, физиология, медицина);

• большие системы, связанные с взаимодействием людей (социальные, экономические,

экологические);

• гуманитарные науки (языкознание, искусство).

Области применения указаны в порядке, соответствующем убыванию уровня адекватно­сти моделей.

Классификация математических моделей (ТО - технический объект)

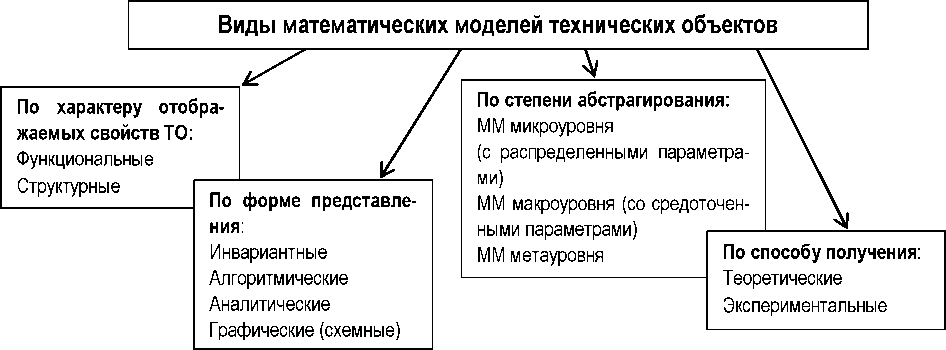
Структура модели - это упорядоченное множество элементов и их отношений. Параметр - это величина, характеризующая свойство или режим работы объекта. Выходные параметры характеризуют свойства технического объекта, а внутренние параметры - свойства его элемен­тов. Внешние параметры - это параметры внешней Среды, оказывающей влияние на функцио­нирование технического объекта.Функциональные модели описывают процессы функционирования технических объектов и имеют форму систем уравнений. Они учитывают структурные и функциональные свойства объекта и позволяют решать задачи как параметрического, так и структурного синтеза. Структурные модели отображают только структуру объектов и используются только при решении задач структурного синтеза. Параметрами структурных моделей являются признаки функциональных или конструктивных элементов, из которых состоит технический объект и по которым один вариант структуры объекта отличается от другого. Эти параметры называют морфологическими перемененными. Структурные модели имеют форму таблиц, матриц и гра­фов. Наиболее перспективно применение древовидных графов типа И-ИЛИ-дерева. Такие мо­дели широко используют на метауровне при выборе технического решения. В инвариантной форме математическая модель представляется системой уравнений вне связи с методом решения этих уравнений. В алгоритмической форме соотношения модели связаны с выбранным численным мето­дом решения и записаны в виде алгоритма - последовательности вычислений. Аналитическая модель представляет собой явные зависимости искомых переменных от заданных величин. Такие модели получают на основе физических законов, либо в результате прямого интегрирования исходных дифференциальных уравнений. Аналитические математи­ческие модели позволяют легко и просто решать задачи определения оптимальных парамет­ров Графическая (схемная) модель представляется в виде графов, эквивалентных схем, ди­намических моделей, диаграмм и т.п. Для использования графических моделей должно суще­ствовать правило однозначного соответствия условных изображений элементов графической и компонентов инвариантной математических моделей. В зависимости от степени абстрагирования при описании физических свойств техниче­ской системы различают три основных иерархических уровня: верхний или метауровень, сред­ний или макроуровень, нижний или микроуровень. Метауровень соответствует начальным стадиям проектирования, на которых осуществ­ляется научно-техничекский поиск и прогнозирование, разработка концепции и технического решения, разработка технического предложения. Для построения математических моделей ме­тауровня используют методы морфологического синтеза, теории графов, математической логи­ки, теории автоматического управления, теории массового обслуживания, теории конечных ав­томатов. На макроуровне объект рассматривается как динамическая система с сосредоточенными параметрами. Математические модели макроуровня представляют собой системы обыкновен­ных дифференциальных уравнений. Эти модели используют при определении параметров технического объекта и его функциональных элементов. На микроуровне объект представляется как сплошная Среда с распределенными пара­метрами. Для описания процессов функционирования таких объектов используют дифферен­циальные уравнения в частных производных. На микроуровне проектируют неделимые по функциональному признаку элементы технической системы, называемые базовыми элемента­ми. При этом базовый элемент рассматривается как система, состоящая из множества одно­типных функциональных элементов одной и той же физической природы, взаимодействующих между собой и находящихся под воздействием внешней Среды и других элементов техниче­ского объекта, являющихся внешней средой по отношению к базовому элементу. Теоретические модели получают на основе описания физических процессов функциони­рования объекта, а экспериментальные - на основе поведения объекта во внешней среде, рас­сматривая его как “черный ящик”. Эксперименты при этом могут быть физические (на техниче­ском объекте или его физической модели) или вычислительные (на теоретической математи­ческой модели).

7.) Программирование модели

Порядок действий: 1. Составляется план создания и использования программной модели. 2. Затем исследователь приступает к программированию модели. В качестве технического задания на программирование служит описание имитационной модели. Специфика работ по программированию модели зависит от средств автоматизации моделирования, которые дос­тупны исследователю. Для создания моделей электронных устройст существуют специализированные средства, в том числе и специализированные языки программирования (точнее, языки описания элек­тронных схем), в частности семейства SPICE (Simulation Program with Integrated Circuit Emphasis) — симулятор электронных схем общего назначения с открытым исходным кодом. Есть целый ряд специализированных программ схемотехнического моделирования, которые используют единый синтаксис SPICE (или его разновидности - PSPICE, HSPlCE, LTSPICE). Эти программы используются в разработке электронных устройств, интегральных схем, печатных плат, для проверки целостности схемы и для анализа ее поведения. После первичной отладки компонет модели переходят ко второму этапу: проверке досто­верности программы модели системы. После исключения грубых ошибок ряд блоков объединяется и начинается комплексная отладка модели с использованием тестов. Отладка по тестам начинается с нескольких блоков, затем в этот процесс вовлекается все большее число блоков модели. Следующим действием является составление технической документации на модель сложной системы. Для проверки адекватности модели объекту исследования после составления фор­мального описания системы исследователь составляет план проведения натурных экспери­ментов с прототипом системы. Если прототип системы отсутствует, то можно использовать систему вложенных ИМ, отличающихся друг от друга степенью детализации имитации одних и тех же явлений. Тогда более детальная модель служит в качестве прототипа для обобщенной ИМ. Если же построить такую последовательность невозможно либо из-за отсутствия ресурсов на выполнение этой работы, либо из-за недостаточности информации, то обходятся без про­верки адекватности ИМ. При обнаружении ошибок на этапе отладки, устранимых только на предыдущих этапах, может иметь место возврат на предыдущий этап.

8.) а) Испытание моделей. б) Исследование свойств имитационной моделей. в) Эксплуатация имитационной модели. г) Анализ результатов моделирования.

а) При этом необходимо выполнить следующее. Во- первых, убедиться в правильности динамики развития алгоритма моделирования объекта ис­следования в ходе имитации его функционирования (провести верификацию модели). Во- вторых, определить степень адекватности модели и объекта исследования. Под адекватностью программной имитационной модели реальному объекту понимают совпадение с заданной точ­ностью векторов характеристик поведения объекта и модели. При отсутствии адекватности проводят калибровку имитационной модели («подправляют» характеристики алгоритмов ком­понент модели).

Наличие ошибок во взаимодействии компонент модели возвращает исследователя к эта­пу создания имитационной модели.

б) При этом оцениваются точность имитации явлений, устойчивость результатов моделиро­вания, чувствительность критериев качества к изменению параметров модели. Получить эти оценки в ряде случаев бывает весьма сложно. Точность имитации явлений представляет собой оценку влияния стохастических элемен­тов на функционирование модели сложной системы. Устойчивость результатов моделирования характеризуется сходимостью контролируемо­го параметра моделирования к определенной величине при увеличении времени моделирова­ния варианта сложной системы. Стационарность режима моделирования характеризует собой некоторое установившееся равновесие процессов в модели системы, когда дальнейшая имитация бессмысленна, по­скольку новой информации из модели исследователь не получит и продолжение имитации практически приводит только к увеличению затрат машинного времени.

в) Этот этап начинается с составления плана эксперимента, позволяющего исследователю получить максимум информации при минимальных усилиях на вычисление. Обязательно ста­тистическое обоснование плана эксперимента. Планирование эксперимента представляет со­бой процедуру выбора числа и условий проведения опытов, необходимых и достаточных для решения поставленной задачи с требуемой точностью. При этом существенно следующее: стремление к минимизации общего числа опытов, обеспечение возможности одновременного варьирования всеми переменными; использование математического аппарата, формализую­щего многие действия экспериментаторов; выбор четкой стратегии, позволяющей принимать обоснованные решения после каждой серии экспериментов на модели. Затем исследователь приступает к проведению рабочих расчетов на модели. Это весьма трудоемкий процесс, требующий больших затрат ресурса ЭВМ и обилия канцелярской работы.

г) Данный этап завершает технологическую цепочку этапов создания и использования ими­тационных моделей. Получив результаты моделирования, исследователь приступает к интер­претации результатов. Здесь возможны следующие циклы имитации. В первом цикле имитаци­онного эксперимента в ИМ заранее предусмотрен выбор вариантов исследуемой системы пу­тем задания начальных условий имитации для машинной программы модели. Во втором цикле имитационного эксперимента модель модифицируется на языке моделирования, и поэтому требуются повторная трансляция и редактирование программы.

9.) Виды анализа и расчета электронных схем.

Расчет статического режима схемы выполняется для построения карты режимов по постоянному току, определения различных статических параметров, например, выделяемой на элементах мощности. Данный вид расчета используется для определения начальных условий для расчета переходных процессов и определения рабочей точки для расчета малосигнальных параметров.Расчет малосигнальных параметров схемы и расчет переходных процессов служит ос­новой для определения динамических параметров схемы. Позволяет сделать вывод о работо­способности схемы при различных входных воздействиях. Расчет выходных параметров схемы производят после расчета статического режима и переходных процессов. Это позволяет получить данные о соответствии или несоответствии внешних параметров схемы параметрам, указанным в ТЗ.

Анализ схемы предполагает:1.Анализ параметрической чувствительности, т.е. определение степени влияния из­менения внутренних параметров схемы на выходные параметры 2.Статистический анализ позволяет найти характеристики схемы при статистическом отклонении параметров элементов схем (внутренних параметров). В результате могут быть по­строены гистограммы выходных параметров, по которым могут быть определены границы от­браковки годных изделий.. 3.Анализ на наихудший случай - предполагает расчет выходных параметров схемы при наихудшем сочетании внутренних параметров схемы. 4.Анализ влияния внешней среды состоит в расчете влияния температуры, давления, влажности и т.п. на выходные параметры. Фактически, анализ выполняется в два этапа: вначале выясняются зависимости параметров компонентов электронной схемы от изме­нения внешней среды. 5.Многовариантный анализ представляет собой расчет схемы при различных комбина­циях параметров элементов, задаваемых проектировщиком, который проводится за одни сеанс расчета. В ряде случаев многовариантный анализ схемы позволяет обойтись без оптимизации параметров элементов схемы, поскольку разработчик получает результаты расчета совокупно­сти схем и может выбрать наилучший вариант.

10.) Общие принципы построения модели (эквивалентной схемы) для проведения анализа по постоянному току.

В режиме ОС рассчитываются передаточные характеристики по постоян­ному току. Ко входам цепи подключаются один или два независимых источника постоянного напряжения или тока. В качестве выходного сигнала может рассматриваться разность узловых потенциалов или ток через ветвть в которую включен резистор . При расчете режима ОС программа закорачивает ин­дуктивности, исключает из схемы конденсаторы и затем рассчитывает режим по постоянному току при нескольких значениях входных сигналов. Например, при подключении одного источника постоянного напряжения мо­жет рассчитываться передаточная функция усилителя, а при подключении двух источников — семейство статических выходных характеристик транзи­стора. Как правило, режим анализа ОС и используется в основном для этих двух целей: построения вольтамперных характеристик полупроводниковых и электронных приборов и снятия передаточных характеристик усилителей постоянного тока не содержащих реактивных компонентов.

11.)Общие принципы построения моделей(эквивалентной схемы) для проведения анализа по переменному току(частотного анализа).

АС-анализ –это малосигнальный или линейный анализ. При этом все переменные состояния схемы связаны между собой линейными зависимостями. Это значит, что, скажем, удвоение некоторого напряжения в схеме приводит к удвоению всех величин в схеме связанных с ним. При АС- анализе программа использует для всех компонентов схемы их малосигнальные линеаризованные модели- т.об. получается малосигнальная линеаризованная схема замещения всего устройства. Линеаризованная схема замещения описывается системой линейных алгебраических уравнений с комплексными (зависящими от частоты) коэф-ми. Наличие комплексных коэф-ов обусловлено инерционными компонентами, к-рые для электронных устройств представляют собой реактивные –емкостные и индуктивные элементы. При выполнении анализа программа решает указанную систему для всех частот в пределах заданного диапазона и выводят на экран зависимость заданных переменных состояния схемы от частоты.

Правила составления линеаризованных малосигнальных моделей.

12.)Классификация моделей компонентов электронных схем.

Математические модели технических устройств могут быть классифицированы по ряду признаков:

1. По характеру отображаемых процессов выделяют: статические и динамические модели.

2. По способу представления модели различают: аналитические, графические и

табличные

Аналитические модели определяют прибор или компоненту в виде уравнений, описы­вающих его ВАХ или в форме дифференциальных уравнений описывающих переходные про­цессы в моделируемой схеме и характеризующие инерционность элемента.

Графические модели позволяют представить компоненты в виде графиков ВАХ или в ви­де эквивалентных схем замещения.

Табличные модели позволяют представить схему или элемент в виде цифровых таблиц, полученных в ходе экспериментального исследования объекта моделирования и соответст­вующих графикам экспериментальных ВАХ. Табличные модели используют обычно в том слу­чае; если аналитическую модель построить трудно вследствие сложной зависимости. Иногда при сложных функциональных аналитических зависимостях для ВАХ их сознательно табули­руют, если это позволяет объем памяти ЭВМ, и создают таким образом, возможно менее точ­ную, но более удобную модель.

Перечисленные выше модели могут быть выполнены в виде подпрограмм, при таком представлении они превращаются в цифровую модель.

Аналитические и графические модели могут быть также заданы в виде алгоритма вычис­ления внешних параметров модели, при этом модель носит название алгоритмической модели. После оформления подпрограммы в соответствии с приведенным алгоритмом модель стано­вится цифровой.

Цифровые модели могут быть достаточно точными, т.к. степень их сложности в основном определяется сложностью программы и допустимыми для расчета затратами машинного вре­мени. В настоящее время цифровые модели используются все более широко в связи с разви­тием САПР РЭА.

3. По характеру зависимостей модели делятся на: линейные и нелинейные

Имеется особый класс кусочно-линейных моделей, нелинейность которых проявляется в ограниченном количестве точек стыка линейных участков.

Нелинейные модели, естественно, оказываются более точными, но и более сложными.

4. По диапазону рабочих сигналов модели классифицируются на: модели большого сигнала и малосигнальные

Малосигнальные модели, как правило, представляют собой линейные модели; модели для большого сигнала учитывают нелинейность характеристик активных и пассивных элемен­тов схемы (биполярных и полевых усилительных приборов).

5. По диапазону рабочих частот выделяют: низкочастотные, высокочастотные и

сверхвысокочастотные

Низкочастотные модели не учитывают инерционность компонентов модели и, поэтому низкочастотные модели используют для расчета схем по постоянному току (в статическом ре­жиме).

Высокочастотные модели — модели более высокого уровня, они учитывают помимо осо­бенностей статического режима инерционность компонентов. Поэтому такие модели дополня­ют системой дифференциальных уравнений, учитывающей инерционность компонентов, или эквивалентными схемами реальных приборов на высоких частотах — индуктивностями и емко­стями выводов, инерционностями, определяющими физические процессы в компонентах (на­пример, накопление заряда), емкостями областей структур и т.п.

Особенность низкочастотных и высокочастотных моделей состоит в том, что они выпол­няются на сосредоточенных элементах и поэтому для этих моделей справедливы законы Кирх­гофа.СВЧ модели отличаются от высокочастотных моделей учетом пространственных и вре­менных координат, поэтому для анализа и расчета СВЧ-схем необходимо использовать урав­нения Максвелла. Применение законов Кирхгофа оправдано лишь в диапазоне частот до 10 гГц, где размеры компонентов (особенно компонентов ИС) остаются меньше длины волны 1=3 см.

13.)Базовый набор элементов моделей.Зависимые и независимые источники тока и напряжения. Их основные параметры.

Существует ряд моделей, на основе которых может быть построена любая электрическая модель прибора. Эти модели получили название базового набора элементов моделей. Идеальные активные элементы – идеальные источники напряжения или тока - вводятся для характеристики реальных источников электрической энергии, в которых неэлектрические виды. Рис. 2.3. Независимый идеальный источник эдс энергии (химическая, механическая) преобразуются в электрическую. В зависимости от вида ВАХ и возможности управления выходными параметрами различают зависимые и независимые источники напряжения и тока. Независимый идеальный источник напряжения представляет собой двухполюсный элемент, напряжение на котором, возможно, изменяется во времени по некоторому закону e(t), не зависящему от величины тока, проходящего через источник. Выходная характеристика источника u(l), его эквивалентная схема замещения (рис. 2.3).В режиме короткого замыкания величина тока источника стремится к бесконечности, источник отдает бесконечно большую мощность в нагрузку. Независимый идеальный источник тока представляет собой двухполюсный элемент, выходной ток которого изменяется, возможно, по некоторому закону во времени независимо от напряжения на элементе. Источник отдает в нагрузку бесконечно большую мощность при холостом ходе. Эквивалентная схема и ВАХ источника изображены на рис. 2.4.

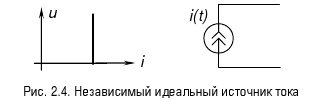
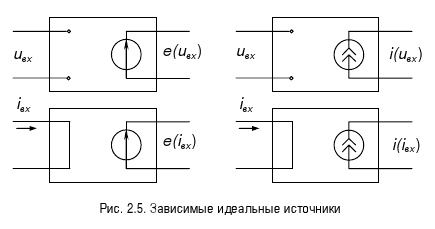
Зависимые идеальные источники напряжения или тока представляют собой трехполюс­ные или четырехполюсные элементы (необратимые), которые ставят в зависимость от входно­го сигнала (напряжения или тока) выходной ток или напряжение. Если управление зависимыми источниками осуществляется током, то его вход представляет собой короткое замыкание, если напряжением — холостой ход. Изображение зависимых источников напряжения или тока при­ведено на рис. 2.5:

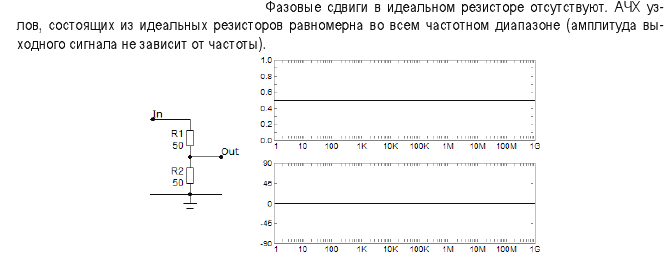
14.)Модели резистора. Идеальный линейный резистор характеризуется только одним параметром -сопротивлением R или проводимостью G. Проводимость - величина, обратная сопротивлению: G=1/R. Размерности ве­личин: R[Om], G[Cm], Сопротивление (проводимость) устанавливает связь между током через резистор и напряжением на нем: U=IR.

Рис. 1.1. ВАХ резистора: 1- линейного, 2 - нелинейного

В общем случае сопротивление резистора может быть посто­янным, либо меняться в зависимости от каких-либо воздействий (механических, температурных, электрических и т.д.). Если сопро­тивление не зависит от тока через резистор или напряжения на нем, то говорят, что оно нелинейно (зависимость тока от напряжения - прямая линия). В противном случае оно нелинейно. Нелинейное сопротивление характеризуется ВАХ (рис. 1.1). Компонент с такой характеристикой называется нелинейным резистором.

У реального резистора вольтамперная характеристика на постоянном токе не отличается от иде­альной. Однако любой реальный резистор помимо сопротивления обладает емкостью и индуктивно­стью. Эти дополнительные параметры резистора называются паразитными параметрам Такими пара­метрами обладает не только резистор, но и любой другой реальный компонент (конденсатор, катушка индуктивности, трансформатор, транзистор и т.д.). Величина паразитных параметров определяется в основном конструктивными особенностями компонента и при определенных условиях паразитные па­раметры компонентов могут оказывать существенное влияние на работу электронных схем. Поэтому при создании моделей компонентов (особенно предназначенных для работы на высоких частотах) не­обходимо предусмотреть возможность учета паразитных параметров. Это существенно усложняет мо­дели. Например, даже упрощенная высокочастотная модель резистора состоит из трех компонентов (рис. 1.8). Однако и она не в полной мере отражает поведение резистора во всей области частот. Эта модель использует сосредоточенные параметры (C и L), а на самом деле, они распределенные. Если же заменить сосредоточенные параметры распределенными, то модель еще более усложняется.На практике не всегда используют модели с полным набором параметров, поскольку учет всех па­разитных компонентов может существенно увеличить время расчета, а точность не повысится. Напри­мер, на частотах в единицы килогерц учет емкости и индуктивности пленочных резисторов нецелесообразен, поскольку на таких частотах реактивные свойства практически не проявляются. А вот учет индуктивности проволочного резистора уже обязателен, поскольку его паразитная индуктивность намного больше. В области СВЧ, при моделировании элементов в гибридном интегральном или твердотельном исполнении, необходимо ис­пользование самой сложной модели - с распределенными пара­ и метрами, поскольку в этих областях применения обязателен учет эффектов длинных линий.

На более низких частотах учитывают либо только индуктивность, либо емкость и индуктивность как сосредоточенные пара­метры. Индуктивность резистора формируется за счет индуктивности выводов и индуктивности резистив­ного слоя. В зависимости от технологии изготовления величина этого паразитного параметра может меняться в сотни раз и даже более. За счет наличия паразитной индуктивности (рис. 1.9) сопротивле­ние резисторов на высокой частоте становится комплексным, приобретает индуктивный характер:

Здесь первое слагаемое- активная составляющая полного сопротивления, второе- реактивное

20)определение параметров модели биполярного транзистора.

15. Модель конденсатора

16. Модель катушки индуктивности (дросселя)

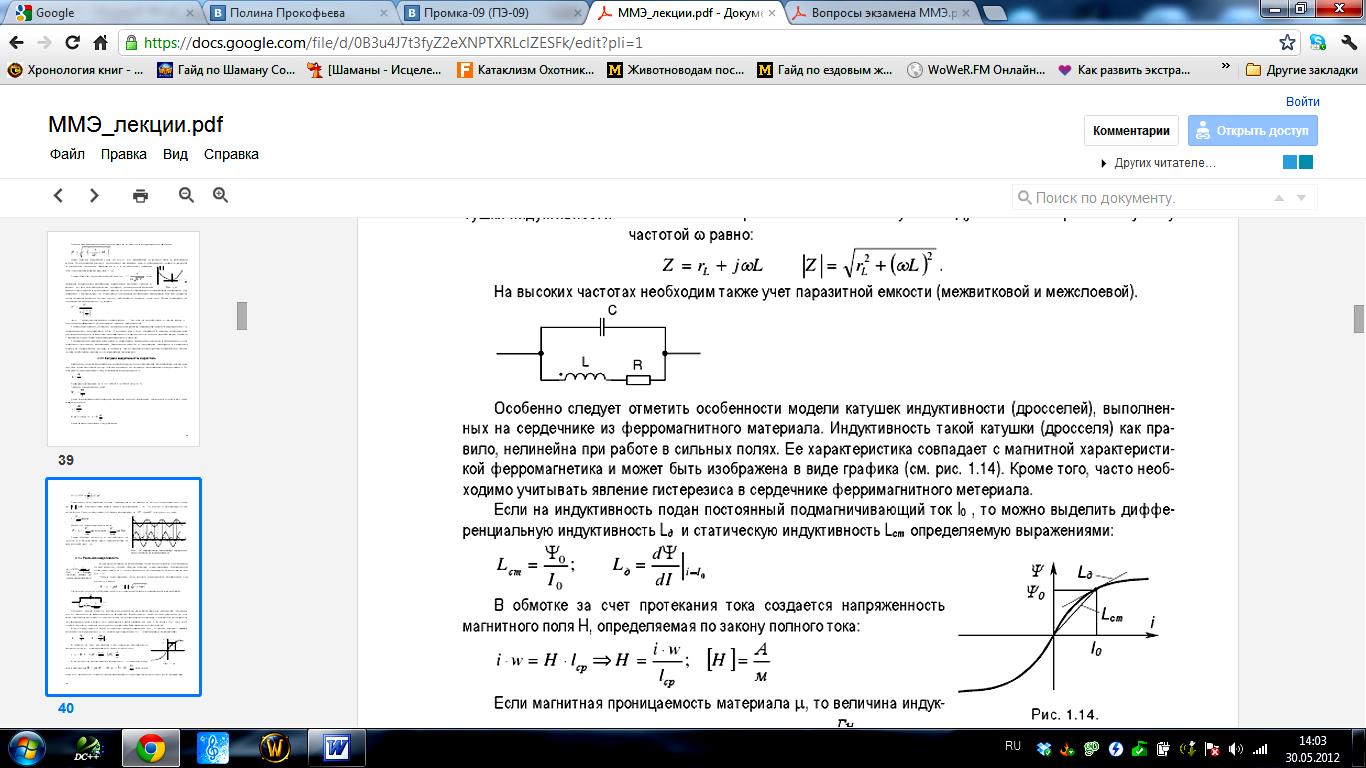
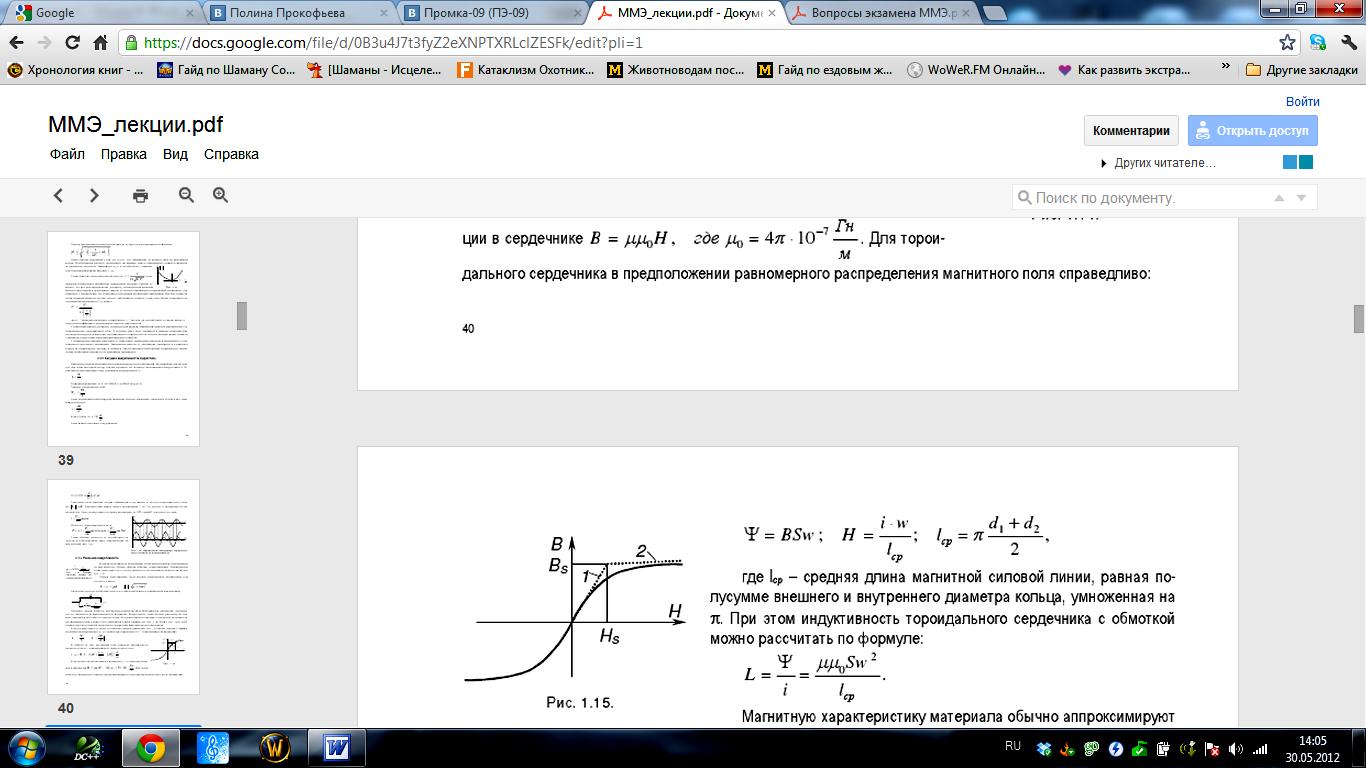
17. Модель трансформатора

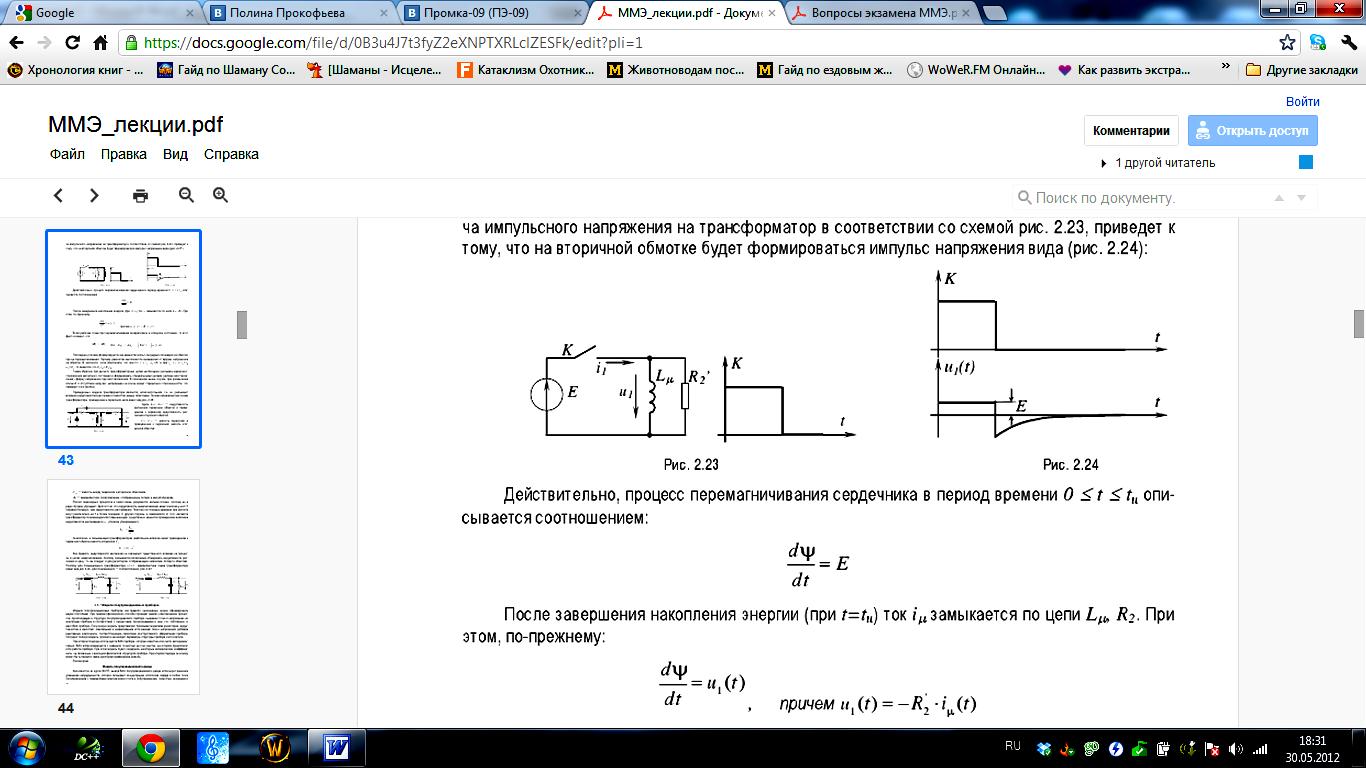
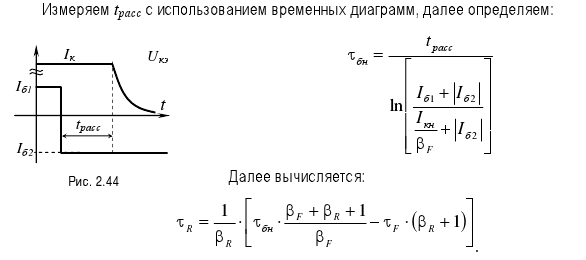
18.)Модель полупроводникового диода.

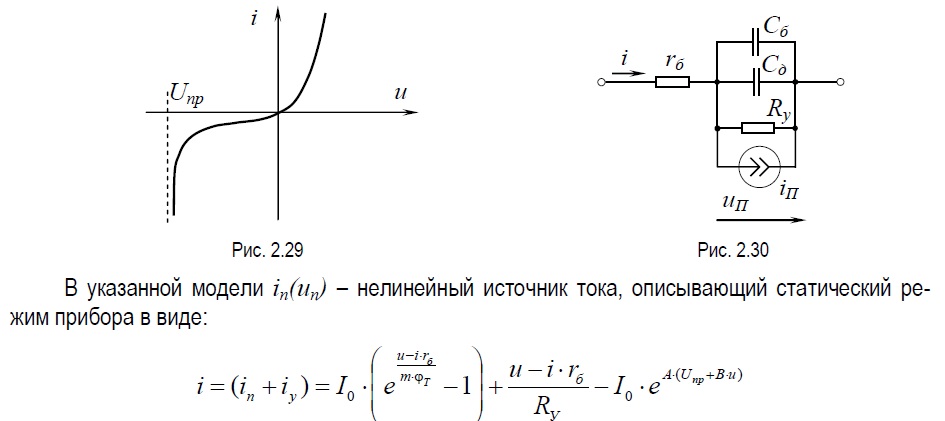
19.) Модель биполярного транзистора Эмберса-Мола

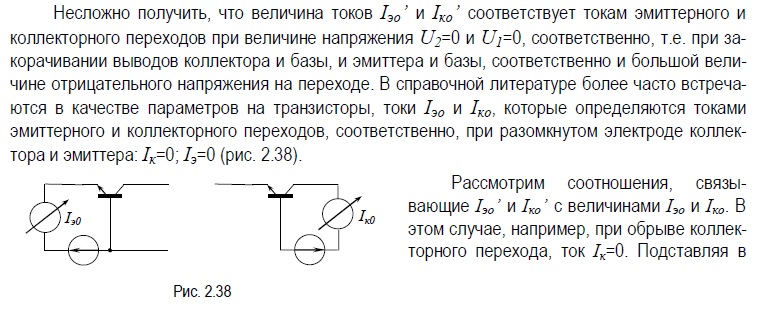
21.) Малосигнальная динамическая модель биполярного транзистора

Для активного нормального режима малого сигнала широко используется простая моди-

фикация модели Эберса-Молла, которая может быть получена из основной модели при учете:

а) прямого смещения эмиттерного перехода Uбэ>0;

б) большого отрицательного смещения на коллекторном переходе Uбк<0;

в) малого изменения напряжений и токов относительного рабочей точки по постоянному

току.

Рассмотрим для этого случая уравнения Эберса-Молла: