
- •Билет 1
- •Билет 2
- •Билет 3
- •Билет 4
- •Билет 5
- •Падений напряжений в нём. Действующеезначение Билет 6
- •1.Рух частинки в однорідному магнітному полі:
- •2.Основна задача електростатики провідників і доказ того, що вона має тільки один розв’язок
- •Билет 7
- •Термоэлектронная эмиссия
- •Билет 8 Напруженість електричного поля.
- •Билет 9
- •9.1.Уравнения Лапласа и Пуассона для скалярного потенциала.
- •2. Глибина проникнення змінного магнітного поля у речовину. Скін-ефект.
- •Билет 10
- •Билет 11
- •Закон Ома в интегральной форме
- •Закон Ома в дифференциальной форме
- •Билет 12
- •Билет 13
- •1. Сила электрического взаимодействия.
- •2.Плотность энергии магнитного поля
- •Билет 14
- •1. Квазистаціонарний струм.
- •Билет 15
- •Интегральная форма
- •Билет 16
- •1.Электромагнитные волны.
- •2 Дивергенції полів b і h, їх граничні умови.
- •Билет 17
- •Билет 18 Прості кола змінного струму
- •2.Рух зарядженоїчастинки в однорідних полях
- •Билет 19
- •Билет 20
- •Билет 22
- •2)Сила лоренца
- •Билет 23
- •Билет 24
- •Билет 25
- •Закон ампера
- •Билет 26
- •Вектор поинтинга
- •Билет 27
- •Аналоги законов кирхгофа и ома при расчете магнитных цепей
- •Билет 28
- •[Править]Вывод
- •Интерпретация
- •Билет 29
- •Первое уравнение максвела
- •Четвертое уравнение максвела
- •2) Типы магнетиков
- •Феромагнетики и их свойства
- •Билет 30
- •2) Магнитное поле токов
Билет 2
2.1)Пондеромоторные
силы. В электрических полях на
диэлектрики и проводники действуют
силы - пондеромоторные силы. Природа
сил вполне известна: это силы, действующие
на сторонние и связанные заряды в
электрическом поле. Примеры таких сил:
заряженный металлический шар (Кулоновские
силы расталкивают заряды и пытаются
растянуть поверхность) и диэлектрик в
конденсаторе (происходит втягивание
диэлектрика внутрь конденсатора).Сила,
действующая на какой-либо заряд,
определяется, очевидно, напряженностью
того поля, в которое помещен этот заряд
(а не того поля, которое возбуждается
им самим):![]() Сила,
действующая на непрерывно распределенный
заряд, записыв. аналогично:
Сила,
действующая на непрерывно распределенный
заряд, записыв. аналогично:![]() и тогда объемная плотность сил
равна:
и тогда объемная плотность сил
равна:![]() Силы,
действующие на поверхностные заряды.Если
имеется поверхность, заряженная
плотностью заряда
Силы,
действующие на поверхностные заряды.Если
имеется поверхность, заряженная
плотностью заряда
![]() , то электрическое поле известно по обе
стороны, причем
, то электрическое поле известно по обе
стороны, причем
![]() ,
а на самой поверхности электрическое
поле не определено. Как искать силу,
действующую на единицу поверхности?
,
а на самой поверхности электрическое
поле не определено. Как искать силу,
действующую на единицу поверхности?
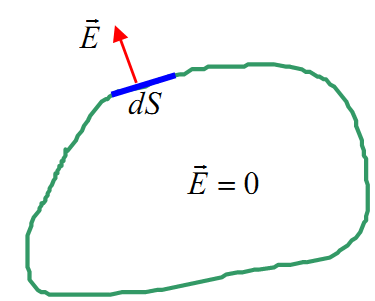
Рассмотрим уединенный проводник с поверхностной плотностью заряда Взаимодействие зарядов растягивает поверхность проводника. Рассмотрим элемент поверхности dS:
1) поле с внешней стороны равно:
![]() ,
где n-единичный вектор нормали
,
где n-единичный вектор нормали
2) поле внутри Е = 0. Поле внутри и снаружи складывается из поля, создаваемого самим
кусочком dS - Е', и из поля всех остальных зарядов - Е''. Поле Е' одинаково по величине по обе
стороны от площадки
dS, но противоположное по направлению.
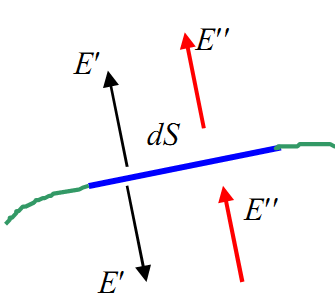
Поле Е'' одинаково
чуть выше и чуть ниже площадки dS в силу
непрерывности. Тогда с внешней стороны
dS имеем:![]()
С внутренней
стороны проводника имеем:![]()
из этих соотношений получаем поле, в котором находится элемент заряженной поверхности dS:
![]() Тогда
сила, испытываемая зарядом dS на элементе
поверхности, определяется полем Е'' и
равна:
Тогда
сила, испытываемая зарядом dS на элементе
поверхности, определяется полем Е'' и
равна:![]()
Пондеромоторная сила, действующая на единицу поверхности,
поверхностная
плотность пондеромоторных сил:
![]() Или
в векторной форме имеем для поверхностной
плотности сил:
Или
в векторной форме имеем для поверхностной
плотности сил:![]()
Фактически, если рассматривать модуль этого выражения, это есть давление, испытываемое поверхностью под влиянием кулоновских сил отталкивания.
Определение
пондеромоторных сил из энергии.Один
из общих способов определения сил через
производную от энергии системы:![]()
В качестве примера рассмотрим силы, действующие на пластины плоского конденсатора .
Энергия
пл.кон.равна:![]() В
этом случае оператор градиента в
сводится к производной энергии по
расстоянию между пластинами d: и тогда
получаем силу, действующую на пластины
конденсатора
В
этом случае оператор градиента в
сводится к производной энергии по
расстоянию между пластинами d: и тогда
получаем силу, действующую на пластины
конденсатора![]()
Проявлением пондеромоторных сил объясняются механические напряжения в диэлектрических слоях, подъем или втягивание жидкого диэлектрика в конденсатор и т.д.
Закон Био-Савара-Лапласа
Осн. задача магнитостатики состоит в умении рассчит. хар-ки полей. Закон Б-С-Л с использованием принципа суперпозиции даёт простейший метод расчёта полей.
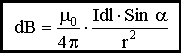
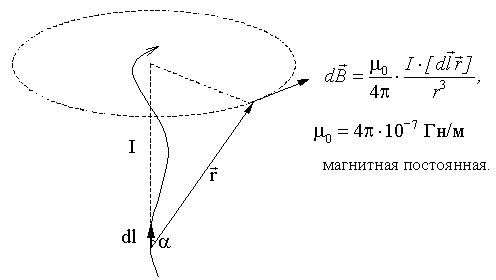
Индукция магн. поля, созданная элементом проводника dl с током I в точке A на расстоянии r от dlпропорц. силе тока, dl, синусу угла между r и dl и обр. пропорцион. квадрату расстояния r. Значение з-на Б-С-Л заключается в том, что зная dH и dB от dl можно вычислить H и B проводника конеч. размеров разл. форм.
Применение з-на Б-С-Л .Поле прямого отрезка конечной длины с током.
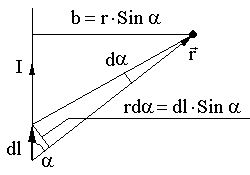
Независимо
от положения dl
на проводнике все dB
направлены в одну строну от нас.значитB=![]() без векторов
без векторов
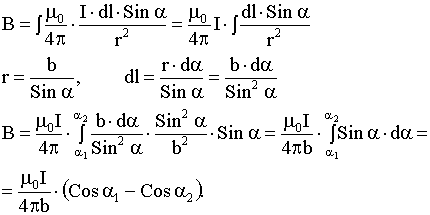
Для бесконечного проводника α1 =0, α2 =π, Сosα1 -Сosα2 =2
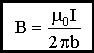
магнитныеединицы СИ и СГС
В системе СГС магнитная индукция поля В измеряется в гауссах (Гс), в системе СИ — в теслах (Тл) 1 Тл = 104 Гс
Напряжённость
магни́тногопо́ля —
это векторная физ.в,
равная разности вектора магнитной
индукции B и вектора
намагниченности J.В
СИ:![]() ,
где μ0 - магнитная
постоянная
,
где μ0 - магнитная
постоянная
В СГС: ![]() В
системе СГС напряжённость
в Эрстедах (Э),
в системе СИ —
в амперах на метр (А/м).
1 Э = 1000/(4π) А/м = 79,5775 А/м.
В
системе СГС напряжённость
в Эрстедах (Э),
в системе СИ —
в амперах на метр (А/м).
1 Э = 1000/(4π) А/м = 79,5775 А/м.
Магни́тныйпото́к — поток Ф как интеграл вектора магнитной индукции В через конечную поверхность S. В системе СИ единицей магнитного потока является Вебер (Вб, размерность — В·с = кг·м²·с−2·А−1), в системе СГС — максвелл (Мкс); 1 Вб = 108 Мкс.
