Лекция 9 ЦЕНТР ТЯЖЕСТИ

9.1 Общие формулы для координат центра тяжести

Рассмотрим тело, находящееся возле поверхности Земли. На каждую частицу этого тела действует сила притяжения, направленная по вертикали вниз и равная весу этой частицы (рис.9.1). Обозначим эту систему сил через р₁, р₂, …, р_n. Строго говоря, данная система сил представляет собой систему сходящихся сил, так как они пересекаются в одной точке – центре земли.

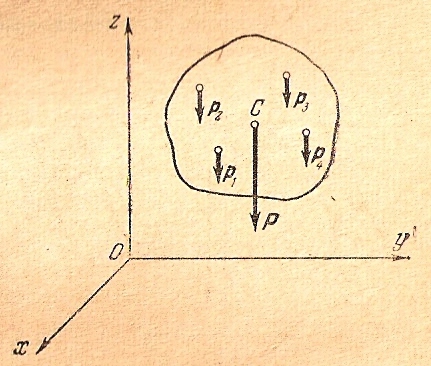
Рис.9.1

Но так как расстояние до центра земли очень велико по сравнению с размерами тела, то с большой степенью точности можно считать, что все эти силы параллельны. Центр С этой системы параллельных сил называется центром тяжести данного тела, а равнодействующая этих сил , проходящая через точку С, представляет собой вес этого тела.

Найдем положение центра тяжести данного тела. Отнесем это тело к прямоугольной системе координат Охуz. Чтобы определить положение центра тяжести С, нужно найти его координаты, которые обозначим через х_С, у_С и z_С. Так как центр тяжести есть центр параллельных сил, представляющих веса элементарных частиц этого тела, то координаты центра тяжести системы параллельных сил будут равны:

, , , где х, у и z обозначают координаты точек приложения р_i.

Обозначим вес единицы объема данного тела через γ, а объемы элементарных частиц через . Если данное тело однородно, то величина γ будет для всех частиц одинакова, т.е. 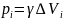. Подставляя эти значения в предыдущие формулы, получим:

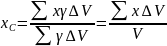, где – объем тела.

Аналогично получим и для двух других координат:

,

Чтобы получить точные формулы для координат центра тяжести однородного тела, нужно перейти к пределу предполагая, что число составляющих тело частиц бесконечно, а объем каждой частицы стермится к нулю. Поэтому окончательно будем иметь:

, ,

Вычисление пределов сумм, входящих в полученные формулы производится методами интегрального исчисления.

1. Случай однородного твердого тела

2. Однородная плоская фигура (рис.19.2)

Рис.9.2

3. Однородная линия (рис.9.3)

Рис.9.3

Тройной интеграл вычисляется следующим образом:

Устанавливаем пределы интегрирования по оси z в виде уравнений поверхности и и интегрируем по направлению оси z:

, при интегрировании х и у рассматриваются как постоянные. Далее тройной интеграл может быть представлен в виде двойного, который приводится к повторному. Интегрируя сначала по у, а затем по х получим

9.2. Положение центра тяжести симметричного тела

Лемма. Если точки приложения всех данных параллельных сил лежат в одной и той же плоскости или на одной и той же прямой, то центр этой системы параллельных сил лежит соответственно в той же плоскости или на той же прямой.

Доказательство: примем плоскость, в которой лежат точки приложения всех данных параллельных сил, за координатную плоскость Оху. Тогда

, но по заданным условиям , следовательно, , т.е. центр системы параллельных сил лежит в плоскости Оху.

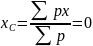Аналогично, примем прямую, на которой лежат точки приложения всех данных параллельных сил, за координатную ось z. Тогда для всех этих точек будем иметь: , следовательно, и

Т.е. центр данной системы параллельных сил лежит на оси z.

Теорема. Если однородное тело имеет плоскость, или ось, или центр симметрии, то центр тяжести такого тела лежит соответственно в этой плоскости, на этой оси или в этом центре симметрии.

Доказательство. Пусть данное тело имеет плоскость симметрии. Тогда мы можем разбить тело на пары одинаковых элементарных частиц равного веса, симметрично расположенных относительно этой плоскости: А₁ и А'₁, А₂ и А'₂ и т.д. (рис.9.4)

Рис.9.4.

Отрезки А₁ А'₁, А₂ А'₂ и т.д. перпендикулярны к плоскости симметрии и в точках пересечения с ней делятся пополам, так что А₁М₁= А'₁М₁, А₂М₂= А'₂М₂, и т.д. Обозначим веса частиц через р₁, р'₁, и т.д. Так как веса симметричных частиц равны, то р₁=р'₁ и т.д. Сложив две равные параллельные силы р₁ и р'₁, приложенные в точках А₁ и А'₁, получим равнодействующую 2р₁, приложенную в точке М₁. Поступив так с весами каждой пары симметричных частиц, получим систему параллельных сил 2р₁, и т.д., точки приложения которых лежат в плоскости симметрии, а следовательно, на основании предыдущей леммы в этой же плоскости лежит и центр тяжести данного тела.

Аналогично доказывается эта теорема и для случаев, когда тело имеет ось или центр симметрии. Эта теорема имеет частые применения. Например, из нее непосредственно следует, что центр тяжести однородной пластинки, имеющей форму параллелограмма, лежит в точке пресечения его диагоналей, центр тяжести однородной эллиптической пластинки лежит в ее геометрическом центре, центр тяжести однородного тела вращения лежит на оси вращения, так как эта ось является для такого тела осью симметрии.