7.5. Векторное и скалярное произведение двух векторов

Пусть имеем два вектора а и в. Перенесем начала этих векторов в точку О. Угол, между этими векторами обозначим через α (рис.7.8)

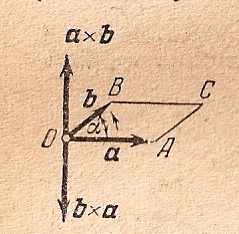
Рис.7.8.

Векторным произведением векторов а и в называется новый вектор, который определяется следующим образом:

1. Модуль этого вектора равен площади параллелограмма построенного на векторах а и в, т.е параллелограмма ОАВС. Так как площадь параллелограмма равна , то модуль векторного произведения двух векторов равен произведению модулей этих векторов, умноженному на синус угла между ними.

2. Этот вектор направлен по перпендикуляру к плоскости параллелограмма ОАВС в ту сторону, чтобы, смотря с конца этого вектора на параллелограмм ОАВС, мы видели поворот первого сомножителя (вектора а) на угол, меньший 180, до совмещения его со вторым сомножителем (вектором в) происходящим в направлении, обратном движению часовой стрелки

Обозначать векторное произведение векторов следующим образом:

Рис.7.9.

Свойства векторного произведения векторов:

1.При изменении порядка сомножителей, векторное произведение меняет свой знак. Модуль этого произведения остается тем же, а направление меняется в противоположную сторону, так как направление поворота вектора b на угол α противоположно направлению вращения на тот же угол вектора а.

2.Равенство нулю векторного произведения двух векторов является условием параллельности этих векторов.

Если векторы а и b параллельны, то угол α между ними равен 0 или 180, . Поэтому векторное произведение этих векторов равно 0.

Если , то . В частности .

3. Если векторы а и b перпендикулярны, то три вектора а, b и будут ориентированы по отношению друг к другу так же, как оси х, у и z прямоугольной, правой системой координат. Так как в этом случае α=90 и , то модуль произведения равен произведению модулей векторов а и b, т.е. если , то

4. Для координатных вектороврис.7.9. исходя из свойства 3 можно получить следующие формулы:

5. Из определения векторного произведения следует, что для умножения этого произведения на скалярный множитель λ достаточно умножить на этот скалярный множитель один из сомножителей векторного произведения:

6. Векторное произведение суммы двух векторов на третий вектор равно сумме векторных произведений каждого слагаемого на вектор множитель: - свойство распределительности.

7. При векторном умножении одного векторного многочлена на другой нужно каждый член множимого векторно умножить на каждый член множителя и результаты сложить.

Выведем формулу разложения векторного произведения по координатным осям

и , следовательно,

Умножая векторно по правилу 4 и 7, получим:

или в форме определителя:

Скалярные коэффициенты при единичных векторах являются проекциями вектора на координатные оси:

Так как по трем проекциям вектора можно найти его модуль и направление (направляющие косинусы), то по этим формулам, когда известны проекции векторов а и b, можно аналитически определить модуль и направление векторного произведения.

Скалярным произведением двух векторов называется скалярная величина, равная произведению модулей этих векторов, умноженному на косинус угла между ними.

Скалярное произведение двух векторов будем обозначать знаком умножения в виде точки: . Если угол между векторами а и b обозначить как α, то по определению: : . В зависимости от знака произведение может быть положительным или отрицательным.

Свойства скалярного произведения:

1. Скалярное произведение двух векторов обладает свойством переместительности:

2. Если векторы а и b параллельны и направлены в одну сторону, то α=0 и , следовательно, : . Если направлены в противоположные стороны, то и

В частности, скалярное произведение двух равных векторов равно квадрату модуля одного из сомножителей:

3. Если векторы а и b перпендикулярны, то и :

Равенство нулю скалярного произведения двух векторов выражает условие перпендикулярности этих векторов.

4. Если перемножать скалярно координатные векторы, то получим:

5. Для умножения скалярного произведения на некоторый скалярный множитель достаточно умножить на этот множитель один из сомножителей скалярного произведения:

6. Скалярное произведение суммы двух векторов на третий вектор равно сумме скалярных произведений каждого слагаемого на вектор множитель (свойство распределительности):

При скалярном умножении одного векторного многочлена на другой нужно каждый член множимого скалярно умножить на каждый член множителя и результаты сложить

7. Скалярное произведение одного вектора на единичный вектор другого равно проекции первого вектора на направление второго.

7. Скалярное произведение двух векторов a и b можно выразить через проекции этих векторов на координатные оси:

и

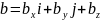
Раскрывая скобки, на основании правила 6 получим:

Эта формула позволяет найти скалярное произведение двух векторов по их проекциям на координатные оси.

8