Лекция 2 Сходящиеся силы

2.1. Сложение сил, приложенных в одной точке

Система сил, линии действия которых, пересекаются в одной точке, называется системой сходящихся сил.

Так как точки приложения сходящихся сил можно перенести по линиям их действия в точку пересечения этих линий, то систему сходящихся сил всегда можно заменить системой сил, приложенных в одной точке. Сложить несколько сил означает, что надо заменить эти силы одной, им эквивалентной, т.е. найти их равнодействующую. Задача о сложении двух сил, приложенных к твердому телу в одной точке, решается, согласно аксиоме 3, на основании правила параллелограмма: равнодействующая двух сил, составляющих между собой некоторый угол, равна по модулю и направлению диагонали параллелограмма, построенного на этих силах (рис.2.1.). Обозначим угол между данными силами F₁ и F₂ через α, а углы, которые равнодействующая R образует с этими силами, обозначим соответственно через φ₁ и φ₂.

Рис.2.1.

Из треугольника ADC находим:

, откуда (2.1)

По теореме синусов: , откуда и (2.2)

Формулы (2.1) и (2.2) позволяют определить модуль и направление равнодействующей двух данных сил F₁ и F₂, образующих между собой угол α.

При нахождении равнодействующей двух сил не обязательно строить весь параллелограмм. Достаточно из конца вектора первой силы F₁ (рис.2.2) провести вектор второй силы F₂ и вектор, соединяющий начальную и конечную точки полученной ломаной линии, изобразит по модулю и направлению равнодействующую R двух данных сил F₁ и F₂ (правило треугольника).

Рис.2.2.

Сложение трех сил, не лежащих в одной плоскости

Применяя последовательно правило параллелограмма, можно найти равнодействующую множества сходящихся сил. Найдем равнодействующую для трех сил F₁, F₂ и F₃, не лежащих в одной плоскости и приложенных в одной точке (рис.2.3). Сложив по правилу параллелограмма силы F₁ и F₂, получим их равнодействующую R₁; сложив по тому же правилу силы R₁ и F₃, найдем равнодействующую R трех данных сил F₁, F₂ и F₃.

Рис.2.3.

Очевидно, что равнодействующая трех сил, приложенных в одной точке и не лежащих в одной плоскости, равна по модулю и направлению диагонали параллелепипеда, построенного на этих трех силах (правило параллелепипеда).

Сложение нескольких сил. Пусть нужно сложить несколько сил (например, силы ), приложенных в точке А (рис.2.4). Сложим сначала две первые силы F₁ и F₂, для этого из конца вектора первой силы F₁ проводим , равный вектору второй силы F₂; вектор изобразит равнодействующую сил F₁ и F₂. Сложим теперь силы и F₃. Для этого проведем из точки С вектор , равный вектору , и соединим точки А и D. Вектор представляет собой равнодействующую сил и или (что то же) равнодействующую сил . Складывая силы и , из точки D проведем вектор , равный вектору , и соединим токи А и Е; вектор изображает искомую равнодействующую R четырех сил .

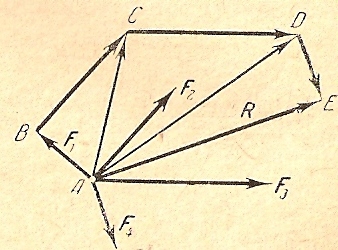
Рис.2.4.

Правило силового многоугольника:

Равнодействующая нескольких сходящихся сил выражается по модулю и направлению вектором, соединяющих начальную и конечную точки ломаной линии, стороны которой представляют собой векторы, равные векторам, изображающим данные силы (вектором, замыкающим эту ломаную линию); линия действия этой равнодействующей проходит через точку пересечения линий действия данных сил. Ломаная линия называется силовым многоугольником.

Сложение сил по правилу силового многоугольника является геометрическим сложением векторов и совпадает с общим правилом сложения векторов:

Равнодействующая системы сходящихся сил равна по модулю и направлению их геометрической сумме и изображается вектором, равным сумме векторов, изображающих данные силы. Равнодействующая двух сил, равных по модулю и направленных по одной прямой в противоположные стороны равна нулю.