2. Модель вход-состояние-выход

2.1 Понятие состояния и уравнение состояния

Рассмотрим электрическую цепь известной структуры, содер­жащую один вход и один выход.

Входным сигналом цепи служит функция времени v(t), а вы­ходным— функция времени у(t). Имея полную информацию о цепи, для определения выхода y(t) на интервале времени (t₀, t) достаточно знать входной сигнал v(t) на всем данном временном интервале. Одна­ко, если вход известен лишь а интервале времени (to, t), для определения выхода у(t) на указанном интервале необходимо знать токи на индуктивности и напряжения на конденсаторе в некоторый момент времени t*

Эти токи и напряжения образуют «состояние» цепи в момент t*.. В этом смысле состояние цепи связывается с ее памятью. В слу­чае чисто активной цепи (с нулевой памятью) для определения текущего значения выхода требуется только знание текущего значения входа.

В качестве другого примера состояния системы рассмотрим решение линейного дифференциального уравнения с постоян­ными коэффициентами при t₀ t. Так как общее решение полу­чается зависящим от произвольных постоянных, то эти постоян­ные можно определить из условия удовлетворения системы граничным условиям в момент времени t₀. Никакой иной инфор­мации не требуется. Граничные условия могут трактоваться как состояние системы в момент t₀. Эвристически состояние системы отделяет будущее от прошлого, так что состояние содержит всю информацию о прошлом системы, необходимую для опре­деления реакции на произвольный входной сигнал.

Понятие состояния является основным понятием и, следо­вательно, не может быть определено более полно, чем, напри­мер, слово «множество» в математике. Наибольшее, что можно сделать в этом плане, это сформулировать свойства, какими должна обладать система, поведение которой отвечает понятию состоянияРассматриваемые здесь системы относятся к детер­минированным. Детерминированная система определяется сле­дующими образом:

1) Существует класс функций времени v(t), называемых до­пустимыми функциями входа

2) для каждого мо­мента времени t опреде­ляется множество Х_t эле­менты которого х(t) яв­ляются возможными со­стояниями;

3) каждой паре v(t), x(t) отвечает по крайне мере хотя бы одна функция времени, называемая функцией выхода, и для всякого t*>t в X содержится единственный элемент x(t*)

Условия, предъявляемы к множеству X_t можно записать в виде двух урав­нений, называемых уравнениями состояния:

(2.1.1)

(2.1.2)

где как g, так и f являются однозначными функциями. Из урав­нения (2.1.1) следует, что выходной сигнал у на Интервале (to, t) является однозначной функцией входного сигнала v на этом ин­тервале времени и состояния в начале интервала. Состояние в конце интервала, как это следует из уравнения (2.1.2), является однозначной функцией такого же аргумента. Указанные два уравнения задают систему с определенным в ней состоянием.

В качестве составляющих вектора состояния в схеме моде­лирования большей частью используются выходы интеграторов.

Вектор состояния определяется в n-мерном пространстве состояний с координатами х_и х₂, ..., х„. Движение конца век­тора состояния в пространстве состояний называется траекто­рией вектора состояния.

Для системы, описываемой системой обыкновенных линейных

дифференциальных уравнений, уравнения состояния записываются как:

x(t) = A(t)x(t)+B(t)v(t), (2.1.3)

y(t) = C(t)x(t) + D(t)v(t)

где, A(t), B(t), C(t) и D(t) являются в общем случае матрицами с изменяющимися во времени коэффициентами. x, v и y – векторы размерности n, m и p соответственно.

В общем случае блок-схема, соответствующая (2.1.3) изображена на рисунке ниже

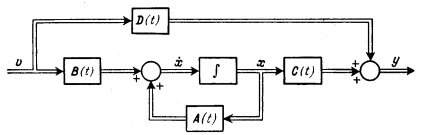
Если коэффициенты системы не меняются во времени, то в дальнейшем будем их обозначать просто A, B, C и D.