3. Решение дифференциальных уравнений

Рассмотрим схему решения линейного дифференциального уравнения первого порядка, за­писанного в виде:

. (1.4.1)

Для удобства коэффициент при dy/dt полагаем равным единице. Коэффициент а в общем случае может зависеть от времени Данное уравнение решается пу­тем введения интегрирующего множителя . Умножим на него обе части уравнения (1.4.1):

Левая часть этого уравнения является производной по времени от , так что

, c = const. (1.4.2)

Хотя интегрирование правой части уравнения (1.4.2) порой представляет определенные трудности, изложенный метод предлагает строгую процедуру решения дифференциального уравнения вне зависимости от вида его коэффициента a(t). Ре­зультат содержит обе составляющих решения.

При вычислении ∫a(t)dt нет необхо­димости записывать постоянную интегрирования.

Следует учитывать, что решение дифференциальных уравнений более высокого порядка в общем случае, когда коэффициенты зависят от времени, является довольно сложной задачей. Однако, как правило, если коэффициенты меняются медленно, то можно считать их постоянными, поэтому далее будем рассматривать схему решения уравнений с постоянными коэффициентами.

Линейные стационарные системы описываются линейными дифференци­альными уравнениями с постоянными коэффициентами. Однородное и неод­нородное уравнения n-го порядка задаются соответственно уравнениями (1.3.1) и (1.3.2), где а_i постоянные коэффициенты.

Решение однородных ДУ с постоянными коэффициентами

Рассмотрим уравнение n- го порядка

(a_npⁿ + a_n-1p^n-1 +…+ a₁p + a₀)y = 0. (1.4.3)

Предположим, что решение имеет вид y=e^rt, где r- подлежащая определению постоянная величина. Подставив предполагаемое решение в уравнение (1.4.3) получим

(a_nrⁿ + a_n-1r^n-1 +…+ a₁r + a₀)e^rt = 0. (1.4.4)

Так как это уравнение удовлетворяется при всех значениях t ( ), то

a_nrⁿ + a_n-1r^n-1 +…+ a₁r + a₀ = 0. (1.4.5)

Уравнение (1.4.5) называют вспомогательным или характеристическим. Его можно записать не­посредственно из уравнения (1.4.3). В левой части (1.4.5) стоит полином n-го порядка, так что оно содержит n корней. Обозначим корни через r1; r2, ...,г_n. Тогда соответствующие решения уравнения (1.4.3) равен

y₁ = e^r1t, y₂ = e^r2t,…, y_n = e^rnt.

Если эти n ре­ше­ний ли­нейно неза­ви­симы, то об­щее ре­ше­ние одно­род­ного диф­фе­рен­ци­аль­ного урав­нения имеет вид

y_н = K₁e^r1t + K₂e^r2t +…+K_ne^rnt.

Если все корни г_i раз­ные, то из (1.3.3) сле­дует, что опре­дели­тель Врон­ского отли­чен от нуля и, та­ким обра­зом, n от­дель­ных ре­ше­ний неза­ви­симы. Если r₁ = r₂, то не­зави­симы реше­ния y₁ = e^r1t и y₂ = te^r2t. Если, на­при­мер, r₁ имеет крат­ность k, т.е. r₁ = r₂ =...= r_k то общее ре­ше­ние запи­сыва­ется в виде

y_н = K₁e^r1t + K₂te^r1t +…+ K_kt^k-1e^r1t + K_k+1te^r(k+1)t +…+K_ne^rnt

Та­ким обра­зом, для на­хож­дения уⁿ тре­бу­ется только вы­чис­ление кор­ней урав­нения n-го по­рядка. В связи с тем, что неко­торые корни могут быть ком­плексными, ре­ше­ние урав­нения можно за­пи­сать в дру­гой форме.

По­скольку ко­эффи­ци­енты урав­нения (1.3.2) дейст­ви­тель­ные, ком­плексные корни должны быть ком­плексно со­пря­жен­ными. Так, если один из кор­ней равен r₁ = α+iβ, где α и β - дейст­ви­тель­ные вели­чины, то другой из кор­ней дол­жен быть r₂ = α-iβ. Тогда

K₁e^r1t + K₂e^r2t = e^αt(K₁e^iβt + K₂e^-iβt) = e^αt[(K₁ + K₂)cosβt + i(K₁ - K₂)sinβt] =

= e^αt[Acosβt + Bainβt].

В реальной системе а_i — действительные числа, а у_n — действительная функция времени. Поэтому произвольные постоянные А и В должны быть действительными числами, что в свою очередь означает, что К₁, и К₂ должны быть комплексно сопряженными. Учитывая, что два тригонометрических выражения одинаковой частоты можно свести к одному с фазовым углом, возможна также запись

K₁e^r1t + K₂e^r2t = Ke^αtcos(βt + φ).

Решение неоднородных ДУ с постоянными коэффициентами.

Метод неопределенных коэффици­ентов. Рассмотрим уравнение

(a_npⁿ + a_n-1p^n-1 +…+ a₁p + a₀)y = F(t). (1.4.6)

решение которого имеет вид

y = y_н + y_p (1.4.7)

у_n определяется при F(t)=0 из решения соответствующего од­нородного уравнения, как ука­зано раньше. Существуют два стандартных метода нахождения частного решения у_р - ме­тод неопределенных коэффициентов и метод вариации параметров.

Метод неопределенных коэффициентов применяется в том случае, когда вы­нуждающая функция F(t) имеет конечное число линейно независимых производных. F(t) может быть многочленом целой положительной степени t или состоять из комбинации экспоненциальной, синусоидальной или гиперболической функций. При F(t), например, равной In t или , указанный метод неприменим (если не искать ре­шение в виде бесконечного ряда). В силу ограниченности данный метод при проектирование систем практически не используется.

В от­личие от ме­тода неоп­реде­лен­ных ко­эф­фи­циен­тов, метод на­хож­дения у_р по­сред­ством ва­риа­ции пара­мет­ров мо­жет при­ме­няться вне зави­симо­сти от­того, имеет или не имеет вы­нуж­даю­щая функ­ция F(t) ко­неч­ное число неза­виси­мых про­из­вод­ных. В от­личие от пер­вого ме­тода он при­ме­ним также и в том слу­чае, если коэф­фици­енты a_i в урав­нении (1.4.6) зави­сят от вре­мени. Ме­тод ва­риа­ции пара­мет­ров пред­пола­гает на­хож­дение част­ного ре­ше­ния на ос­нове со­став­ляю­щих ре­ше­ния одно­род­ного урав­нения.

(a₁p+a₀)y=F(t) (1.4.8)

Ре­ше­ние, удов­ле­тво­ряю­щее одно­род­ному диф­фе­рен­ци­аль­ному урав­не­нию

(а₁р+а₀)у=0 (1.4.9)

со­дер­жит один член у_н=Ку₁ Ча­стное ре­ше­ние ищем в виде y_p=uy₁, где все три вели­чины явля­ются функ­циями вре­мени. Подставим это выражение в уравнение (1.4.8). Полу­чим

a₁(uy + uy₁) + a₀uy₁ = F(t),

где точки обо­зна­чают про­из­вод­ные по t. После пре­обра­зова­ний имеем

a₁uy₁ + u(a₁y₁ + a₀y₁) = F(t).

В по­след­нем урав­нении мно­жи­тель в скоб­ках равен нулю, так как y₁, удов­летво­ряет урав­нению (1.4.9). Сле­дова­тельно,

Пример: Найти общее решение уравнения

Решение однородного уравнения у_н=Ке^-3t, т.е. y₁=e^-3t. Предполагая y_p=ue^-3t

u=ln t и y_p=e^-3tln t.

Общее решение имеет вид

y=Ke^-3t+e^-3tln t.

Рассмотрим дифференциальное уравнение второго порядка:

(a₂p²+a₁p+a₀)y=F(t) (1.4.10)

Решение удовлетворяющее однородному дифференциальному уравнению:

(a₂p²+a₁p+a₀)y=0 (1.4.11)

состоит из двух слагаемых: y_н=K₁y₁+K₂y₂

Частное решение ищем в виде

у_р= u₁y₁+u₂y₂ (1.4.12)

где u₁ и u₂ являются неизвестными функциями времени. Для нахождения u₁ и u₂ тре­буются два условия. Одно из них состоит в том, что уравнение (1.4.12) должно удовлетво­рять уравнению (1.4.10). Другое условие можно выбрать любым наиболее выгод­ным образом

Выражения для и будут менее громоздкими, если положить

u_ly₁+u₂y₂=0 (1.4.13)

Поэтому уравнение (1.4.13) становится вторым из двух необходимых условий:

Подстановка в уравнение (1.4.10) дает

Так как у₁ и у₂ удовлетворяют уравнению (1.4.11), то

u₁y₁+u₂y₂=F(t)/a₂ (1.4.14)

Чтобы получить в явном виде формулы для u₁ и u₂ необходимо решить совместно уравнения (1.4.13) и (1.4.14). Получим

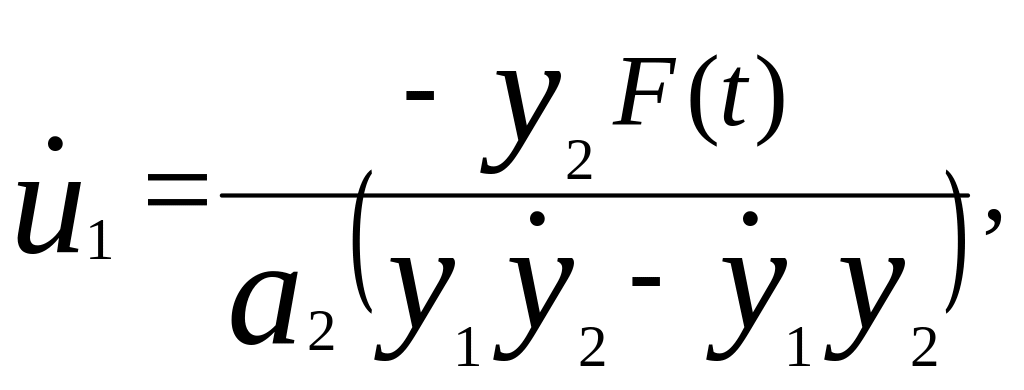
(1.4.15)

Следует отметить, что так как y₁ и у₂ - линейно независимые решения уравнения (1.4.11), то из (1.3.3) сле­дует, что y₁y₂-y₁y₂≠0 Так как знаменатель уравнения (1.4.15) отличен от нуля, u₁ и u₂ всегда существуют.

Рассмотрим дифференциальное уравнение n-го порядка типа

(a_npⁿ+a_n-1p^n-1+...+a₁p+a₀)y=F(t).

Решение однородного уравнения имеет вид

у_н=К₁у₁+К₂у₂+...+К_ny_n.

Частное решение ищем в виде

у_р= u₁y₁+u₂y₂+...+ u_ny_n , (1.4.16)

где u_i являются функциями t. Производные от u_i находим из совместного решения следующих n уравнений:

где точки и верхние индексы обозначают производные по t. Первые n-1 условий выбира­ются произвольно, с целью получения результата в обозримой форме. Последнее уравнение получено при подстановке предполагаемого решения у_р в уравнение (1.4.6) с учетом предыдущих n-1 условий.

Приведенная выше система уравнений решается на основе правила Крамера

i = (1, 2,…, n), (1.4.17)

где

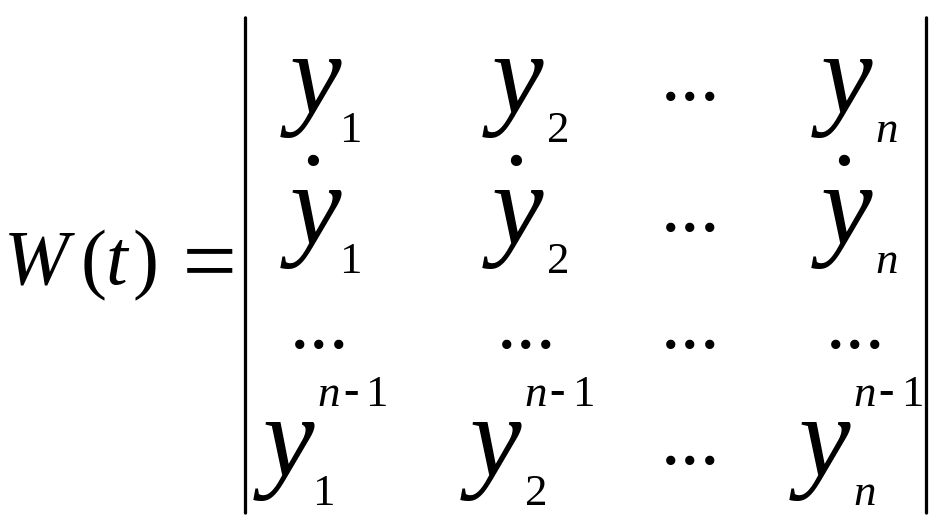, (1.4.18)

a Wni(t) - ni-e алгебраическое дополнение. Из (1.3.3) следует, что W(t)-определи­тель Вронского - отличен от нуля, если y₁, y₂,...,у_n -независимые решения од­нородного дифференциального уравнения.

Хотя метод вариации параметров сложнее, в отличии от метода неопределенных коэффициентов он позволяет получить решение при любой правой части ДУ, и, кроме того, применим к уравнениям с манящимися во времени коэффициентами.

Оди­нако­вые на­чаль­ные усло­вия.

В ряде важ­ных слу­чаев на­чаль­ные усло­вия оди­на­ковы. Для диф­фе­рен­ци­аль­ного урав­нения n-го по­рядка (1.4.6) оди­нако­вые на­чаль­ные усло­вия имеют вид

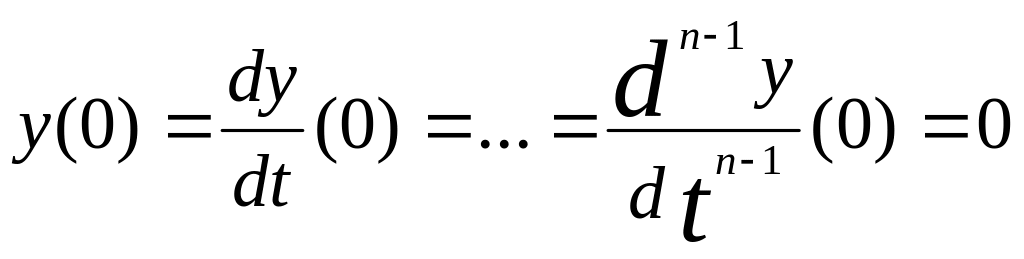(1.4.19)

Ранее ис­поль­зуе­мый для на­хож­дения част­ного ре­ше­ния метод ва­риа­ции пара­мет­ров можно обобщить для полу­чения об­щего ре­ше­ния, удов­ле­тво­ряю­щего ука­зан­ным оди­нако­вым на­чаль­ным усло­виям. При n = 1 урав­нения и y_p=uy₁ объе­диня­ются в

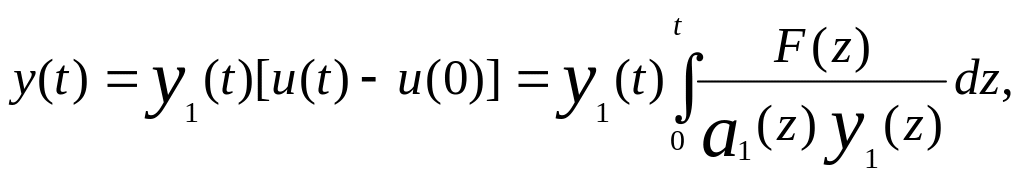(1.4.20)

где у₁(t) - реше­ние одно­род­ного урав­нения, а z - фик­тив­ная пере­мен­ная ин­тег­риро­вания. Верхний пре­дел соот­вет­ст­вует рас­смот­рен­ному ранее част­ному ре­ше­нию, а ниж­ний пре­дел дает по­сто­ян­ную в ре­ше­нии одно­род­ного урав­нения. От­ме­тим, что у(0)=0. При n=2 урав­нения (1.4.12) и (1.4.15) объе­диня­ются в

где y₁(t) и y₂(t) реше­ния одно­род­ного урав­нения, a W(t) — оп­реде­ли­тель Врон­ского,

W(t)=y₁(t)y₂(t)-y₁(t)y₂(t)

При­ве­ден­ные выше заме­чания о пре­делах ин­тег­риро­вания справед­ливы и в этом случае. От­метим, что у(0) = 0 и

Выражение в последней скобке всегда равно нулю, как следует из уравнения (1.4.13), так что соблюдается у(0)=0.

В общем случае дифференциального уравнения n-го порядка при одинаковых начальных условиях из уравнений (1.4.16) и (1.4.17) следует

(1.4.22)

где W(t) и W_ni(t) определяются уравнением (1.4.18). Так как основу рассуждений составляет метод вариации пара­метров, уравнения (1.4.19) и (1.4.22) справедливы как для систем с постоянными, так и с переменными параметрами. Данные уравнения применяются при нахождении импульсной характеристики нестационарной системы.