
- •Методичні вказівки до проведення практичних робіт
- •Практичне заняття № 1 Обчислення визначників План
- •Навчальні завдання
- •Завдання для перевірки знань
- •Практичне заняття № 2 Матриці План
- •Термінологічний словник ключових понять
- •Навчальні завдання
- •Завдання для перевірки знань
- •Практичне заняття № 3 Вектори
- •1. Лінійні операції з векторами.
- •2. Застосування скалярного, векторного і мішаного добутків векторів для розв’язування задач. Термінологічний словник ключових понять
- •Навчальні завдання
- •Завдання для перевірки знань
- •Практичне заняття № 4 Прямі на площині і в просторі План
- •Термінологічний словник ключових понять
- •Навчальні завдання
- •Завдання для перевірки знань
- •Практичне заняття № 5 Криві другого порядку План
- •Завдання для перевірки знань
- •Завдання для перевірки знань
- •Термінологічний словник ключових понять
- •Навчальні завдання
- •Завдання для перевірки знань
- •Обчислення визначених інтегралів
- •Завдання для перевірки знань
- •Практичне заняття № 8-9 Диференціальні рівняння План
- •Термінологічний словник ключових понять
- •Навчальні завдання
- •Завдання для перевірки знань
Термінологічний словник ключових понять
Первісна даної функції — функція, похідна від якої дорівнює даній функції.
Інтегрування функції — знаходження первісних функції.
Невизначений інтеграл від даної функції — загальний вигляд всієї множини первісних даної функції.
Інтегрування розкладом — метод інтегрування, що базується на (8.3).
Інтегрування частинами — метод інтегрування за формулою (8.4).
Метод підстановки — метод інтегрування, що базується на формулах (8.6), (8.7).
«Неінтегровні» інтеграли — існують, але через основні елементарні функції не виражаються.
Навчальні завдання
1.
![]()
![]()
2.
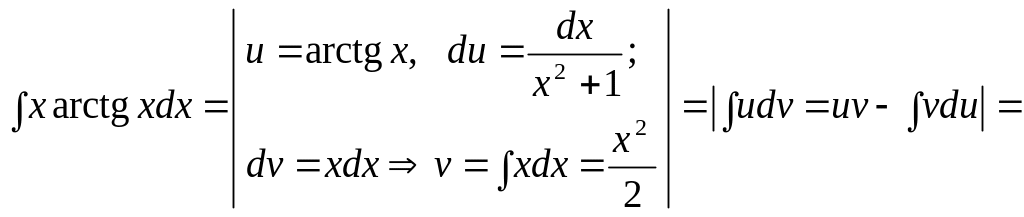
![]()
![]() .
.
3 .
.
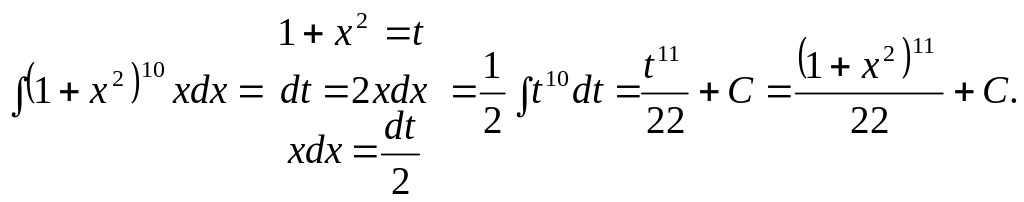
4.
![]()
![]()
5.
![]()
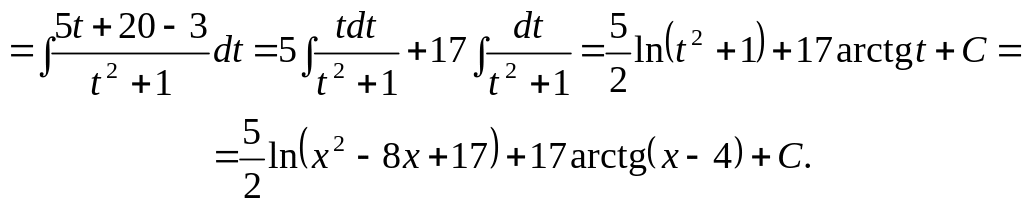
6.
![]()
![]()
![]()
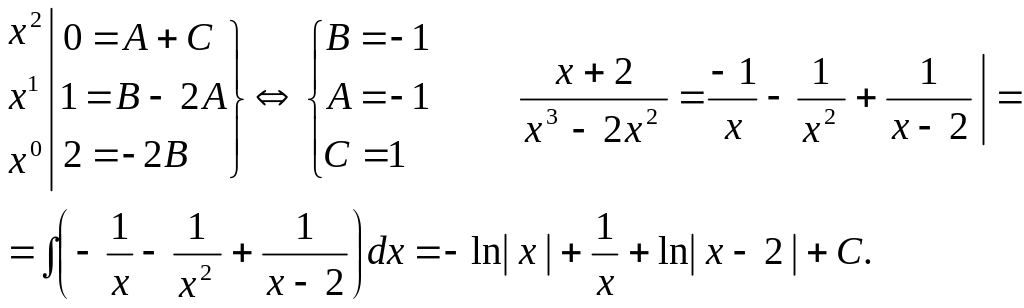
7.
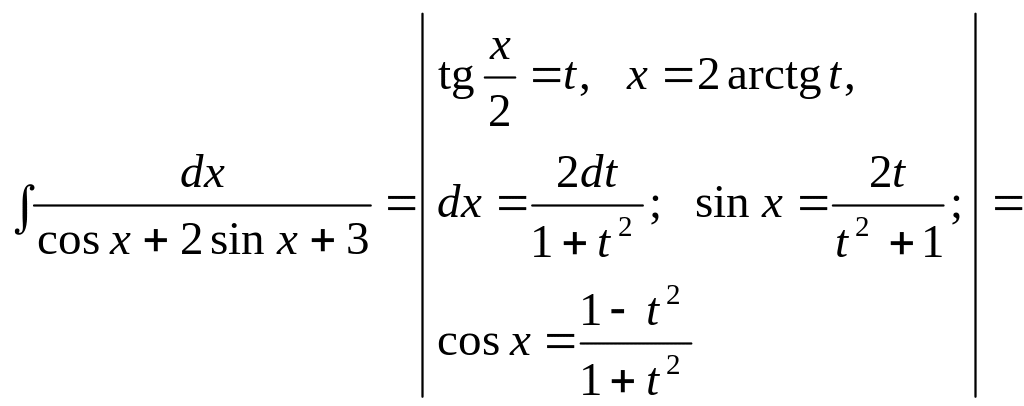
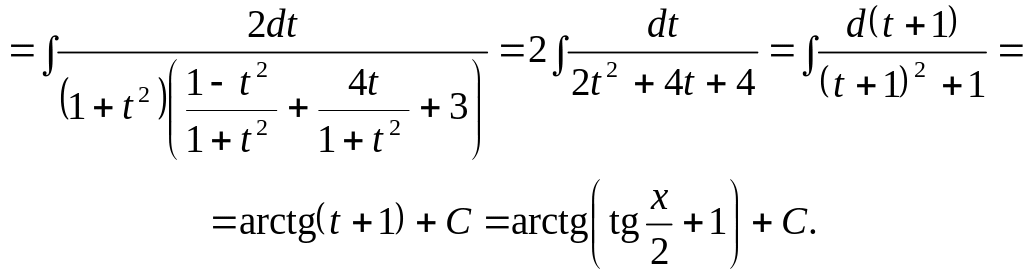
8.
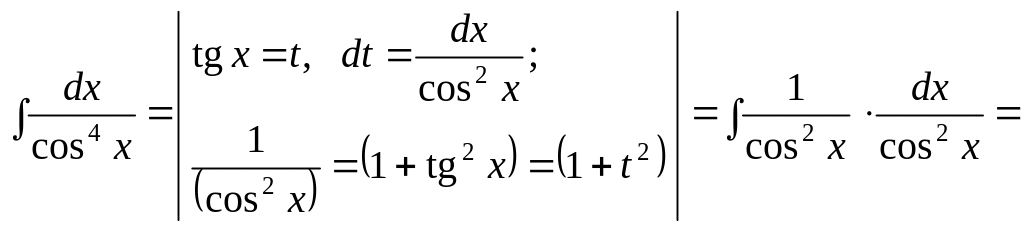
![]()
9.
![]()
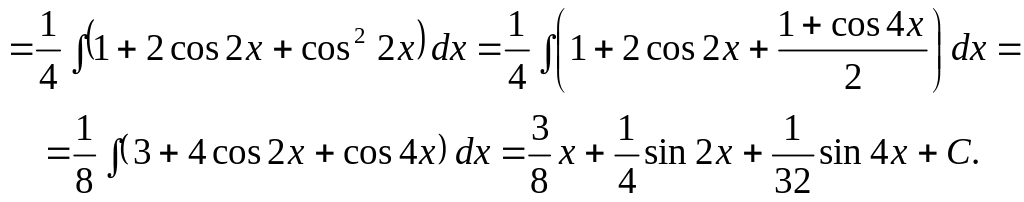
Завдання для перевірки знань
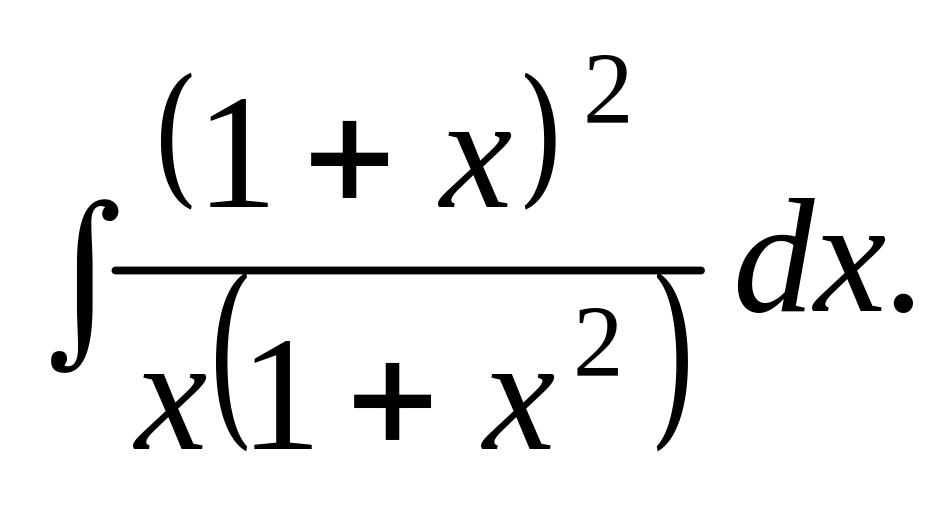 Відповідь.
Відповідь.

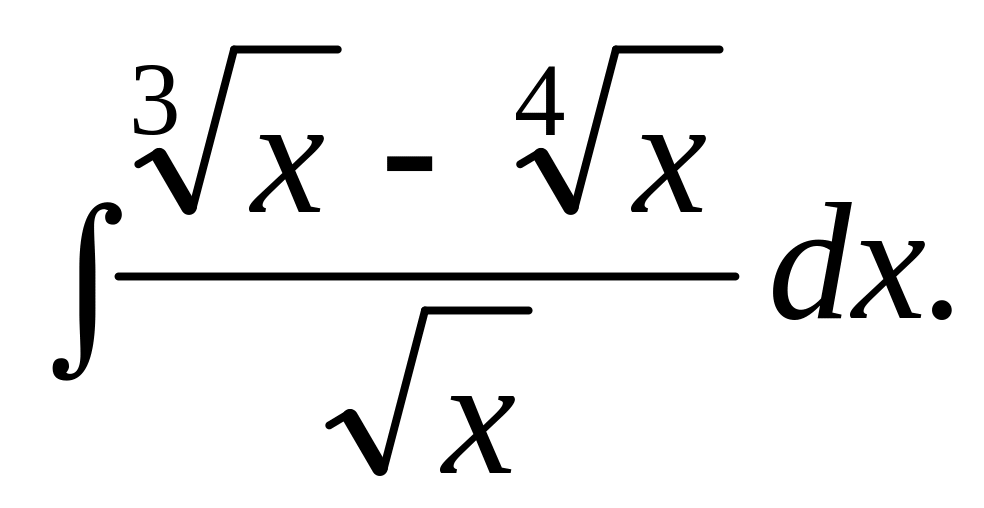 Відповідь.
Відповідь.
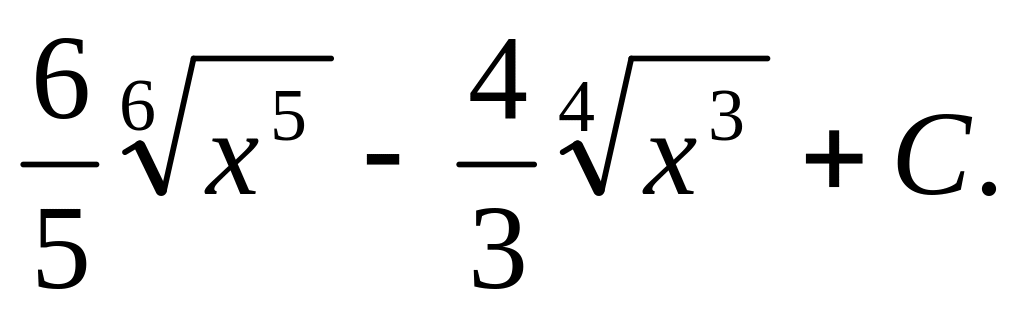
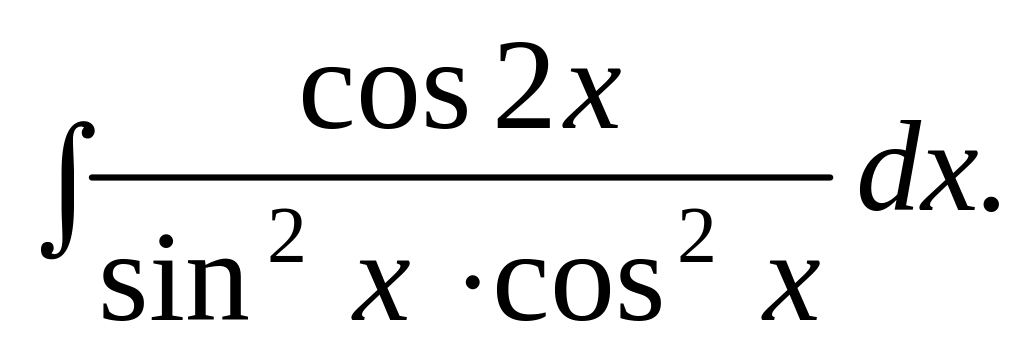 Відповідь.
Відповідь.
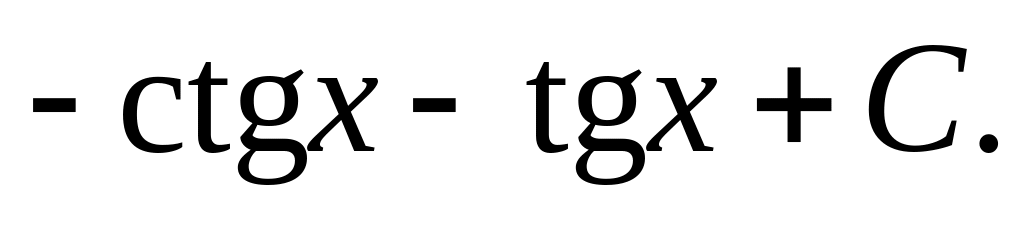
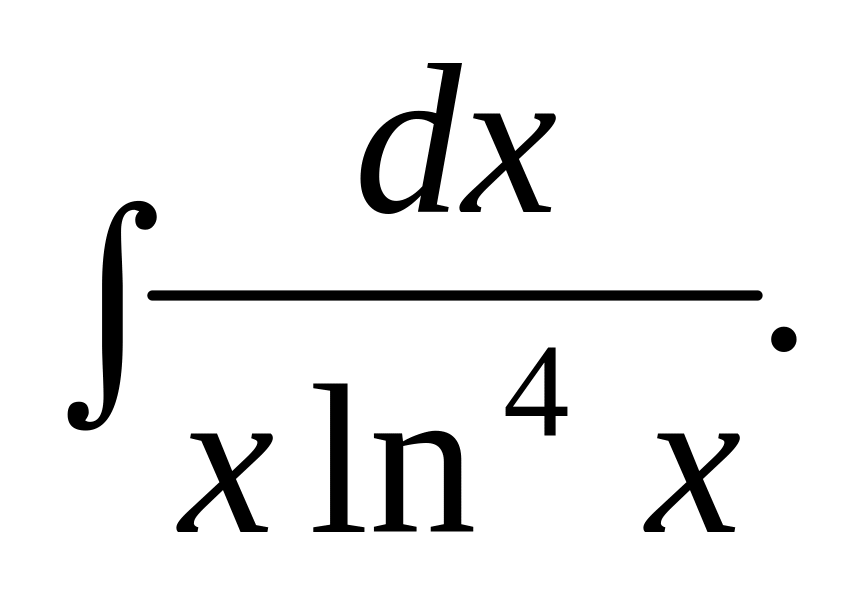 Відповідь.
Відповідь.
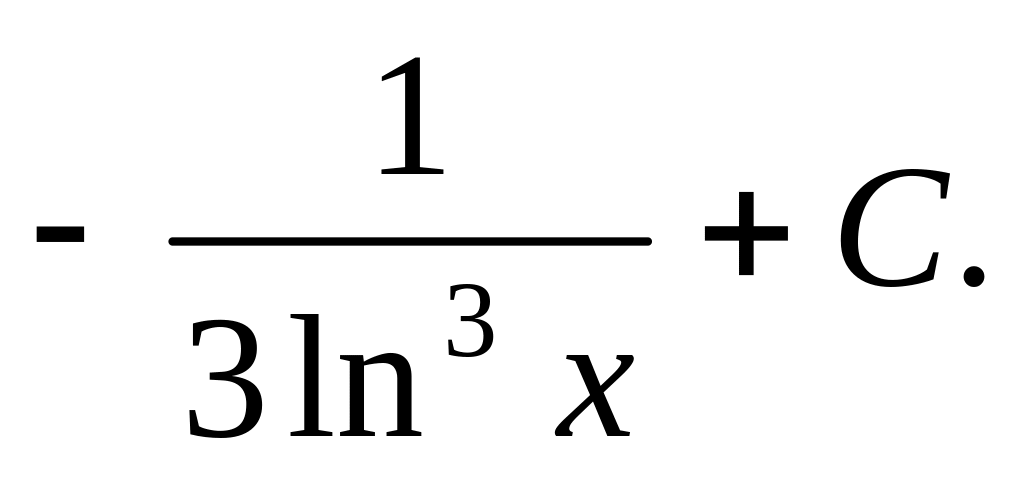
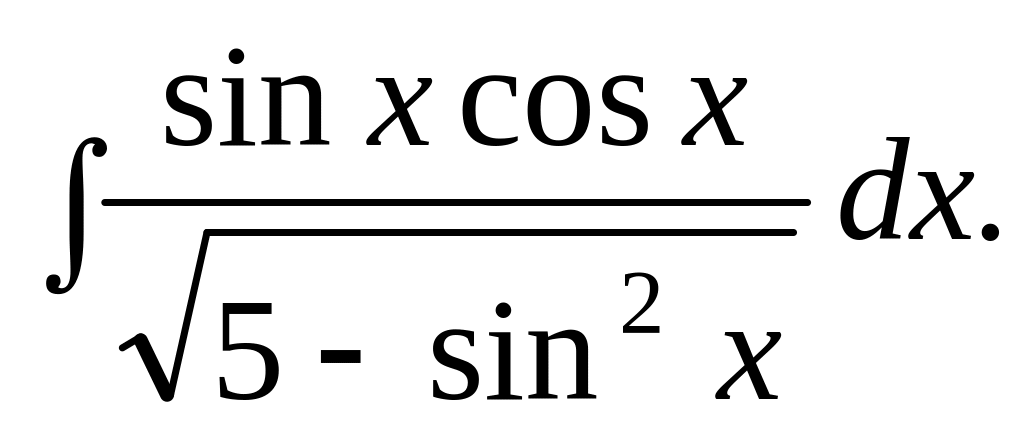 Відповідь.
Відповідь.
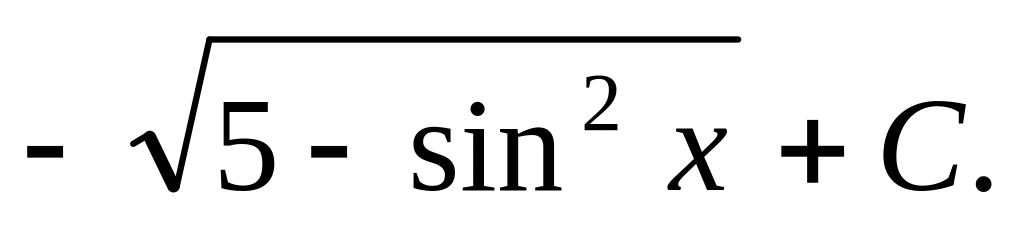
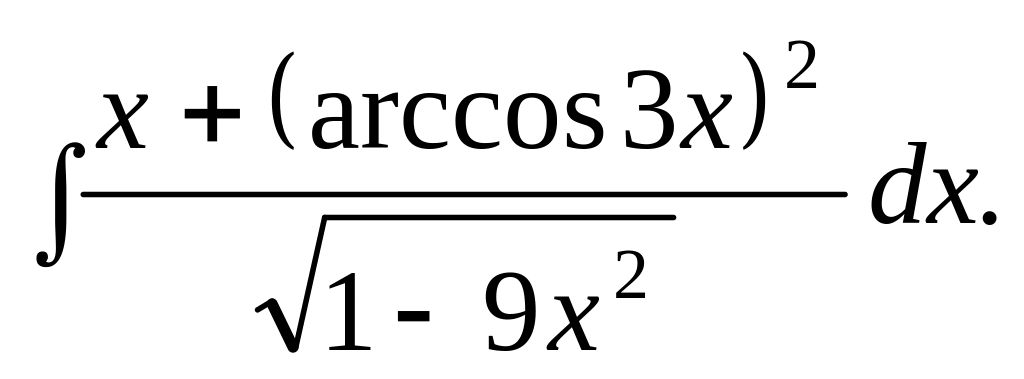 Відповідь.
Відповідь.
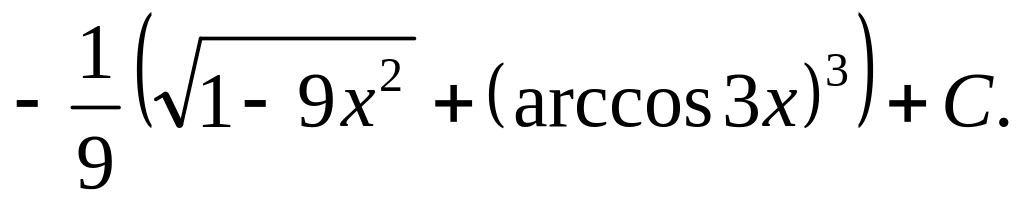
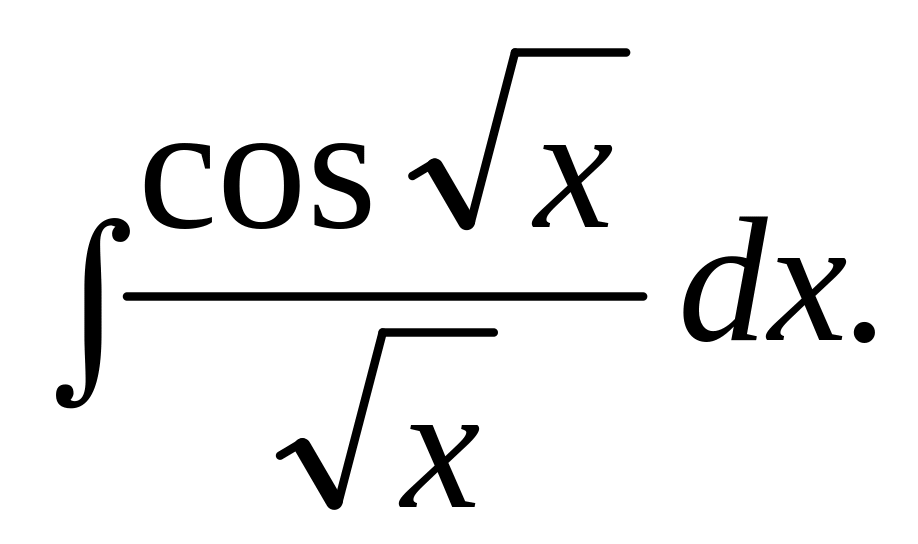 Відповідь.
Відповідь.
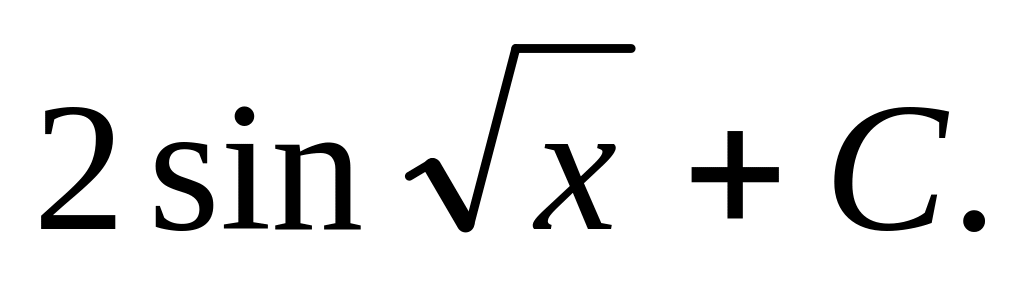
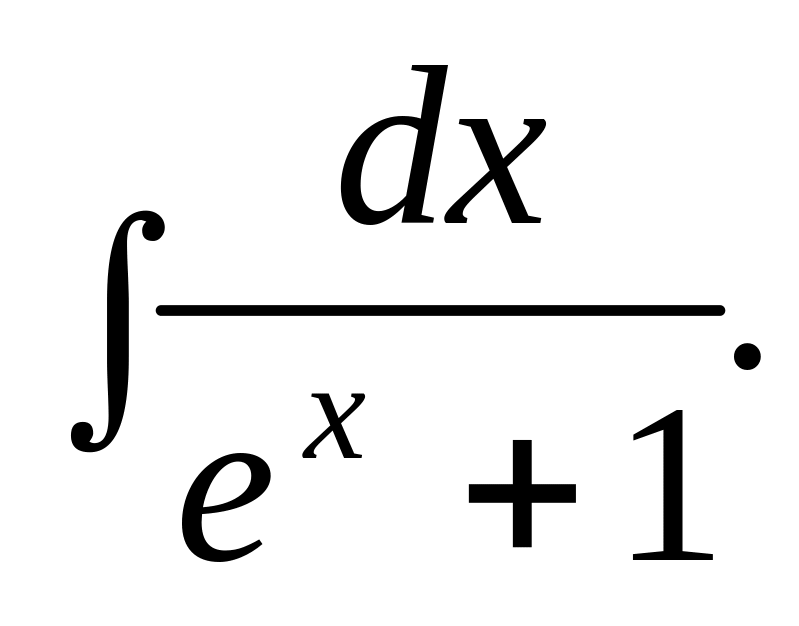 Відповідь.
Відповідь.
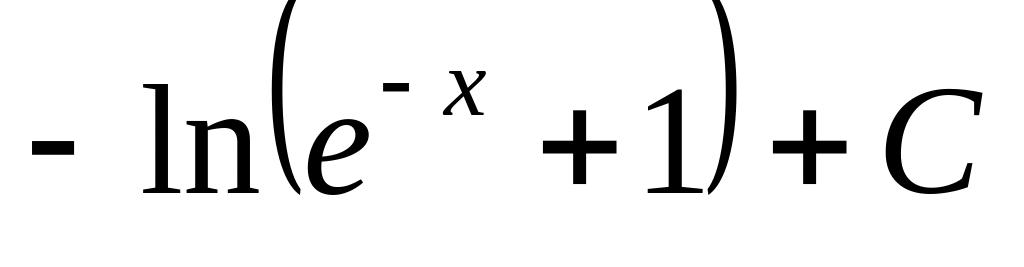 .
.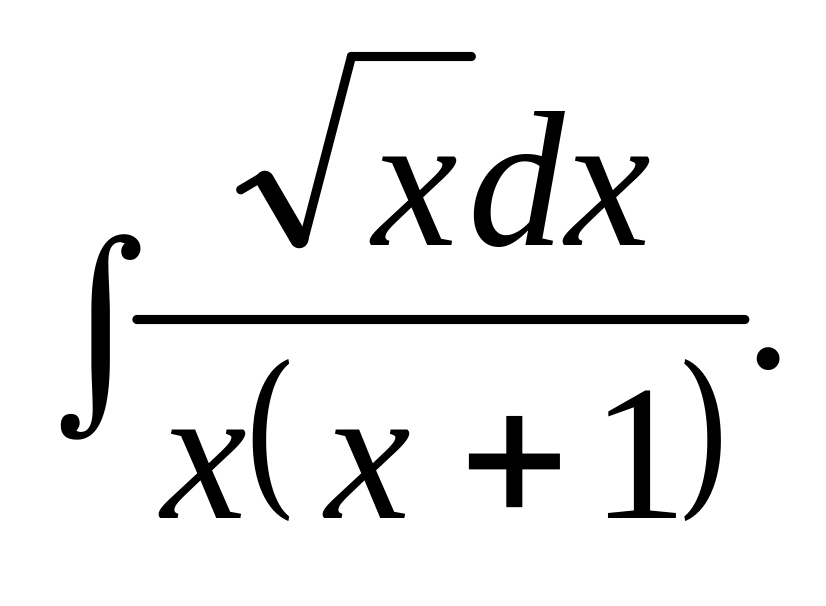 Відповідь.
Відповідь.
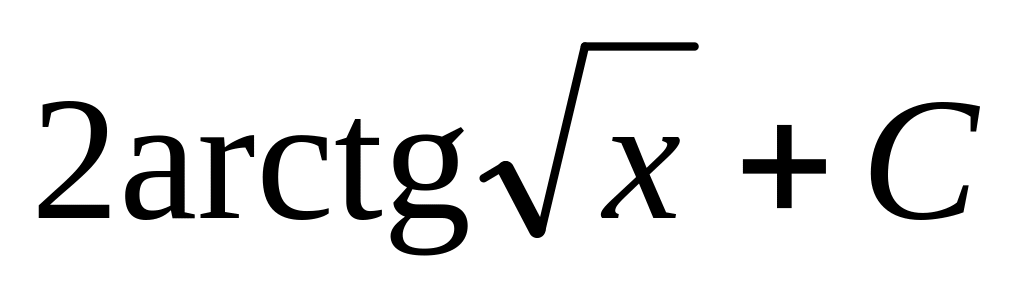 .
.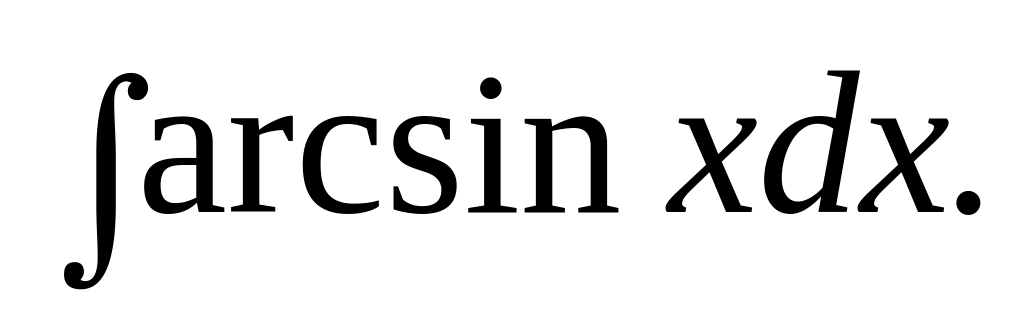 Відповідь.
Відповідь.
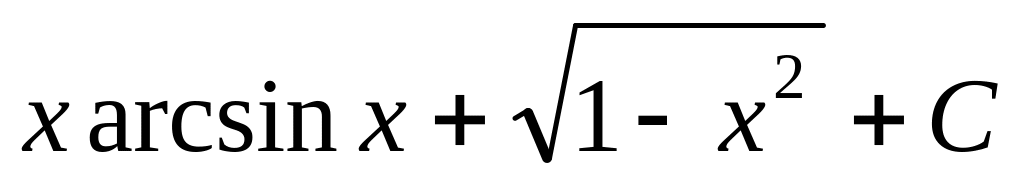 .
. Відповідь.
Відповідь.
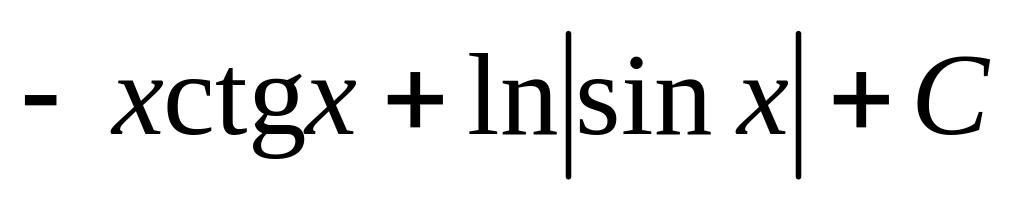 .
.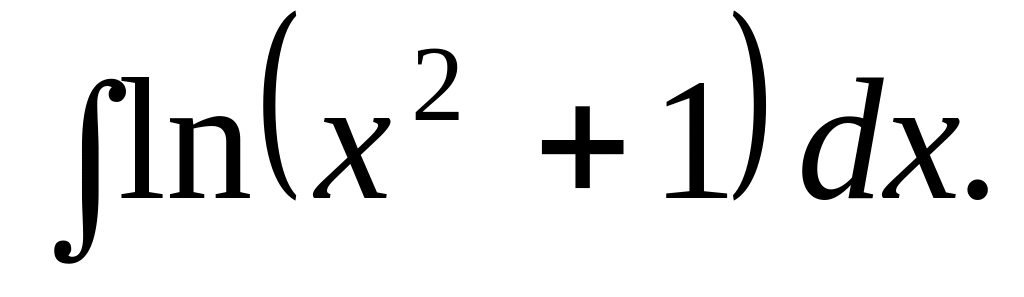 Відповідь.
Відповідь.
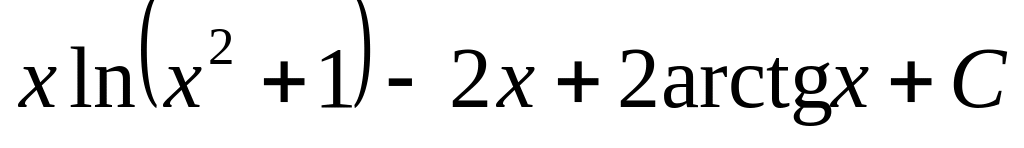 .
.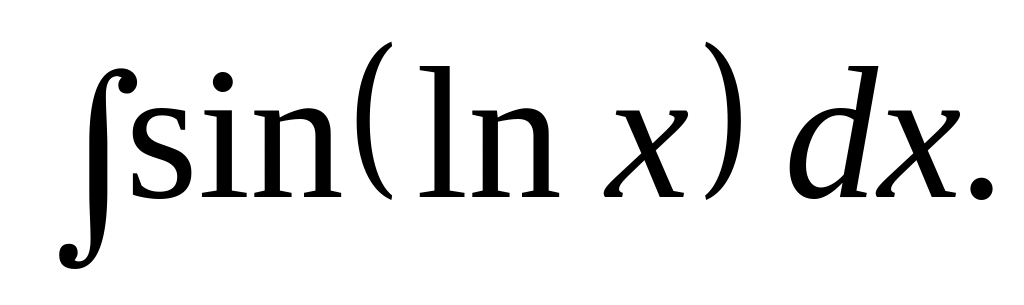 Відповідь.
Відповідь.
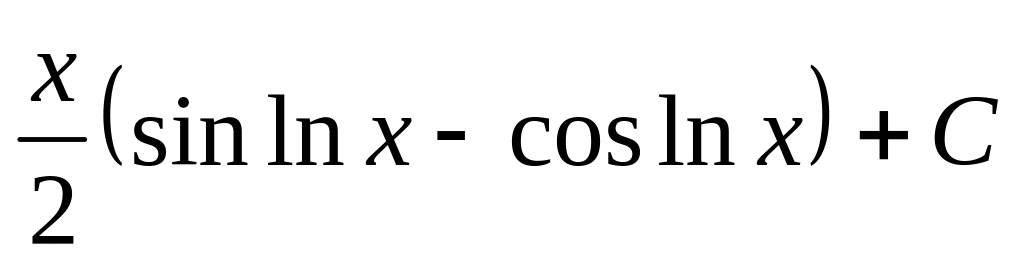 .
.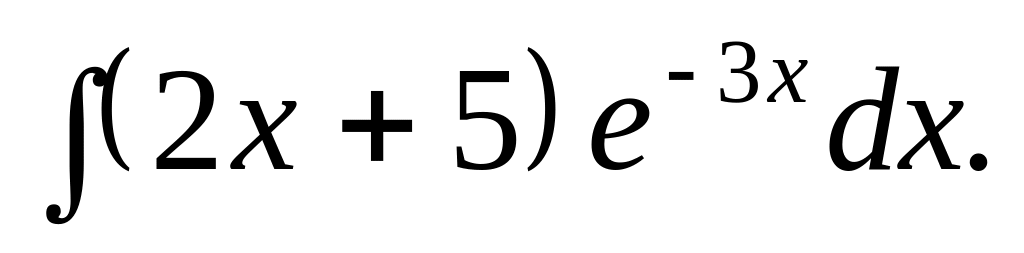 Відповідь.
Відповідь.
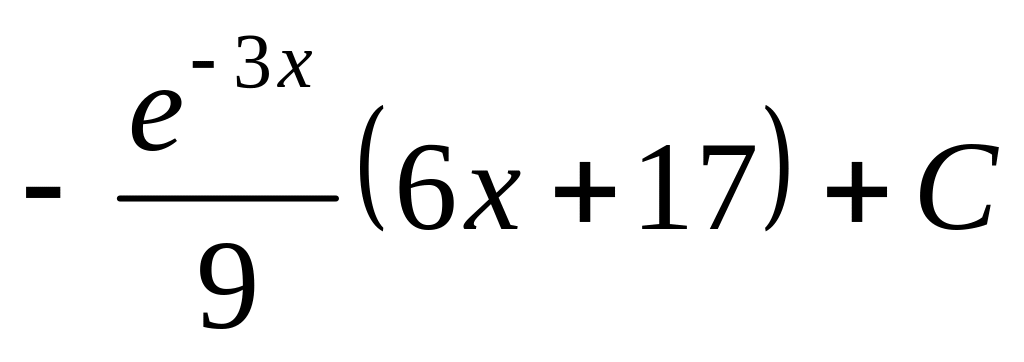 .
. Відповідь.
Відповідь.
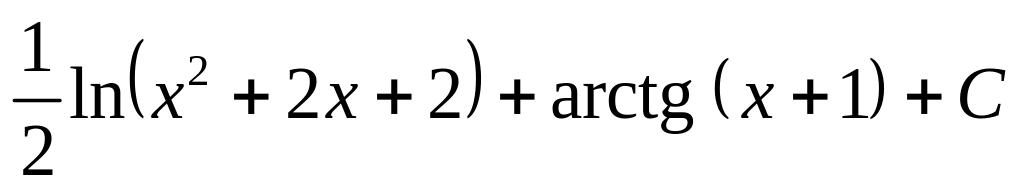 .
.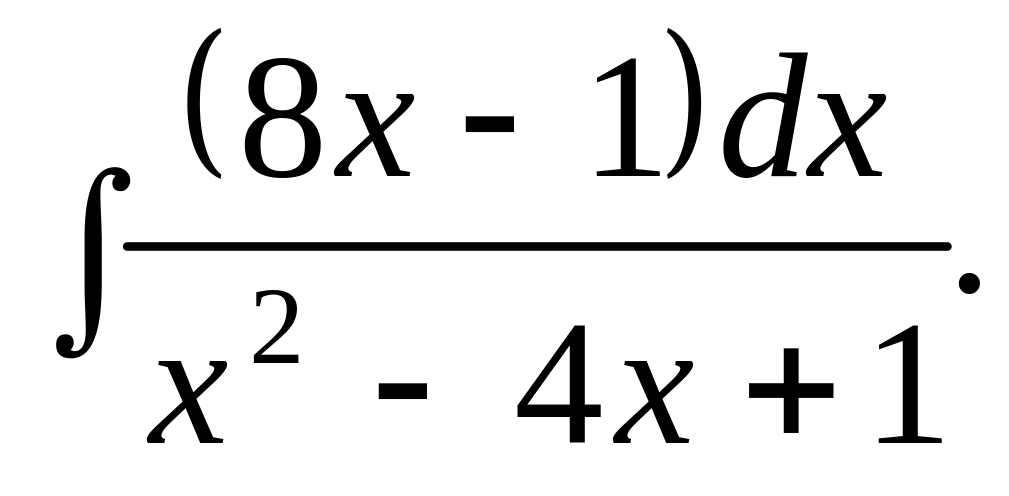 Відповідь.
Відповідь.
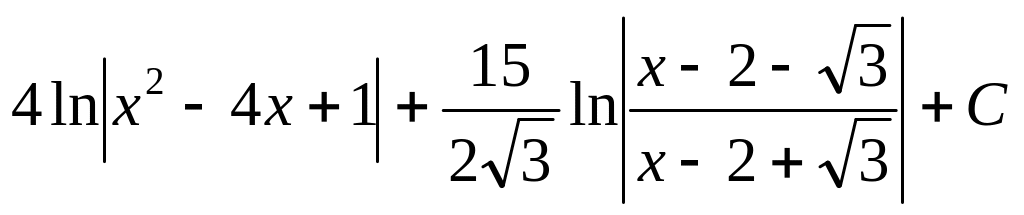 .
.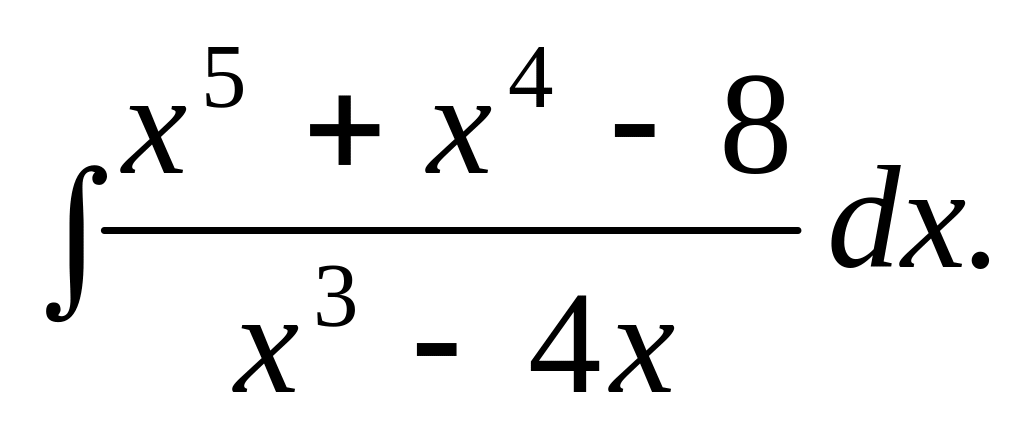 Відповідь.
Відповідь.
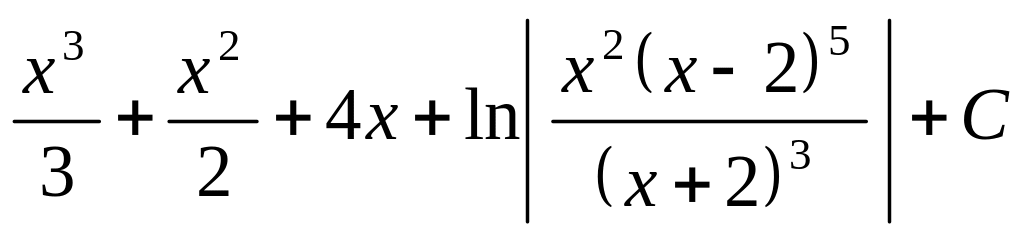 .
.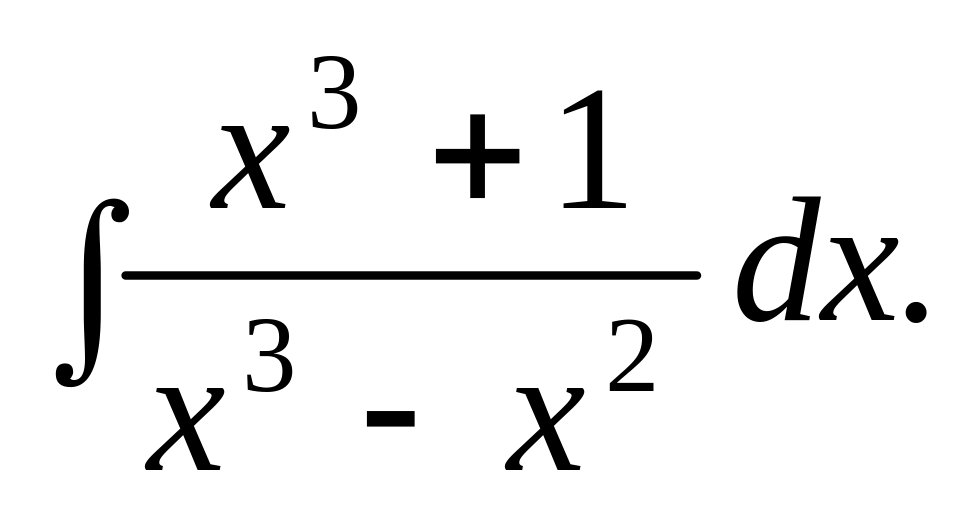 Відповідь.
Відповідь.
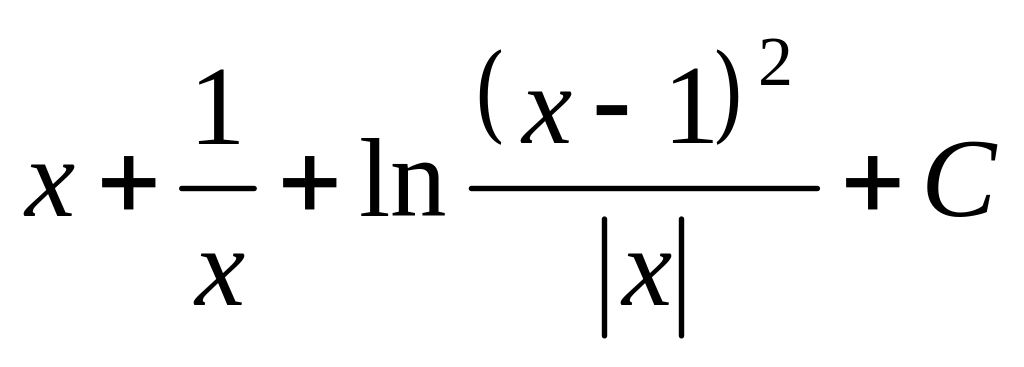 .
.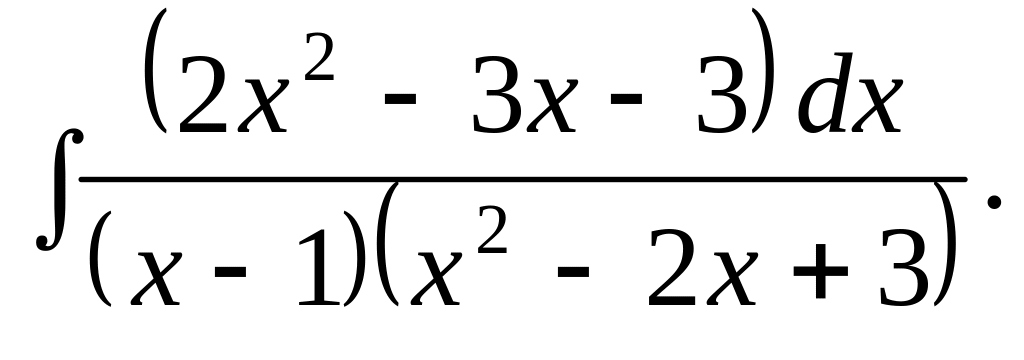 Відповідь.
Відповідь.
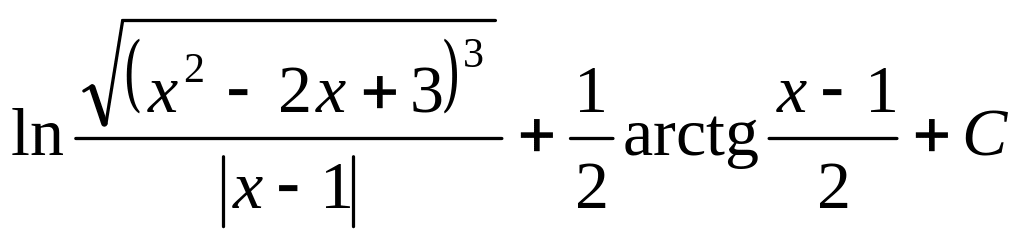 .
. Відповідь.
Відповідь.
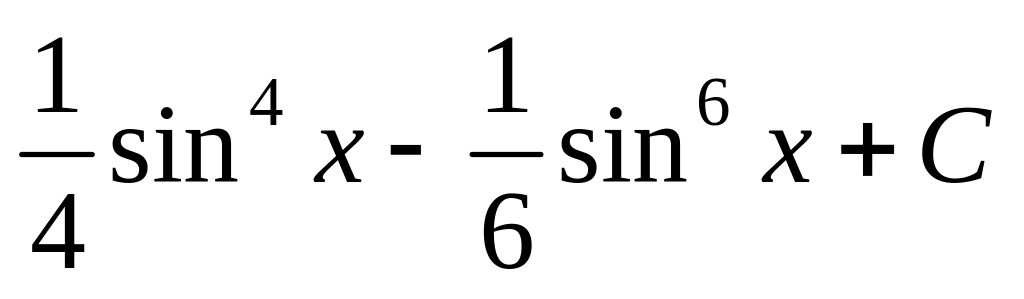 .
.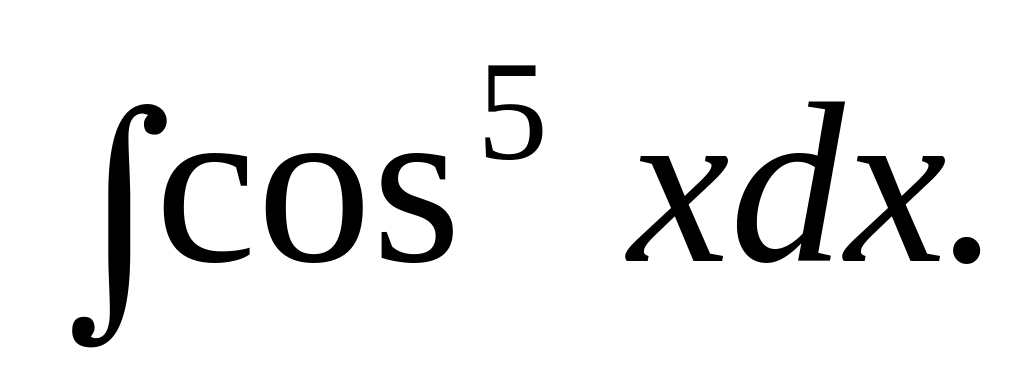 Відповідь.
Відповідь.
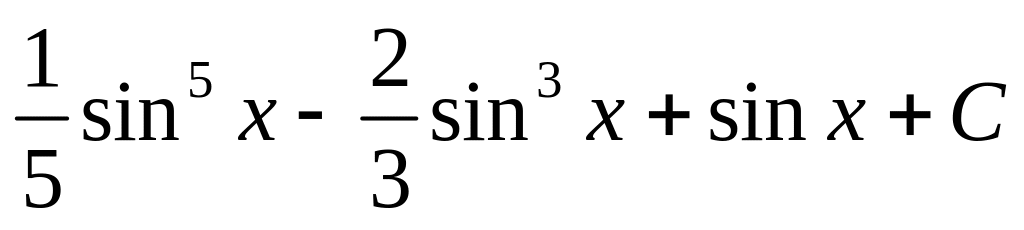 .
.
Завдання для
самостійної роботи: № 1-3; 7; 8; 10.
Практичне заняття № 7
Обчислення визначених інтегралів
План
Обчислення визначених інтегралів.
Знаходження площ плоских фігур.
Термінологічний словник ключових понять
Криволінійна трапеція — плоска фігура, що обмежена лініями:
![]() ,
у
= 0, х
= а,
х
= b.
,
у
= 0, х
= а,
х
= b.
Інтегральна
сума
—
сума виду
![]() .
.
Визначений
інтеграл
—
границя інтегральної суми при
![]() (7.8).
(7.8).
Інтегровна функція — функція, для якої існує визначений інтеграл.
Визначений
інтеграл зі змінною верхньою межею
інтегрування —
інтеграл виду
![]() .
.
Навчальні завдання
1.

![]()
![]() .
.
2.
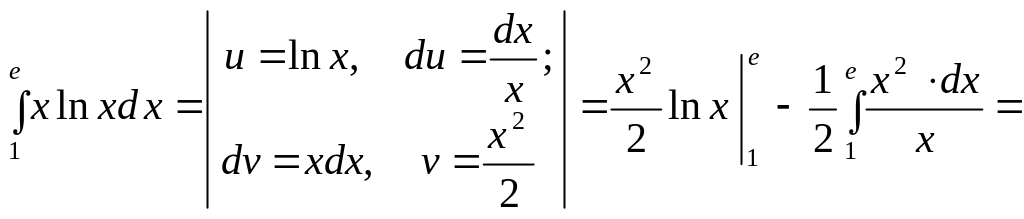
![]()
3.
Обчислити
площу фігури, обмеженої лініями
![]()
![]() .
.
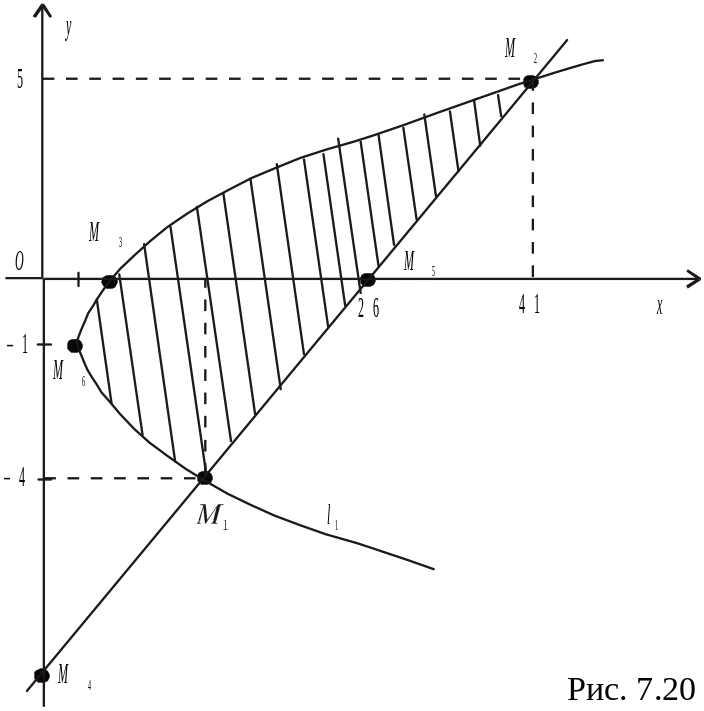
Побудуємо
фігуру, обмежену параболою
![]() та прямою
та прямою
![]() ,
на координатній площині; при цьому
обов’язково треба знайти точки
перетину заданих ліній між собою та з
осями координат (рис. 7.20)
,
на координатній площині; при цьому
обов’язково треба знайти точки
перетину заданих ліній між собою та з
осями координат (рис. 7.20)
![]()
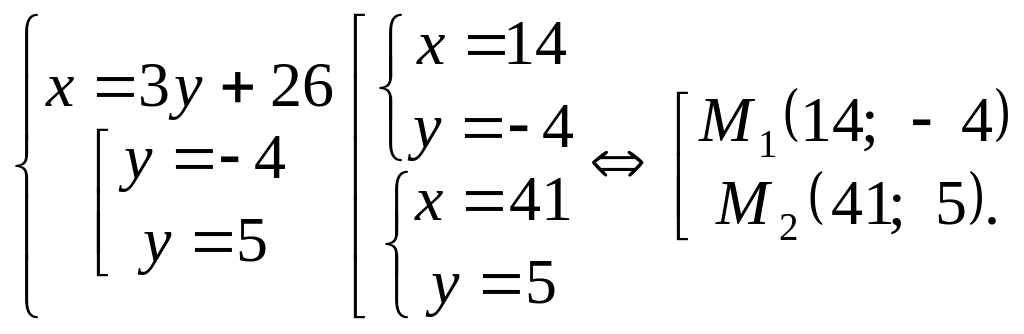
![]() .
.
![]() .
.
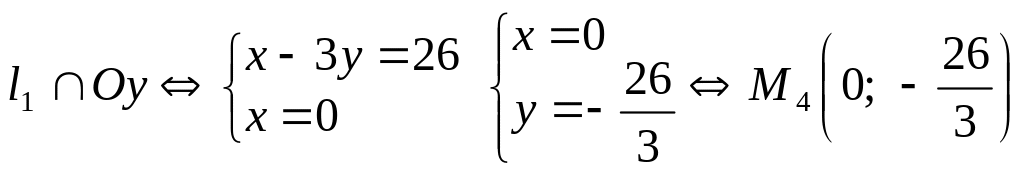 .
.
![]() .
.
![]() —
вершина
параболи.
—
вершина
параболи.
Для
обчислення площі фігури
![]() найбільш зручно скористатись формулою
найбільш зручно скористатись формулою
![]() .
.
Отже, за цією формулою дістанемо:
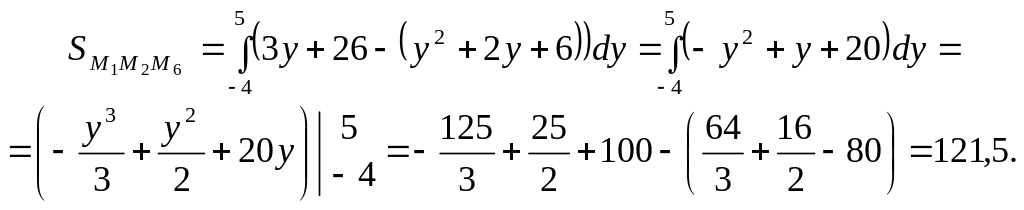
Завдання для перевірки знань
Обчислити визначені інтеграли:
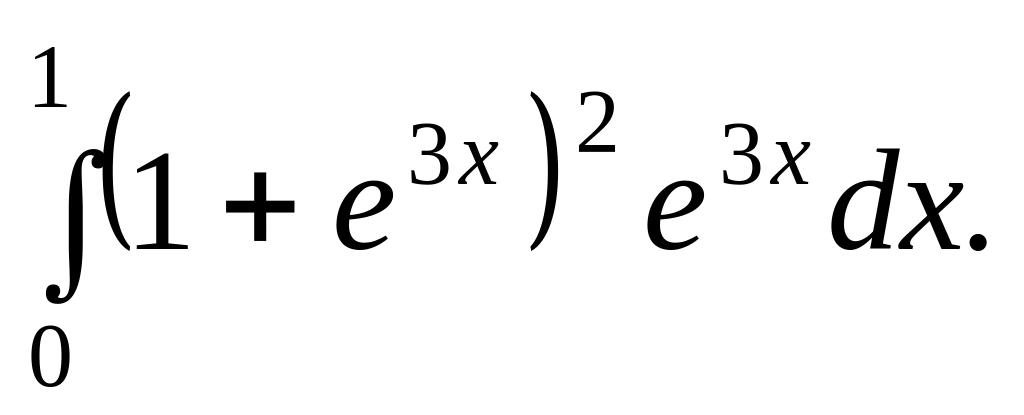 Відповідь.
Відповідь.
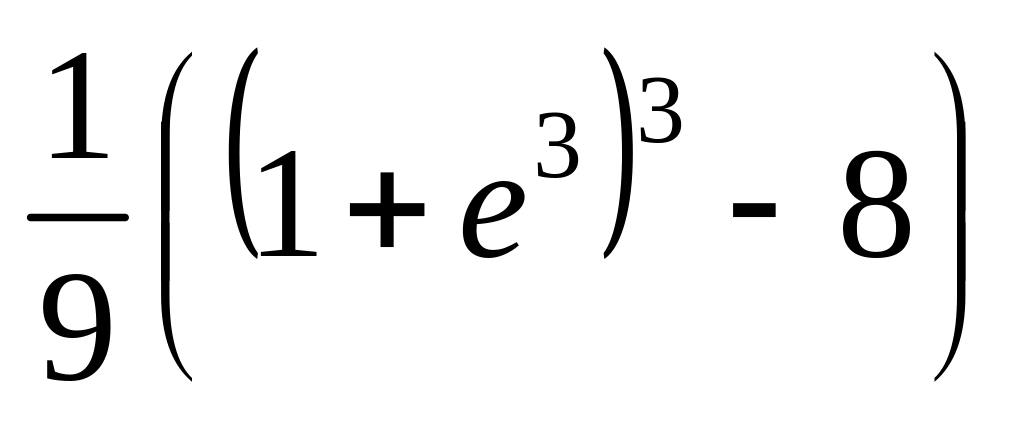 .
.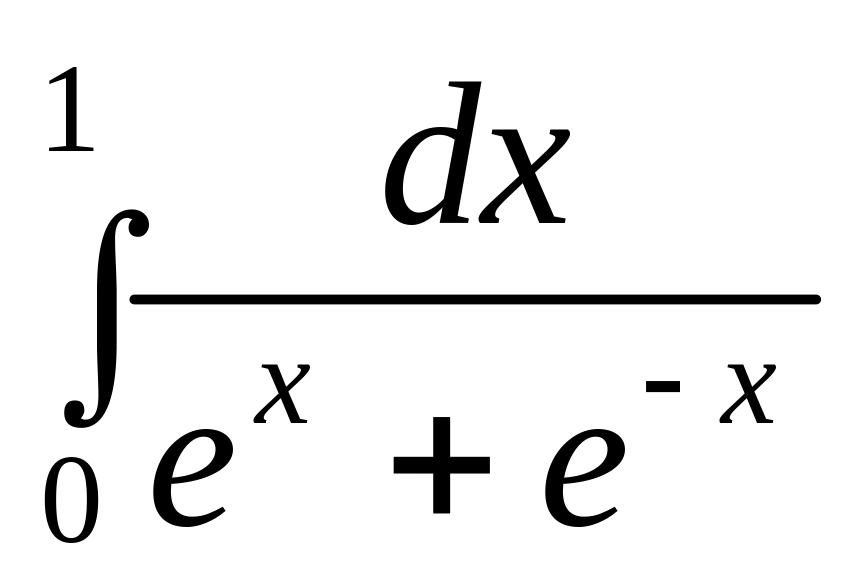 .
Відповідь.
.
Відповідь.
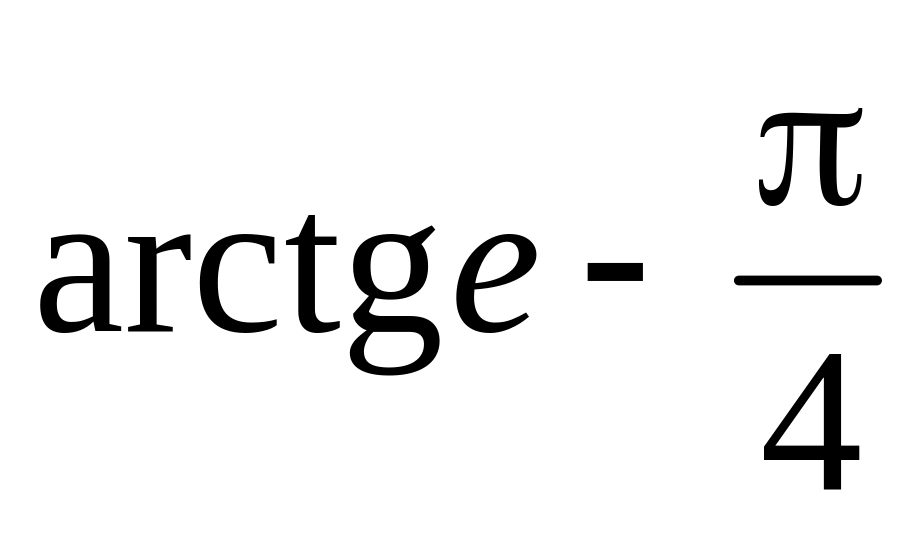 .
.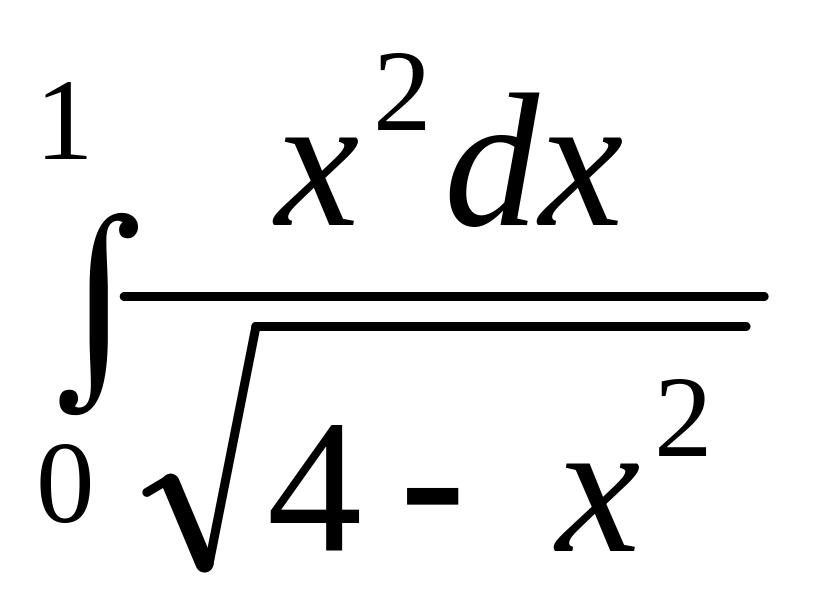 .
Відповідь.
.
Відповідь.
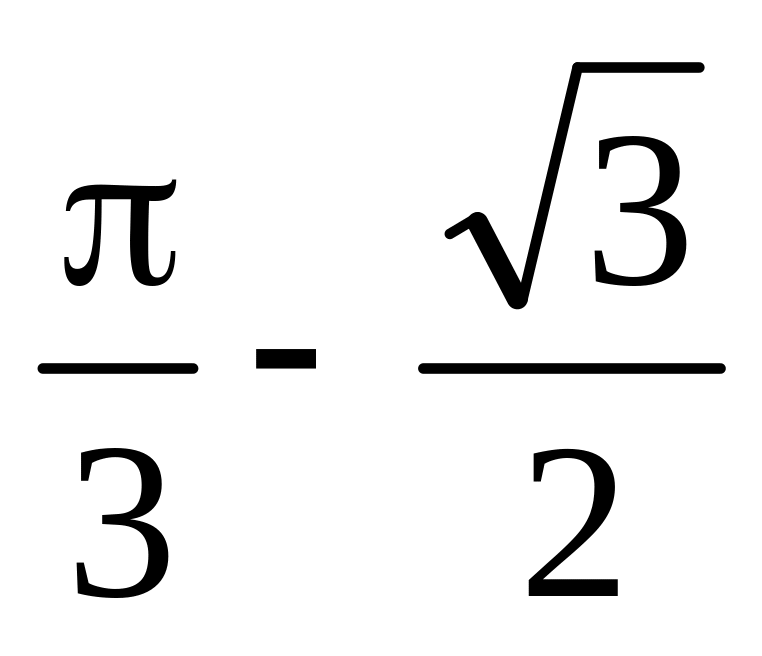 .
.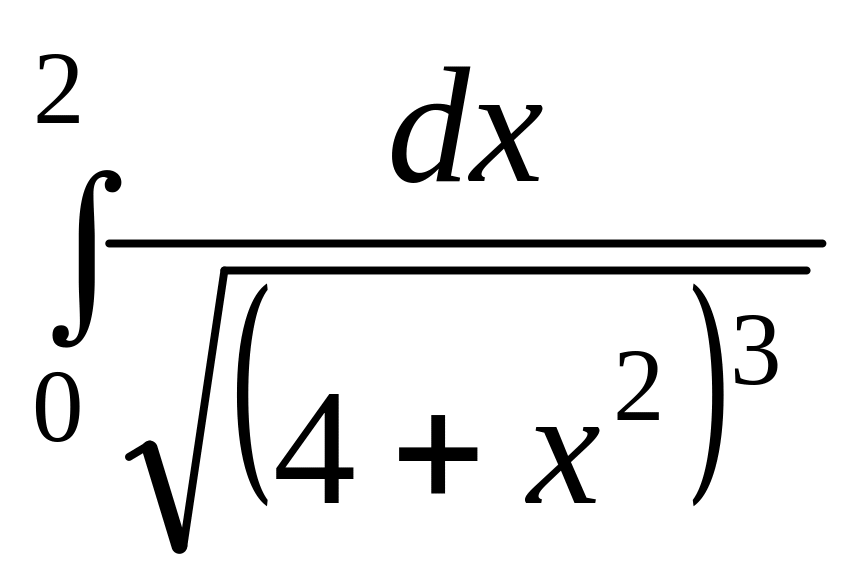 .
Відповідь.
.
Відповідь.
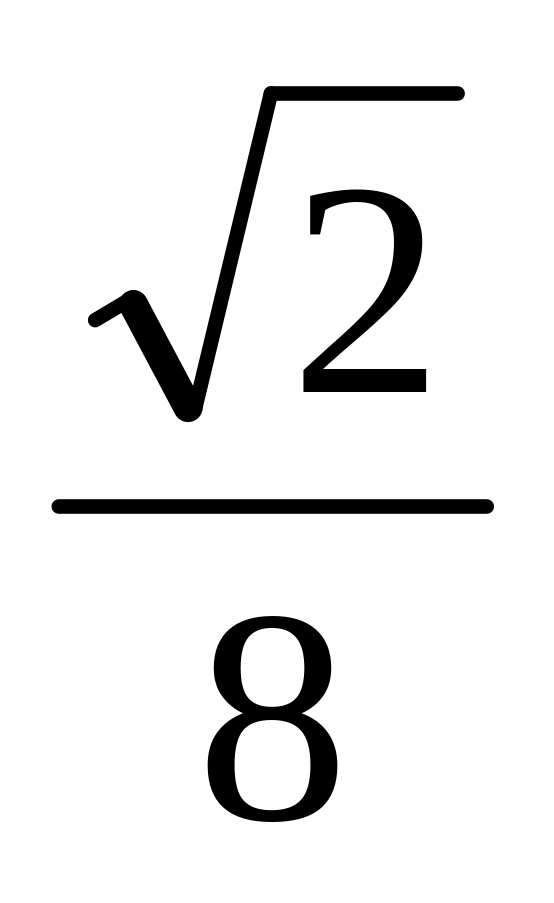 .
.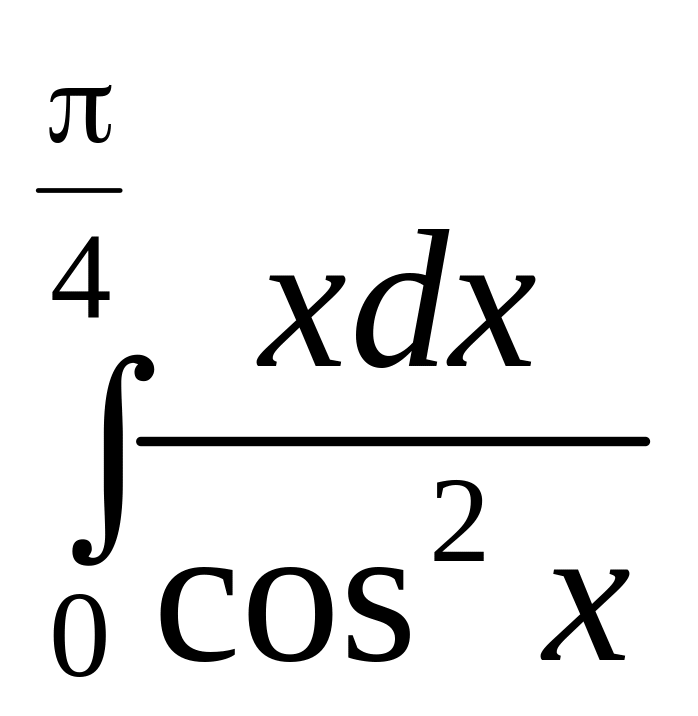 .
Відповідь.
.
Відповідь.
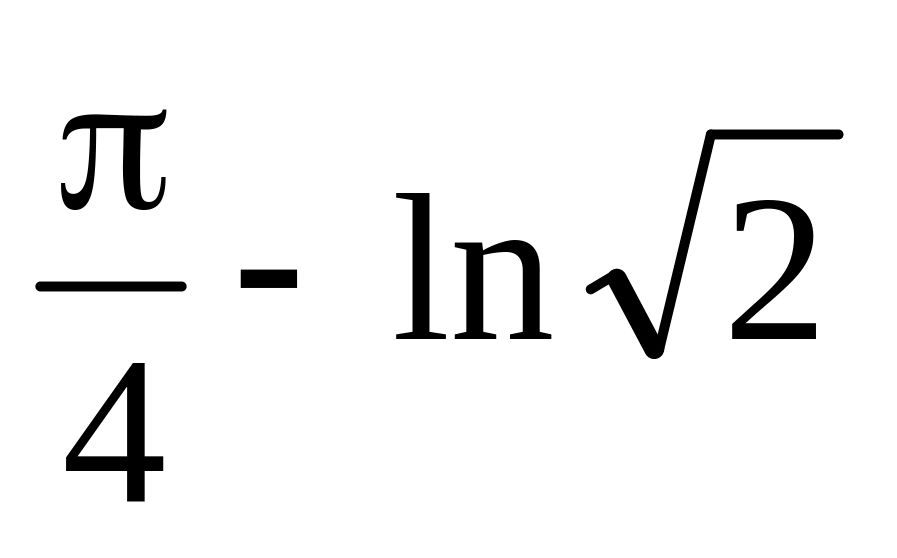 .
.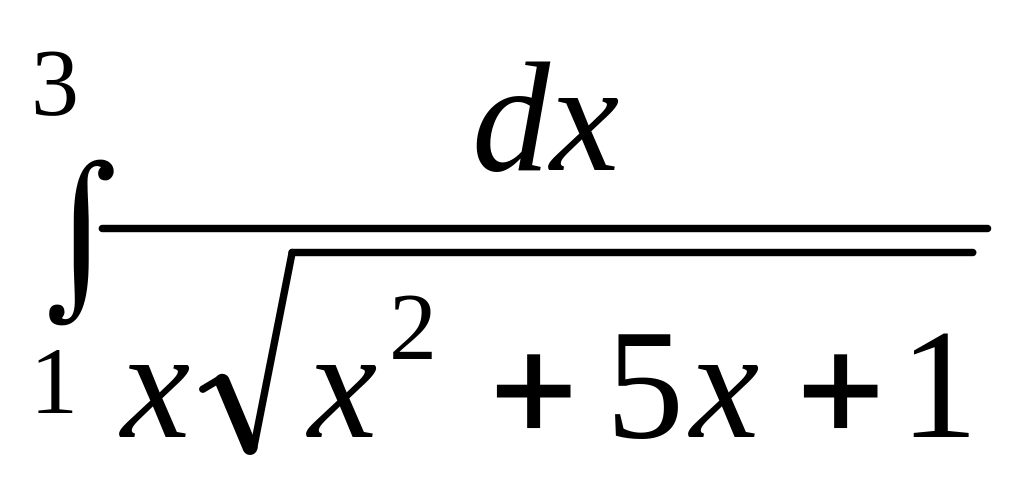 .
Відповідь.
.
Відповідь.
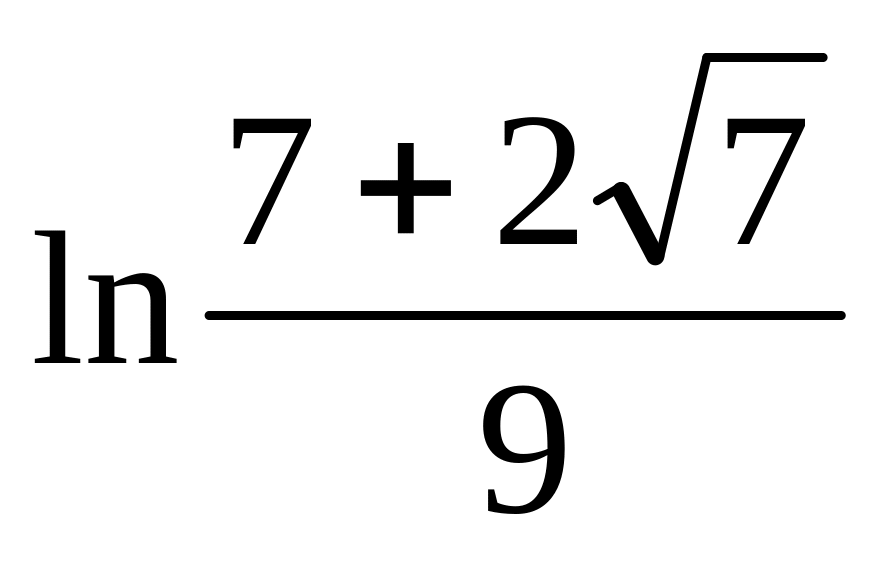 .
.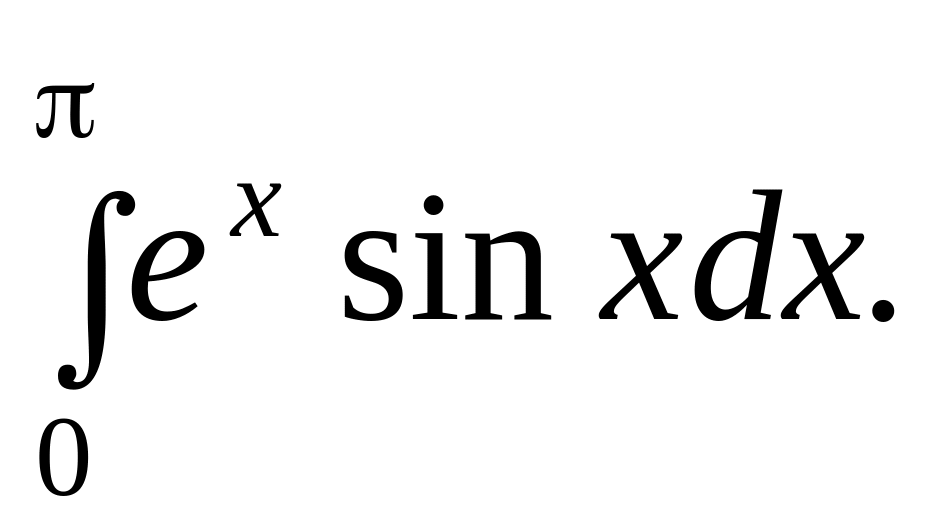 Відповідь.
Відповідь.
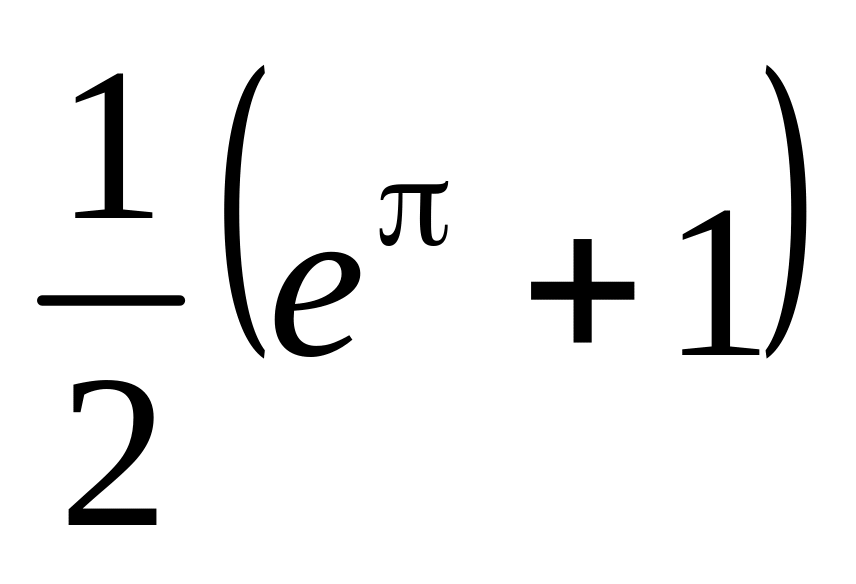 .
.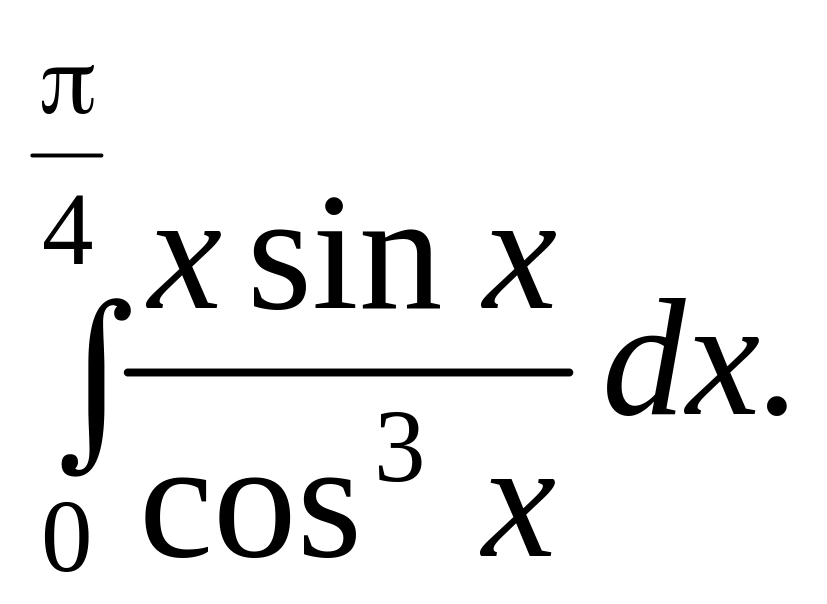 Відповідь.
Відповідь.
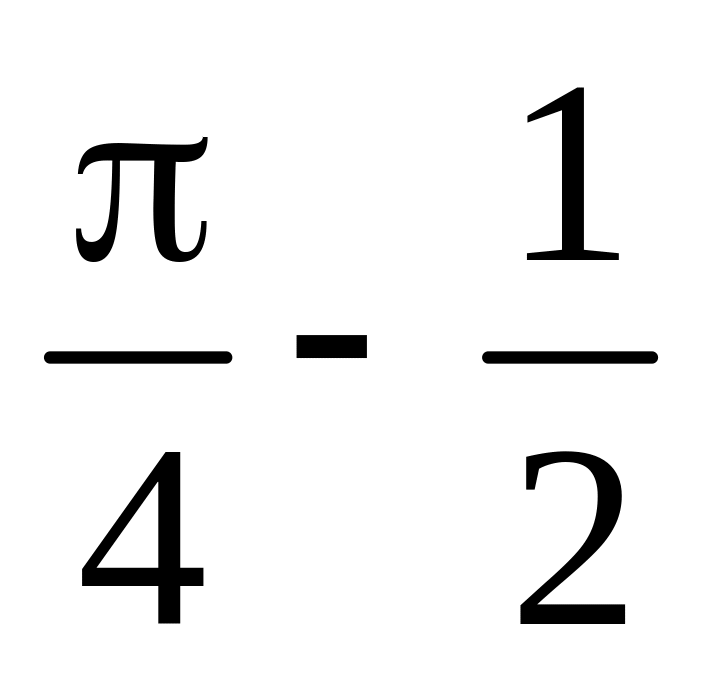 .
.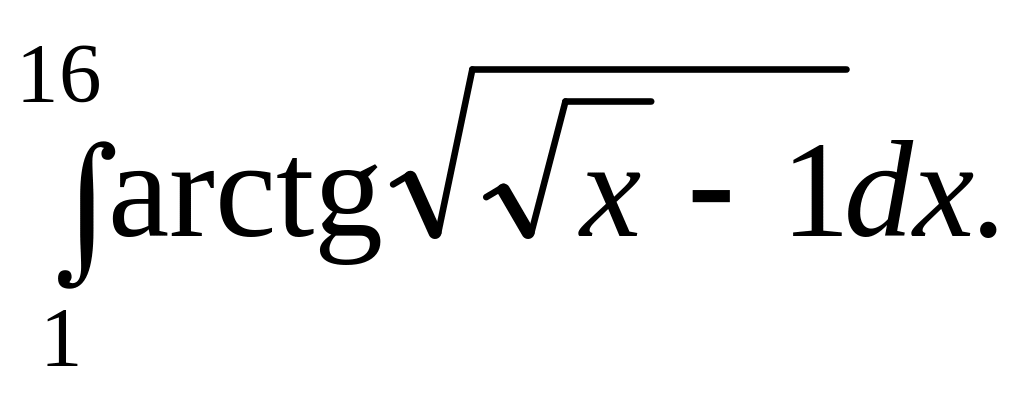 Відповідь.
Відповідь.
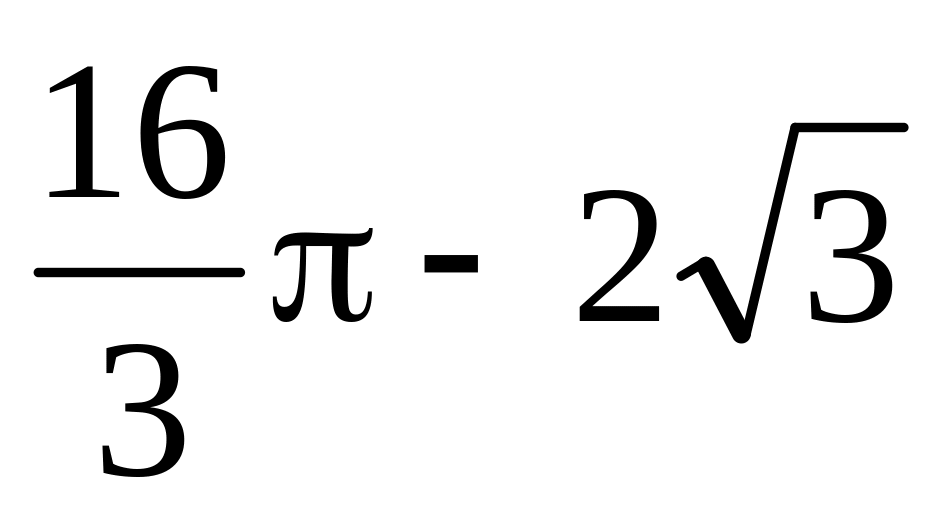 .
.
Обчислити площу фігури, обмеженої лініями.
 ,
,
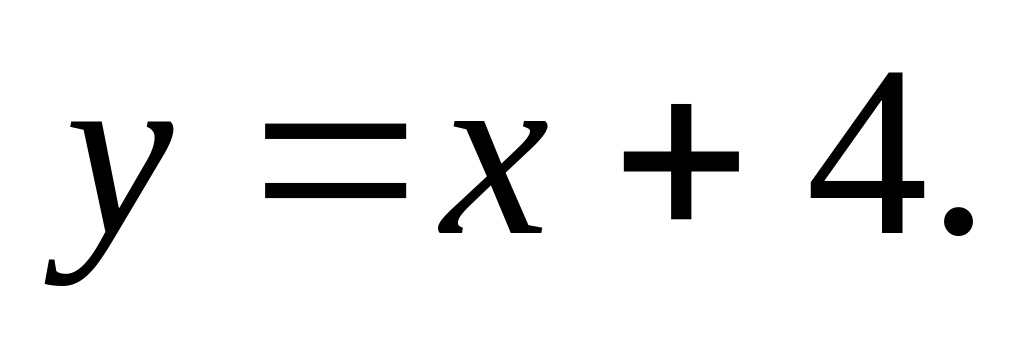 Відповідь.
Відповідь.
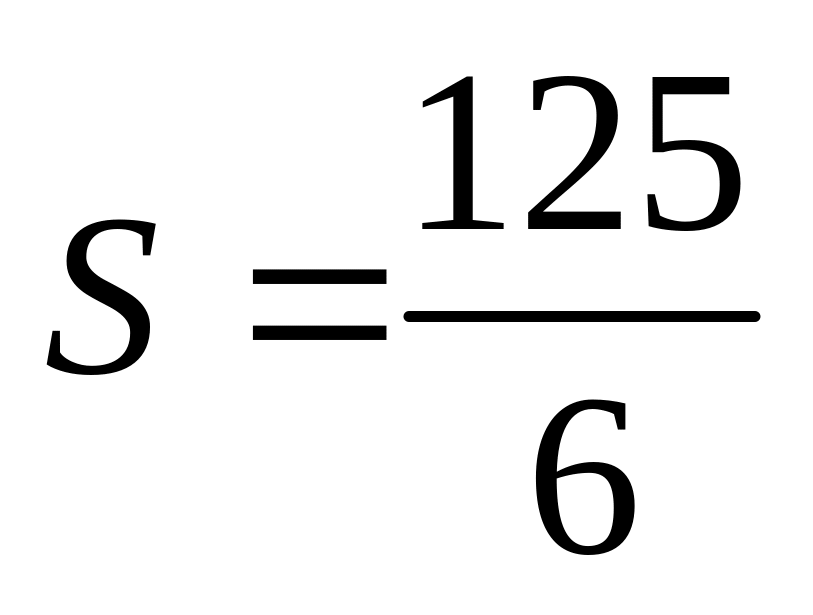 .
.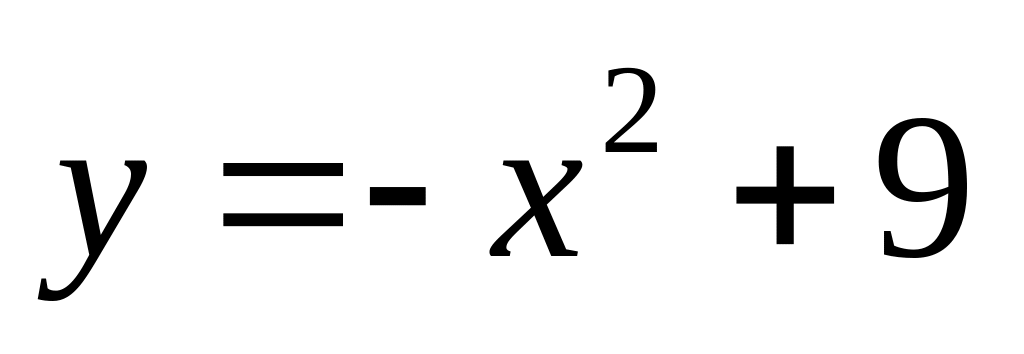 ,
,
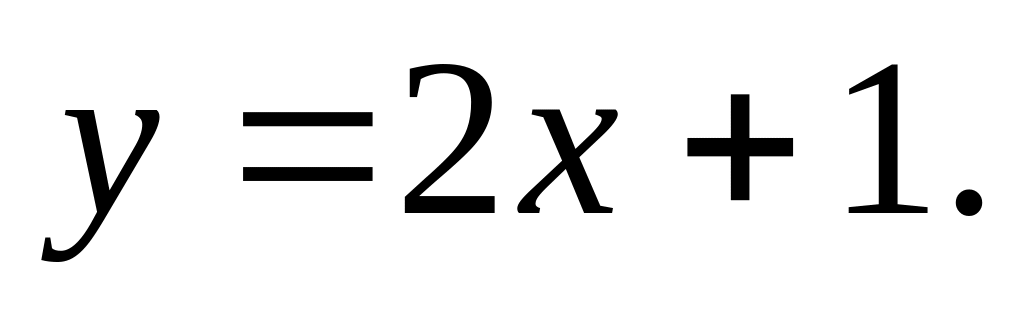 Відповідь.
Відповідь.
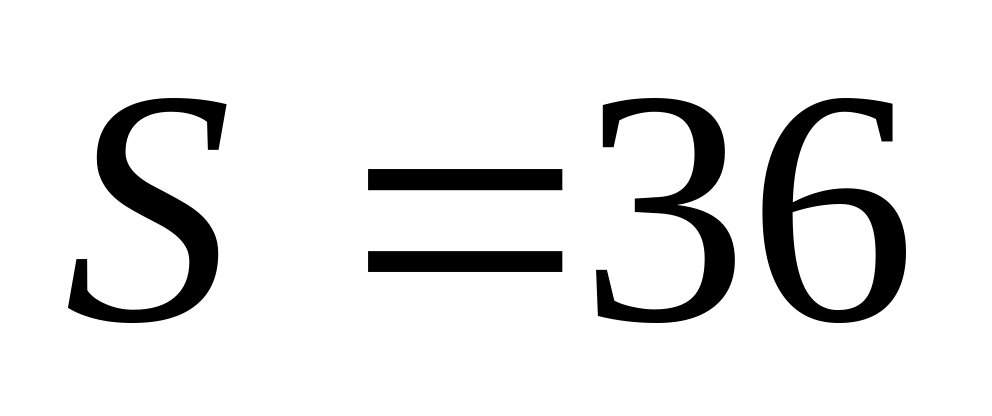 .
.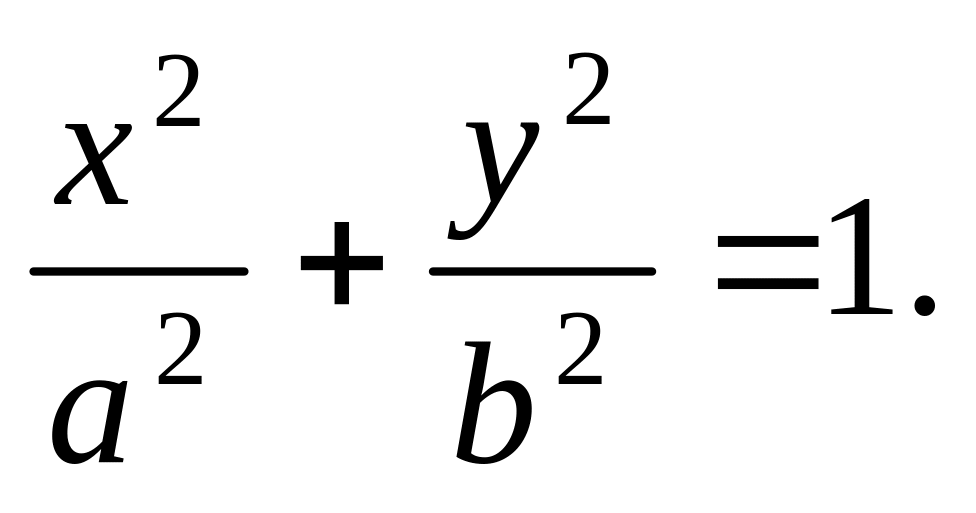 Відповідь.
Відповідь.
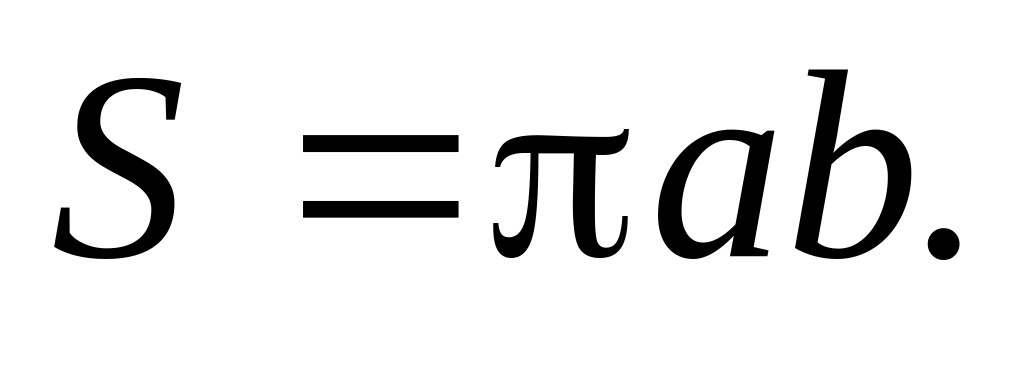
 ,
,
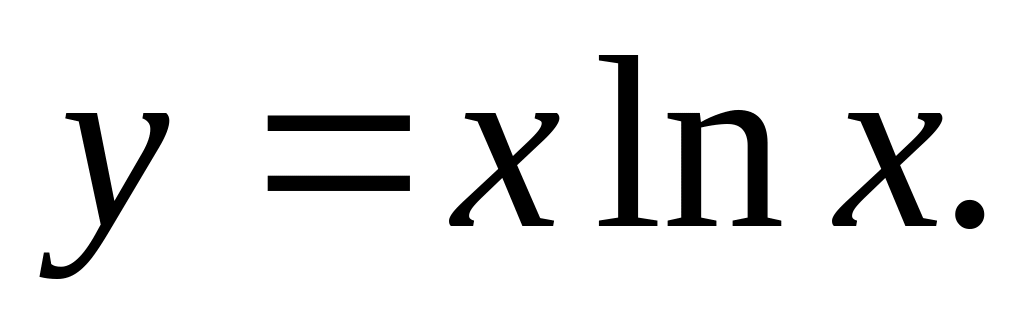 Відповідь.
Відповідь.
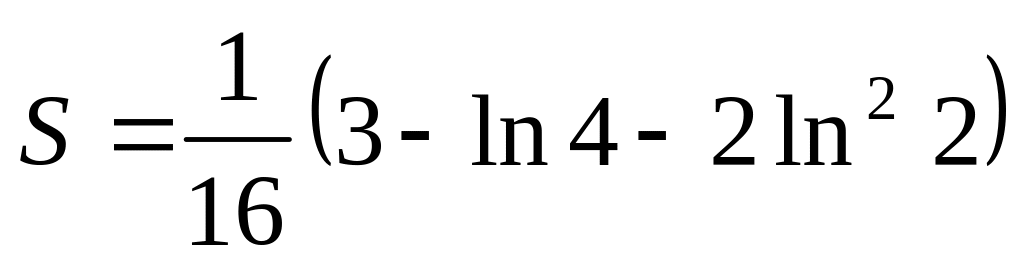 .
.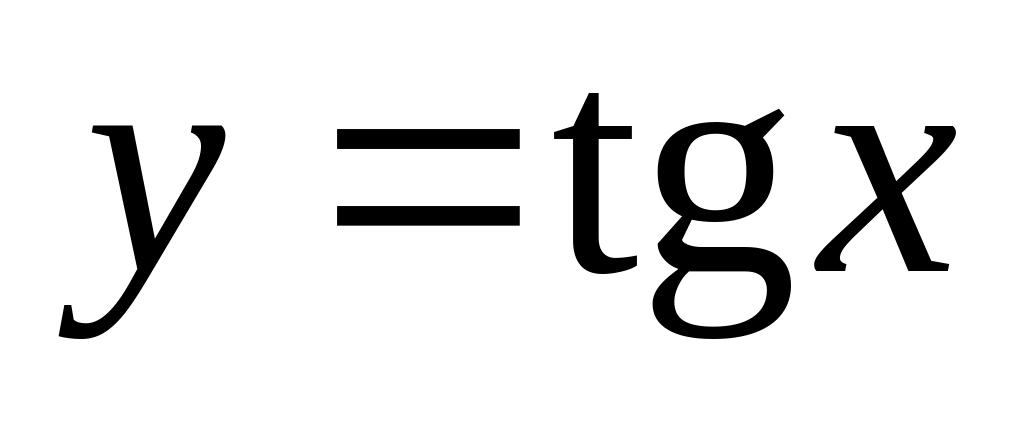 ,
,
 Відповідь.
Відповідь.
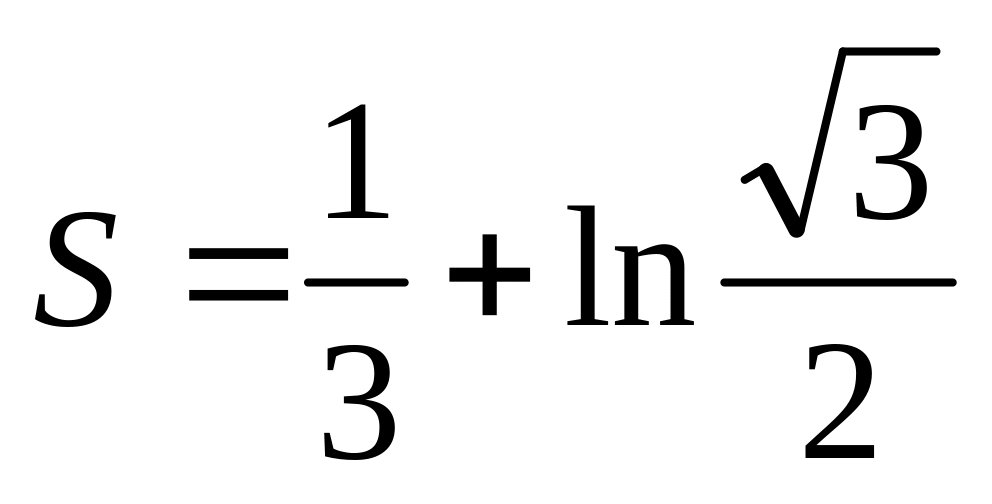 .
.
Завдання для
самостійної роботи: № І (1-3); ІІ (1-3).
Практичне заняття № 8-9 Диференціальні рівняння План
1. Диференціальні рівняння. Загальний і частинний розв’язок.
2. Диференціальні рівняння першого порядку з відокремлюваними змінними. Однорідні рівняння.
3. Диференціальні рівняння в повних диференціалах. Лінійні диференціальні рівняння.
4. Зниження порядку диференціальних рівнянь другого порядку.
Термінологічний словник ключових понять
Частинний (загальний) розв’язок диференціального рівняння — розв’язок диференціального рівняння, що не містить (містить) довільної сталої.
Задача Коші — задача пошуку розв’язку із заданими початковими умовами.
Диференціальні рівняння з відокремлюваними змінними — рівняння, в якому можна відокремити змінні.
Диференціальні однорідні рівняння — рівняння першого порядку з однорідною правою частиною.
Диференціальні рівняння в повних диференціалах — диференціальні рівняння, що визначаються повним диференціалом деякою функцією.
Лінійні диференціальні рівняння — рівняння лінійно залежить від невідомої функції і її похідної.
