
- •Методичні вказівки до проведення практичних робіт
- •Практичне заняття № 1 Обчислення визначників План
- •Навчальні завдання
- •Завдання для перевірки знань
- •Практичне заняття № 2 Матриці План
- •Термінологічний словник ключових понять
- •Навчальні завдання
- •Завдання для перевірки знань
- •Практичне заняття № 3 Вектори
- •1. Лінійні операції з векторами.
- •2. Застосування скалярного, векторного і мішаного добутків векторів для розв’язування задач. Термінологічний словник ключових понять
- •Навчальні завдання
- •Завдання для перевірки знань
- •Практичне заняття № 4 Прямі на площині і в просторі План
- •Термінологічний словник ключових понять
- •Навчальні завдання
- •Завдання для перевірки знань
- •Практичне заняття № 5 Криві другого порядку План
- •Завдання для перевірки знань
- •Завдання для перевірки знань
- •Термінологічний словник ключових понять
- •Навчальні завдання
- •Завдання для перевірки знань
- •Обчислення визначених інтегралів
- •Завдання для перевірки знань
- •Практичне заняття № 8-9 Диференціальні рівняння План
- •Термінологічний словник ключових понять
- •Навчальні завдання
- •Завдання для перевірки знань
Завдання для перевірки знань
1. Обчислити добутки матриць:
а)
![]() ; б)
; б)
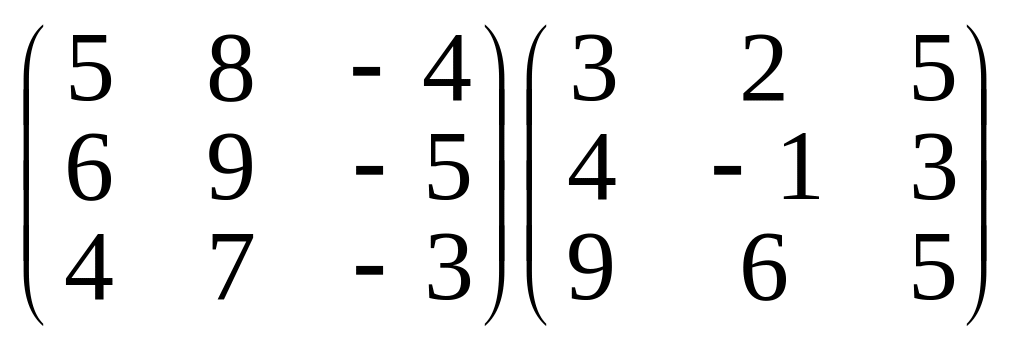 ;
;
в)
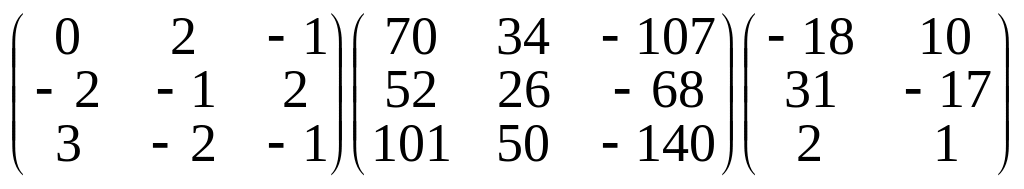 .
.
2.
Знайти
матрицю
![]() ,
якщо
,
якщо
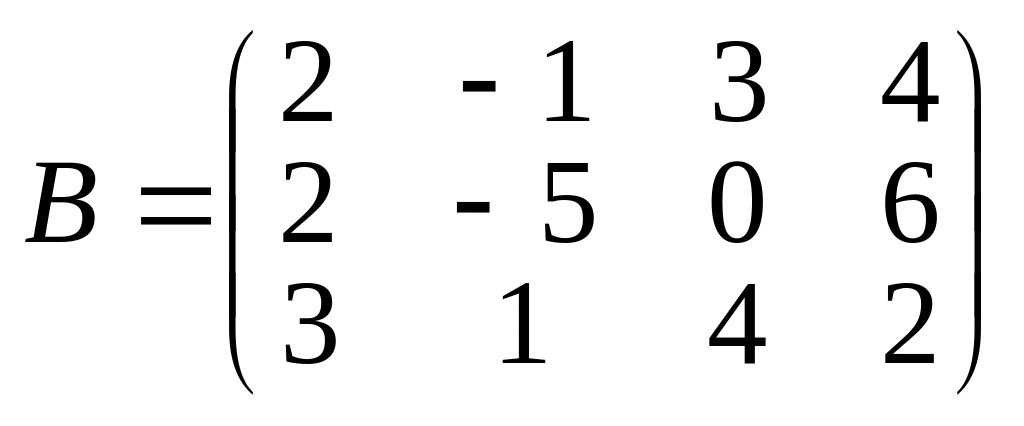 ;
;
 ;
;
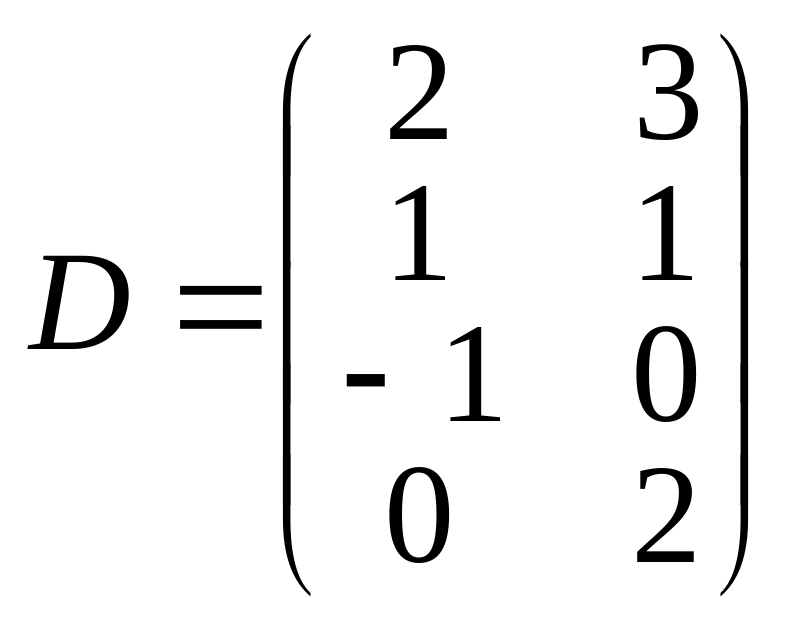 .
.
3.
а)
![]() ;
б)
;
б)
![]() .
.
Відповідь.
а)
![]() ;
б)
;
б)
![]() ,
якщо
,
якщо
![]() — парне;
— парне;
![]() ,
якщо
— непарне.
,
якщо
— непарне.
4. Знайти значення
![]() і
і
![]() ,
,
якщо
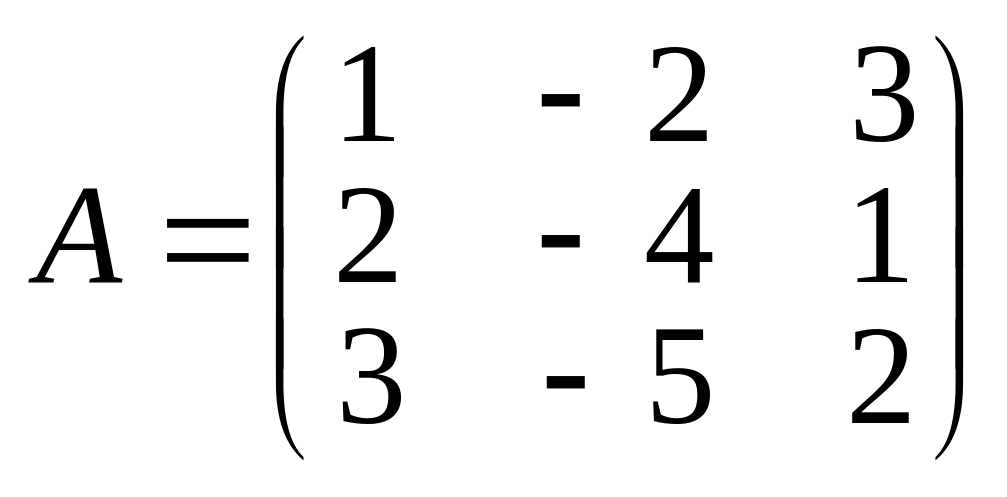 ;
;
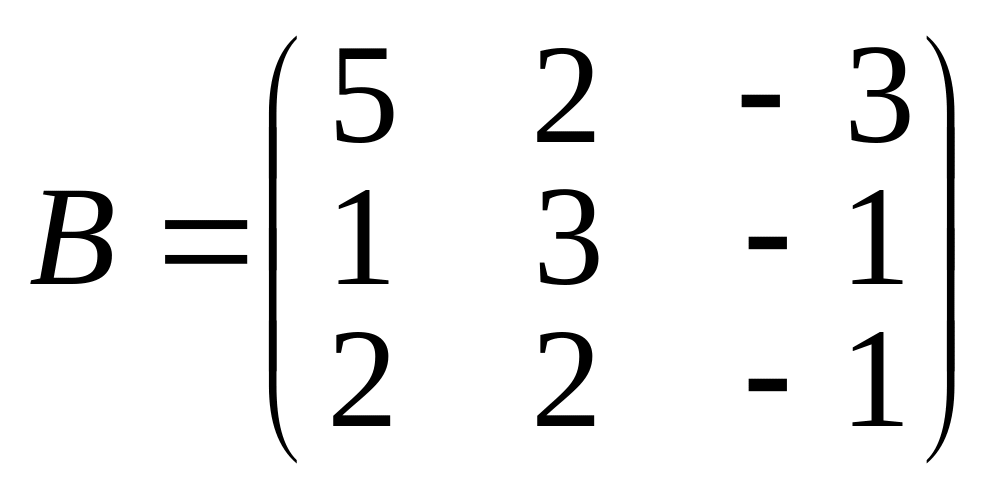 .
.
Відповідь.
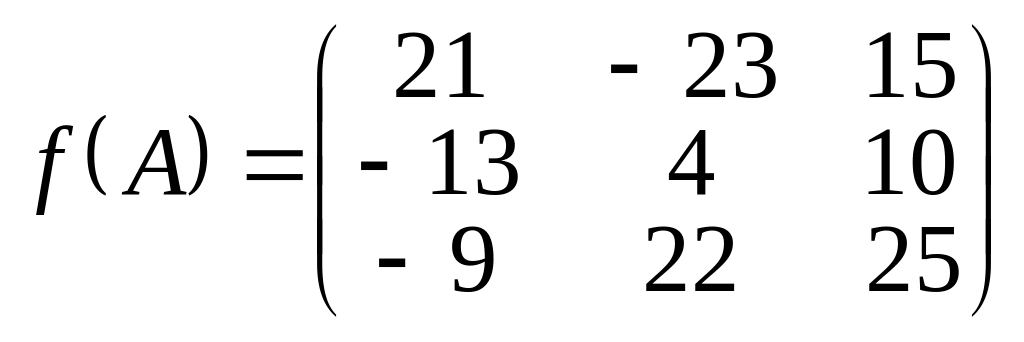 ;
;
 .
.
5.
Матриці А
і В
називаються переставними,
якщо
![]() .
Знайти всі матриці, переставні з
матрицями:
.
Знайти всі матриці, переставні з
матрицями:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
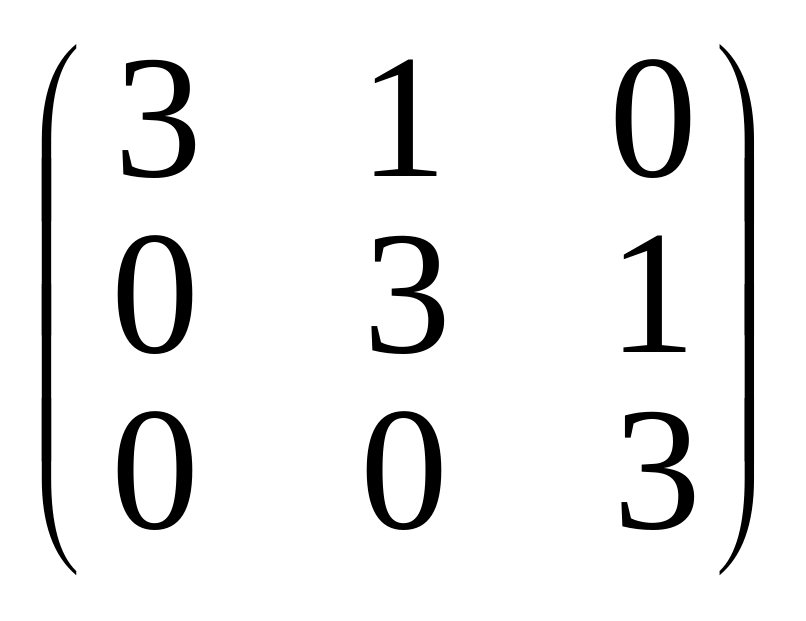 .
.
Відповідь.
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
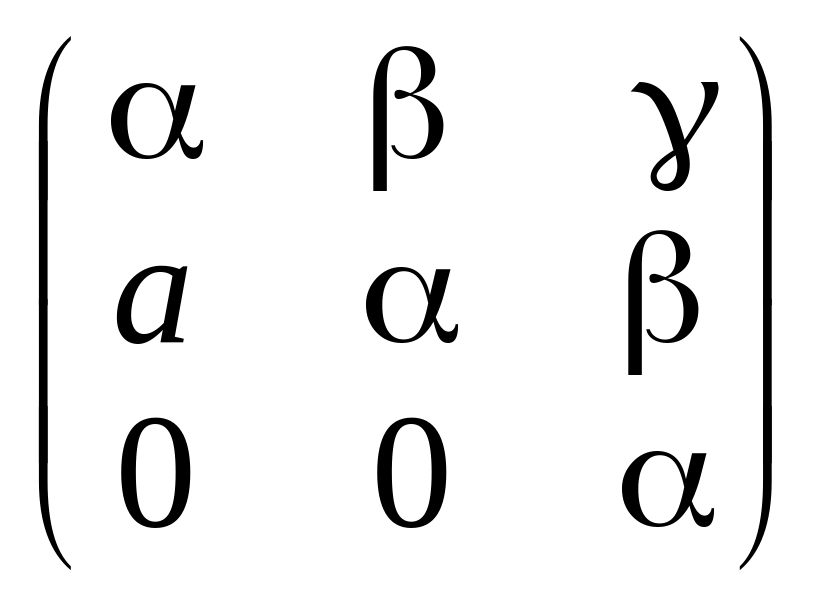 ,
де
,
де
![]() — будь-які
числа.
— будь-які
числа.
6. Знайти матриці, обернені до матриць:
а)
;
б)
![]() ;
в)
;
в)
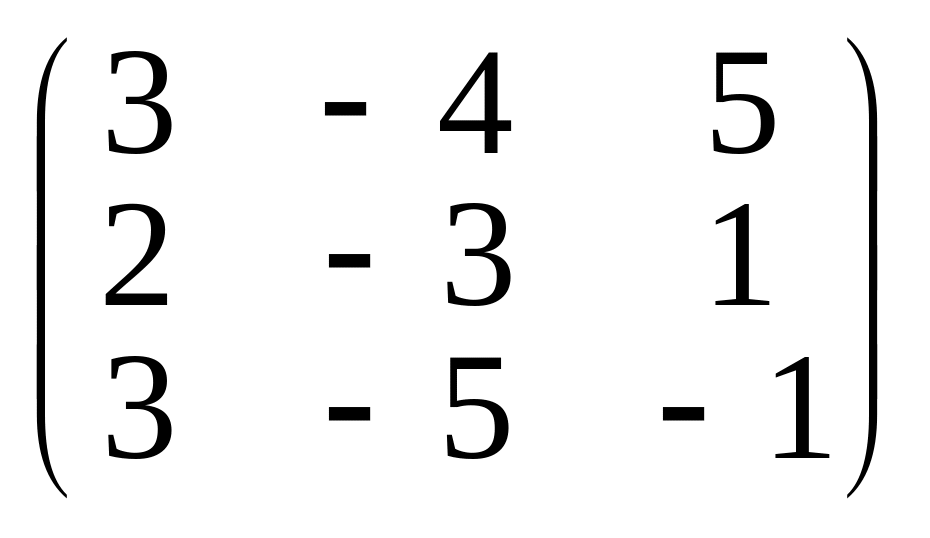 ;
г)
;
г)
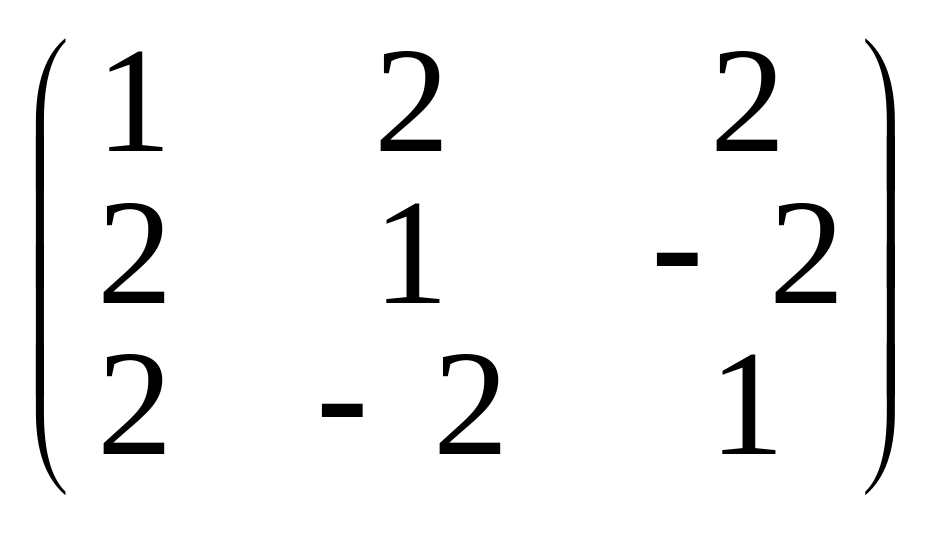 .
.
Результат перевірити множенням.
7. Розв’язати системи рівнянь методом оберненої матриці:
а)
![]() б)
б)
![]()
в)
![]() г)
г)
![]()
Відповідь. а) x1 = –1, x2 = 3, x3 = –2, x4 = 2; б) x1 = 2, x2 = 1, x3 = –3, x4 = 1; в) x1 = –3, x2 = 2, x3 = 1; г) x1 = 1, x2 = 1, x3 = 1.
8. Розв’язати матричні рівняння:
а)
![]() ;
б)
;
б)
![]() ;
;
в)
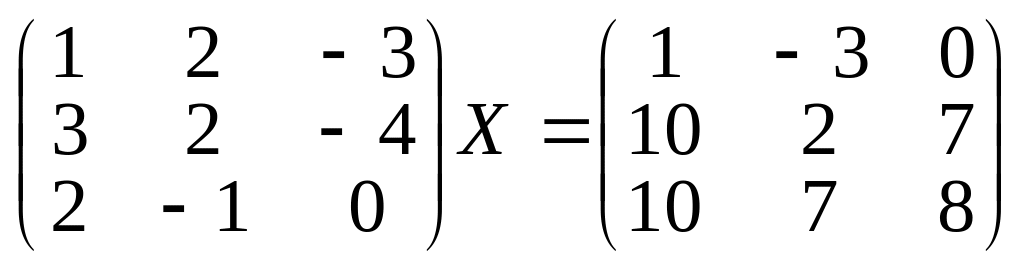 ;
г)
;
г)
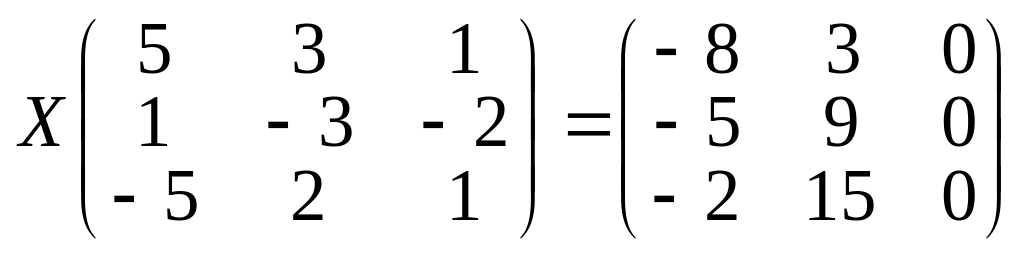 .
.
Відповідь.
а)
![]() ;
б)
;
в)
;
б)
;
в)
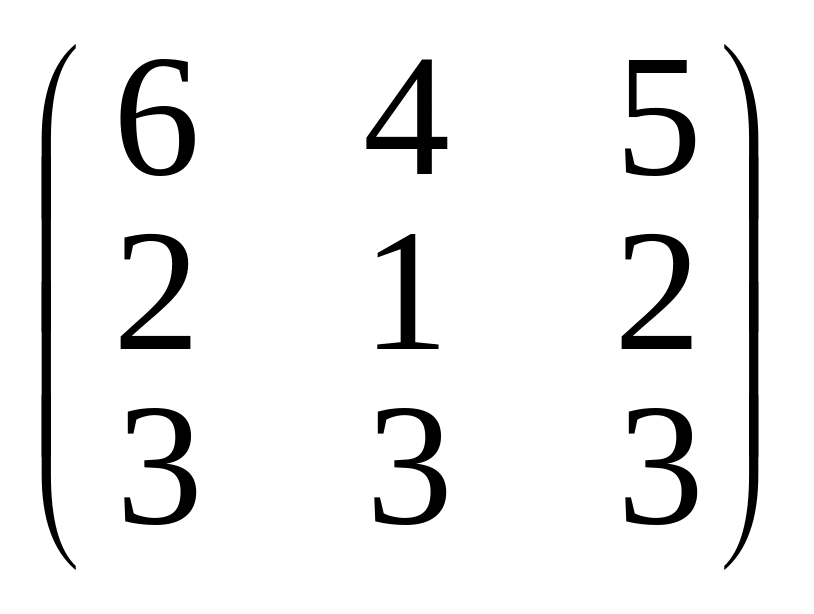 ;
г)
;
г)
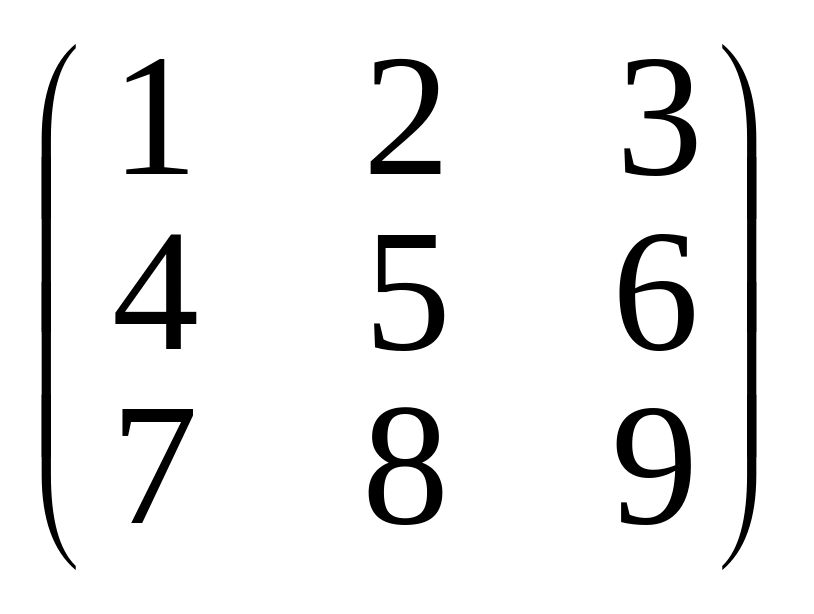 .
.
9. Знайти ранг матриць методом обвідних мінорів:
а)
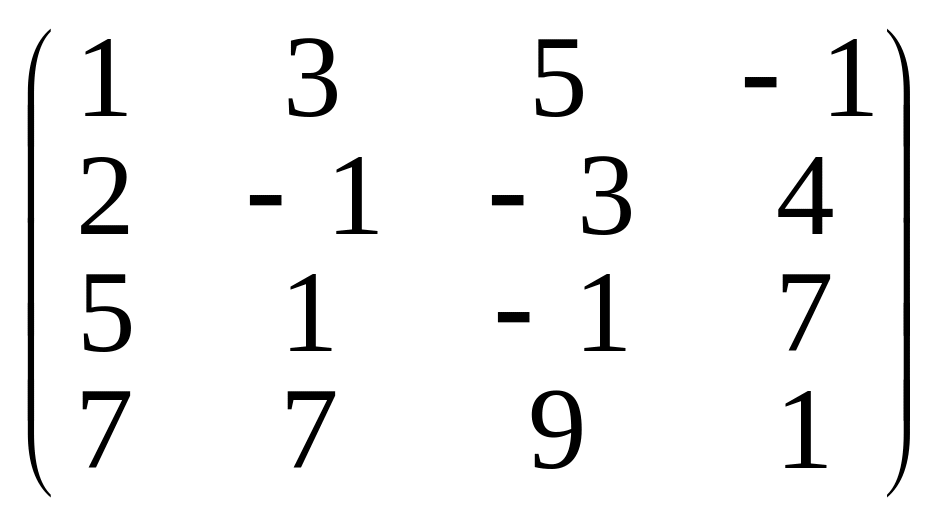 ;
б)
;
б)
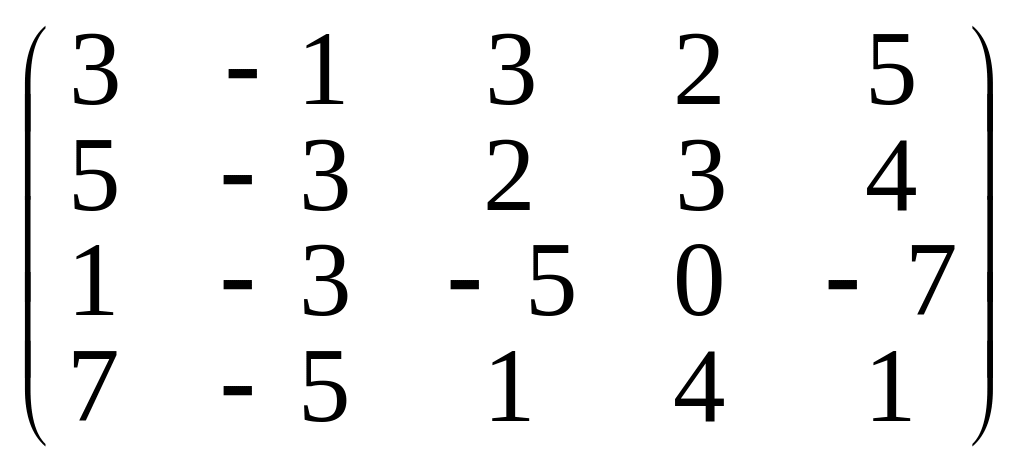 .
.
Відповідь. а) 3; б) 3.
10.
Дослідити залежно від значення
![]() ранг матриць:
ранг матриць:
а)
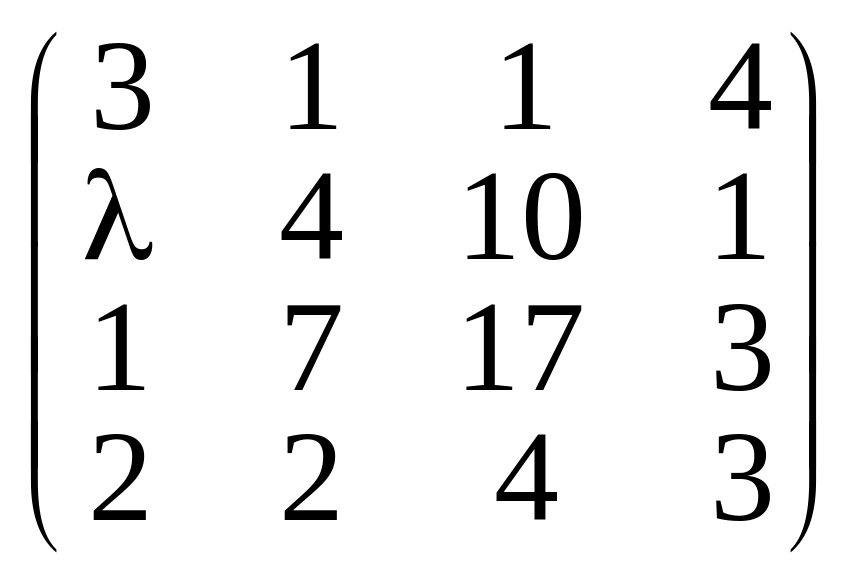 ;
б)
;
б)
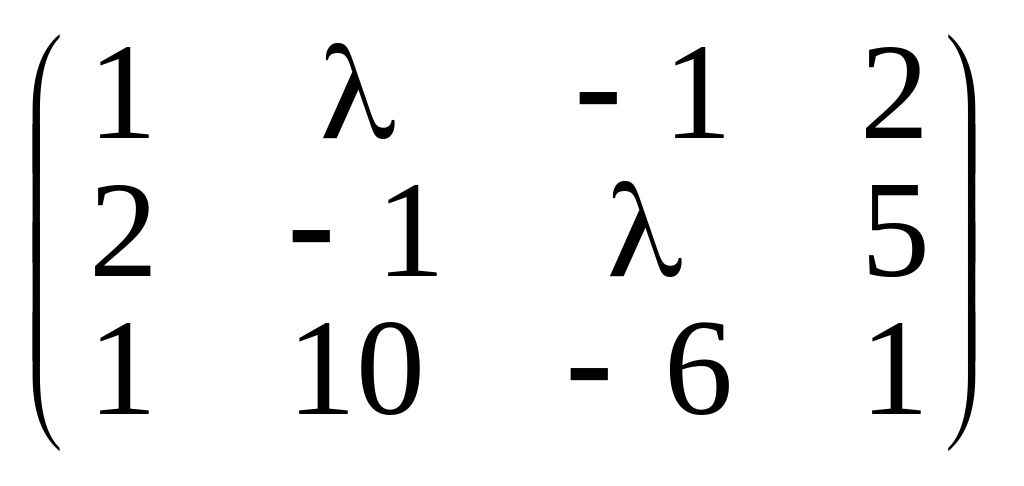 .
.
Відповідь.
а) якщо
![]() ;
якщо
;
якщо
![]() ;
б) якщо
;
б) якщо
![]() ;
якщо
;
якщо
![]() .
.
11. Знайти ранг матриць методом елементарних перетворень:
а)
 ;
б)
;
б)
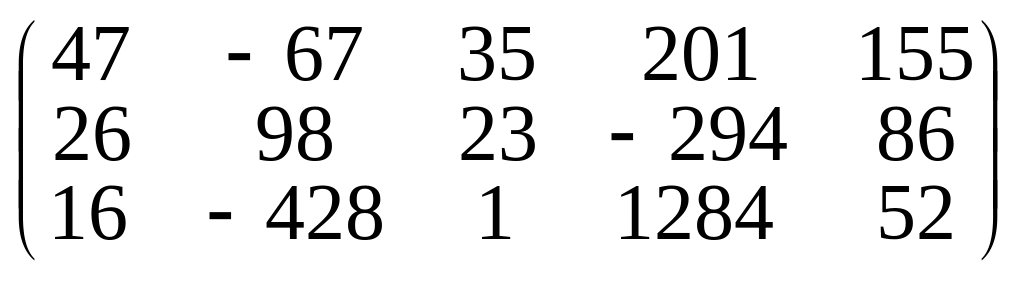 .
.
Відповідь. а) 3; б) 2.
12. Довести, що в результаті приєднання до матриці одного стовпця або рядка її ранг збільшується на одиницю або не змінюється.
Завдання для
самостійної роботи: № 2(б); 4(в); 5(в); 6(в);
7(г)
Практичне заняття № 3 Вектори
1. Лінійні операції з векторами.
2. Застосування скалярного, векторного і мішаного добутків векторів для розв’язування задач. Термінологічний словник ключових понять
Вектор — напрямлений відрізок.
Модуль вектора — довжина вектора.
Напрямні косинуси — косинуси кутів, що утворює вектор з осями координат.
Навчальні завдання
1. Дано три точки А (1, 1, 1), В (2, 2, 1) і С (2, 1, 2). Знайти кут = ВАС.
Знайдемо вектори
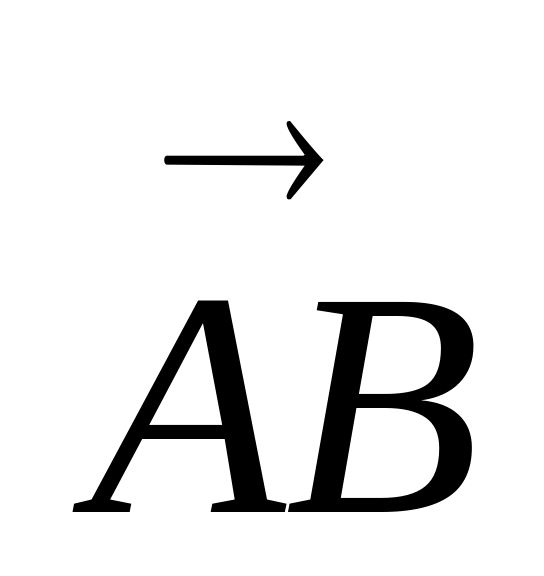 =
(1, 1, 0),
=
(1, 1, 0),
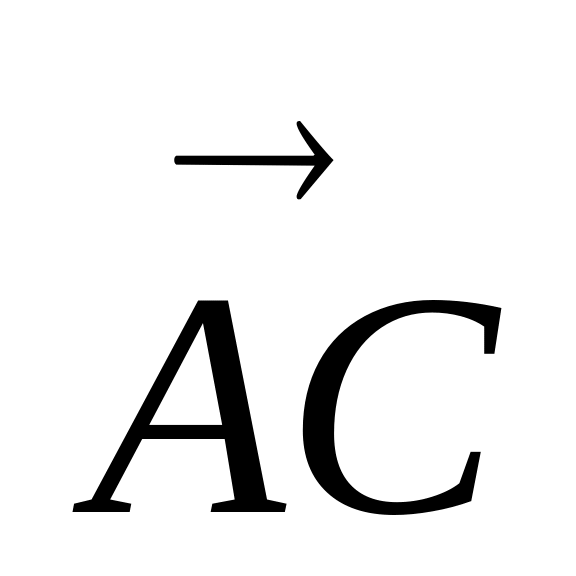 =
(1, 0, 1). Згідно з формулою (2.5) маємо:
=
(1, 0, 1). Згідно з формулою (2.5) маємо:
![]() ,
отже, = 60.
,
отже, = 60.
2. Знайти
площу паралелограма, побудованого на
векторах
![]() =
(5,
2, 7),
=
(5,
2, 7),
![]() =
(1, 2, 4) як на сторонах.
=
(1, 2, 4) як на сторонах.
Знайдемо векторний добуток векторів і :
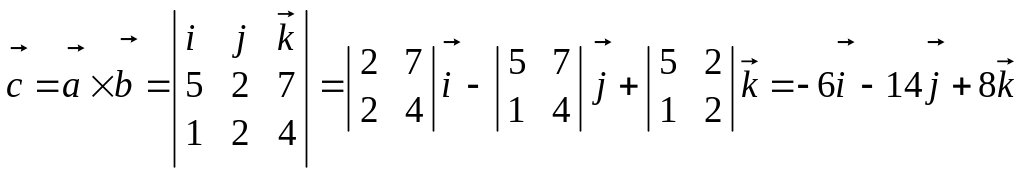 .
.
Знайдемо
![]() кв. од.
кв. од.
3. У просторі задано чотири точки А (1, 1, 1), В (4, 4, 4), С (3, 5, 5), D (2, 4, 7). Знайти об’єм піраміди АВСD.
З елементарної математики відомо, що об’єм піраміди АВСD дорівнює одній шостій об’єму паралелепіпеда, побудованого на векторах
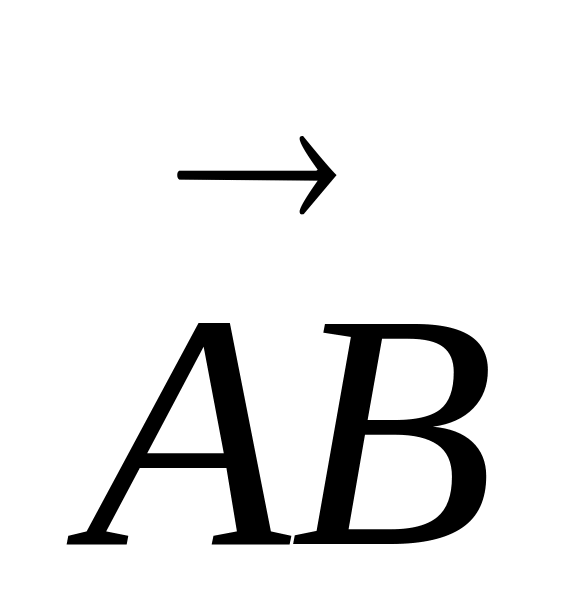 ,
,
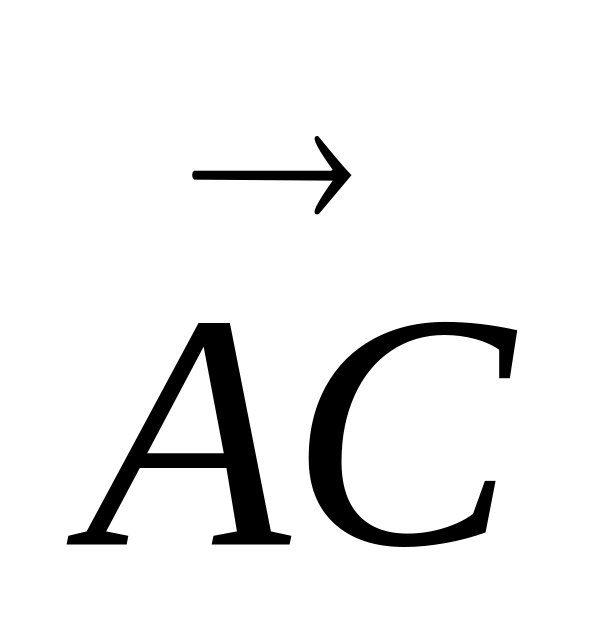 і
і
 ,
а останній, у свою чергу, дорівнює модулю
мішаного добутку. Отже, маємо:
,
а останній, у свою чергу, дорівнює модулю
мішаного добутку. Отже, маємо:
= (3, 3, 3), = (2, 4, 4), = (1, 3, 6);
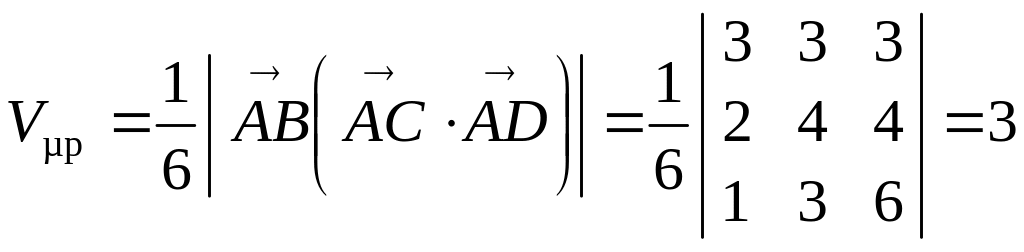 куб. од.
куб. од.
4. Дано трикутник А (4, 1), В (7, 5), С (– 4, 7). Знайти площу трикутника, вершини якого містяться в точках перетину бісектрис трикутника зі сторонами (рис. 2.13).
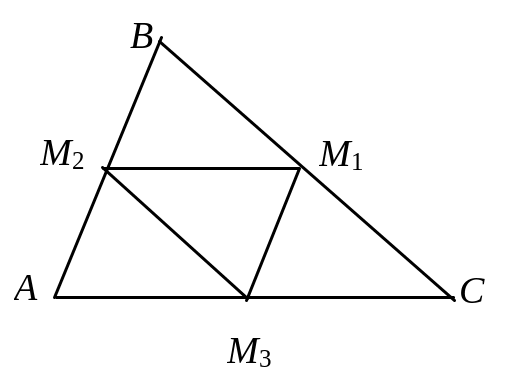
Рис. 2.13
Бісектриса трикутника поділяє протилежну сторону на відрізки, пропорційні прилеглим сторонам. Знайдемо довжину відрізків АВ, ВС і АС за формулами (2.10).
![]() ,
,
![]() ,
,
![]() .
.
Знайдемо відношення, в яких основи бісектрис точки М1, М2, М3 (рис. 2.13) поділяють відповідні відрізки:
![]() .
.
Скориставшись формулами (2.11) і (2.12), знайдемо відповідно координати точок М1 (х1, у1), М2 (х2, у2), М3 (х3, у3).
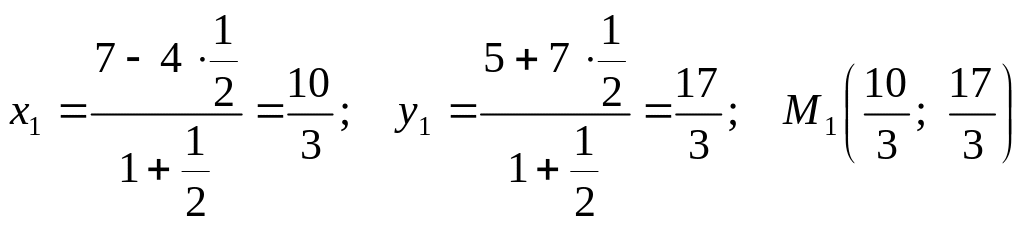 ;
;
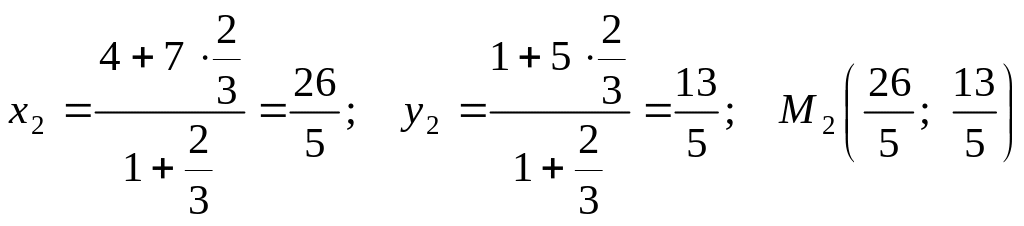 ;
;
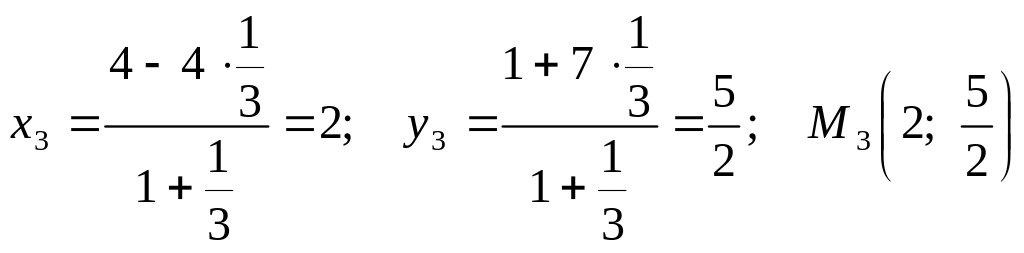 .
.
Площу трикутника М1 М2 М3 обчислимо за формулою (2.13):
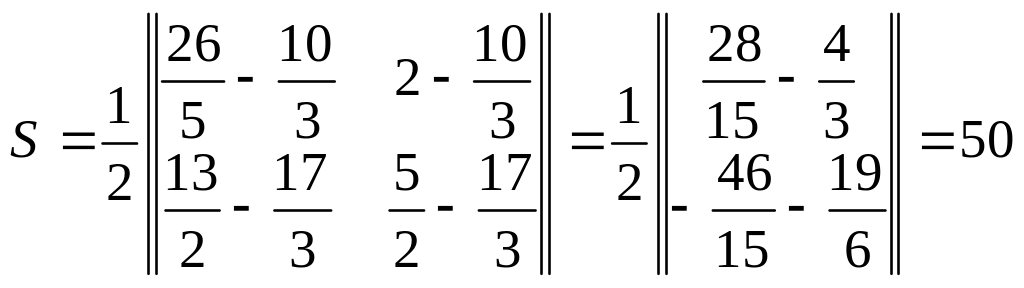 кв. од.
кв. од.
