Методичні вказівки до проведення практичних робіт

Практичне заняття – форма навчального заняття, при якій викладач організує детальний розгляд студентами окремих теоретичних положень навчальної дисципліни та формує вміння і навички їх практичного застосування шляхом індивідуального виконання студентом відповідно сформульованих завдань.

Практичні заняття проводяться в аудиторіях або в навчальних лабораторіях, оснащених необхідними технічними засобами навчання, обчислювальною технікою. Практичне заняття проводиться з студентами, кількість яких не перевищує половини академічної групи.

Перелік тем практичних занять визначається робочою навчальною програмою дисципліни. Проведення практичного заняття ґрунтується на попередньо підготовленому методичному матеріалі - тестах для виявлення ступеня оволодіння студентами необхідними теоретичними положеннями, наборі завдань різної складності для розв'язування їх студентами на занятті.

Вказані методичні засоби готуються викладачем, якому доручено проведення практичних занять, за погодженням з лектором даної навчальної дисципліни. Практичне заняття включає проведення попереднього контролю знань, умінь і навичок студентів, постановку загальної проблеми викладачем та її обговорення за участю студентів, розв'язування завдань з їх обговоренням, розв'язування контрольних завдань, їх перевірку, оцінювання.

Оцінки, отримані студентом за окремі практичні заняття, враховуються при виставленні підсумкової оцінки з даної навчальної дисципліни. Поточний контроль виконання практичних робіт здійснюється під час проведення практичних занять і має своєю метою перевірку рівня підготовленості студента. Об'єктами такого контролю є:

– підготовка студента до практичної роботи, якість ведення журналу відвідування занять;

– виконання безпосередньо практичних завдань;

– захист практичної роботи, який включає відповіді на контрольні запитання, що наведені в практичних роботах.

Оцінювання знань, вмінь та навичок студентів враховує види занять, які згідно з програмою дисципліни «Вища математика» передбачають практичні заняття та самостійну роботу у таких формах:

– контроль виконання практичних робіт;

– контроль завдань для самостійної роботи;

– контроль виконання контрольної роботи.

Практичне заняття № 1 Обчислення визначників План

1. Обчислення визначників третього порядку.

2. Обчислення визначників n-го порядку.

3. Розв’язування систем n рівнянь з n невідомими за правилом Крамера.

Термінологічний словник ключових понять

Транспонування — зміна місцями рядків і стовпців визначника або матриці.

Мінор k-го порядку — визначник, утворений з елементів визначника або матриці, розміщених на перетині k рядків і k стовпців.

Навчальні завдання

Алгебраїчне доповнення до мінора — визначник, що складається з елементів, котрі не належать тим рядкам і тим стовпцям визначника, з яких утворено мінор, і береться зі знаком , де i₁ i₂, ..., i_k, j₁, j₂, ..., j_k, — індекси відповідно тих рядків і тих стовпців, які брали участь в утворенні мінора.

1. Обчислити визначник за правилом трикутників.

.

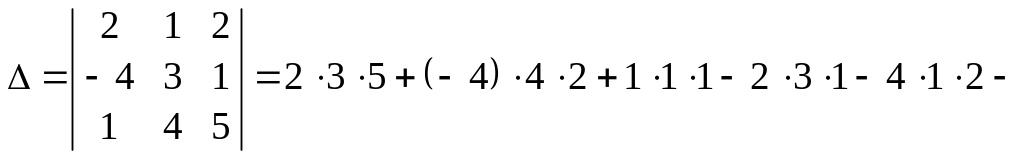
2. Обчислити визначник за правилом Саррюса.

.

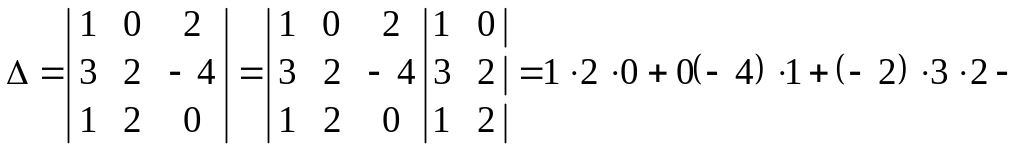
3. Утворити доповняльний мінор другого порядку.

Для визначника ∆ запишемо мінор другого порядку:

; .

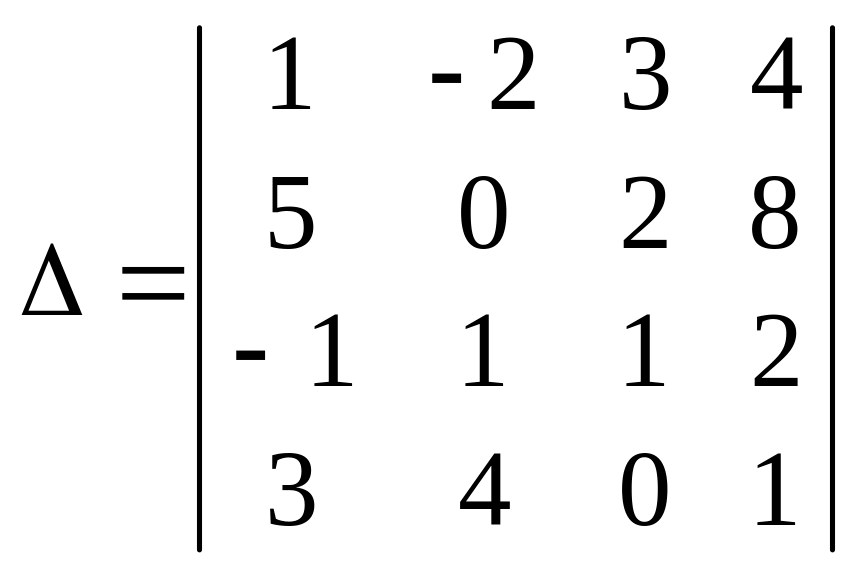Цей мінор утворено з елементів, які містяться на перетині пер­шого і третього рядків та другого і четвертого стовпців. Викреслимо ці рядки та стовпці з визначника дістанемо — мінор, доповняльний до мінора другого порядку :

.

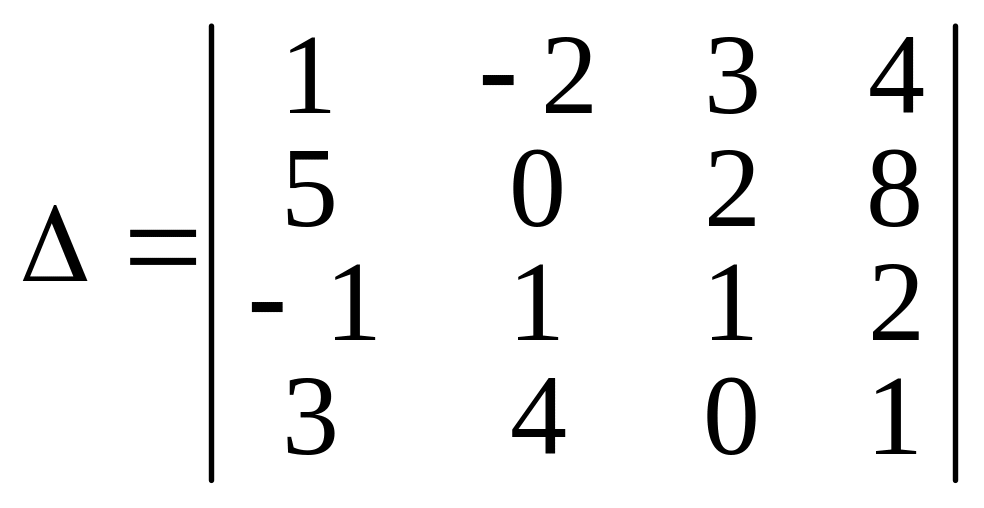
4. Обчислити визначник

.

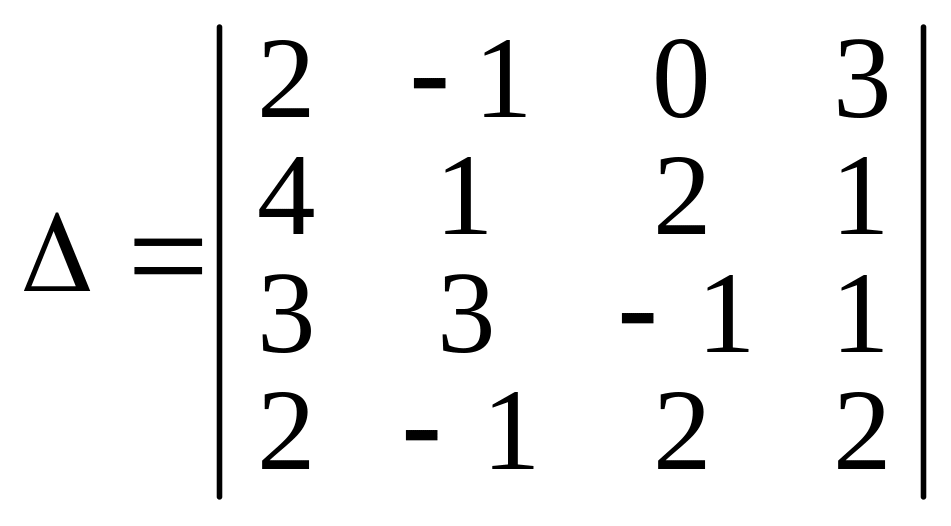 Скориставшись означенням визначника, утворимо алгебраїч­ну суму добутків елементів, наприклад першого рядка, на їх алгебраїчні доповнення:

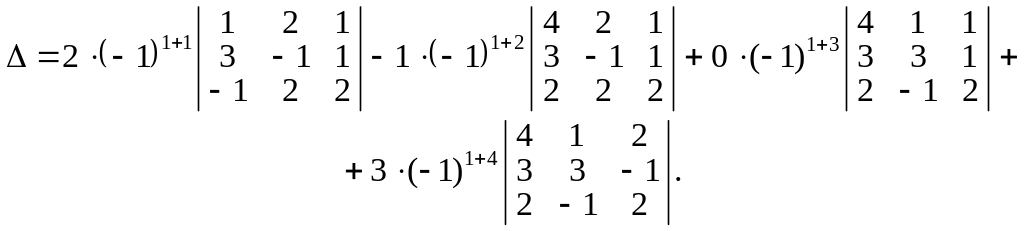
Отже, тепер потрібно обчислити три визначники третього порядку, оскільки визначник, який входить до третього доданка, обчислювати не потрібно. Зрозуміло, що чим більше нулів маємо в рядку або стовпці, за елементами якого утворюється алгебраїчна сума, тим менше визначників (n–1)-го порядку потрібно обчислювати.

Згідно з властивістю 8 утворимо в одному зі стовпців визначника , наприклад в останньому, нулі. Якщо нулі утворюються в стовпці, використовуються елементи рядків, а якщо нулі утворюються в рядках, то навпаки — елементи стовпців. У четвертому стовпці є дві одиниці, одну з них візьмемо як розв’язувальний елемент і на підставі властивості 8 виконаємо перетворення:

1. елементи третього (робочого) рядка перепишемо у перетворюваний визначник без змін;

2. помножимо всі елементи третього рядка на –3, додамо до відповідних елементів першого рядка, а результат запишемо в перший рядок;

3. помножимо всі елементи третього рядка на –1, додамо до відповідних елементів другого рядка, а результат запишемо у другий рядок;

4. помножимо всі елементи третього рядка на –2, додамо до відповідних елементів четвертого рядка, а результат запишемо в четвертий рядок.

Після цих перетворень значення визначника не зміниться, але він набере такого вигляду:

.

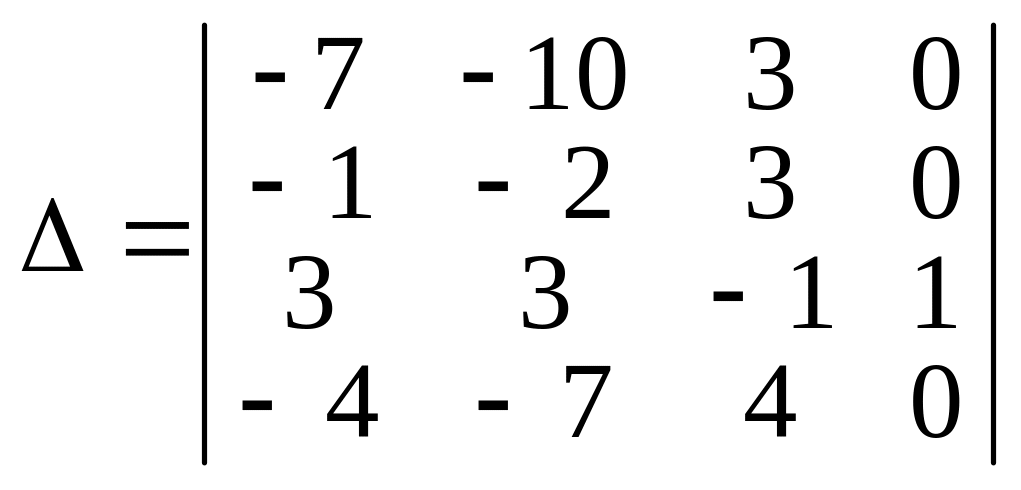Тепер, скориставшись означенням визначника і розклавши його за елементами четвертого стовпця, дістанемо:

.

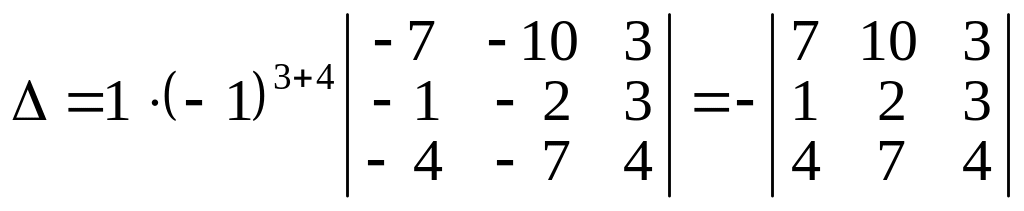Останній визначник записано згідно з властивістю 5, і тепер обчислення визначника четвертого порядку звелось до обчислення одного визначника третього порядку. Його можна обчислити за означенням, а можна знову утворити нулі, скажімо, у другому рядку, скориставшись одиницею як розв’язувальним елементом і виконавши дії згідно з властивістю 8 зі стовпцями. Дістанемо:

.

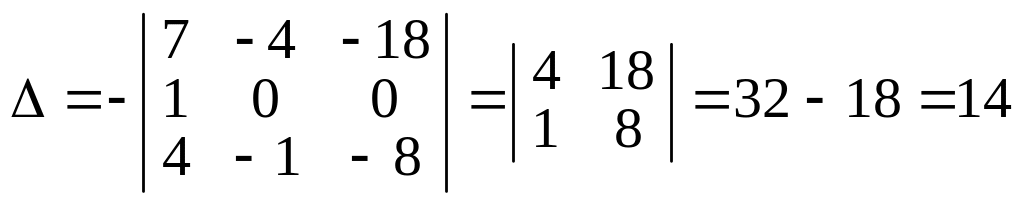Зрозуміло, що за такою схемою можна обчислити визначник будь-якого порядку.

5. Розв’язати систему рівнянь:

 Складемо й обчислимо спочатку головний визначник цієї системи: 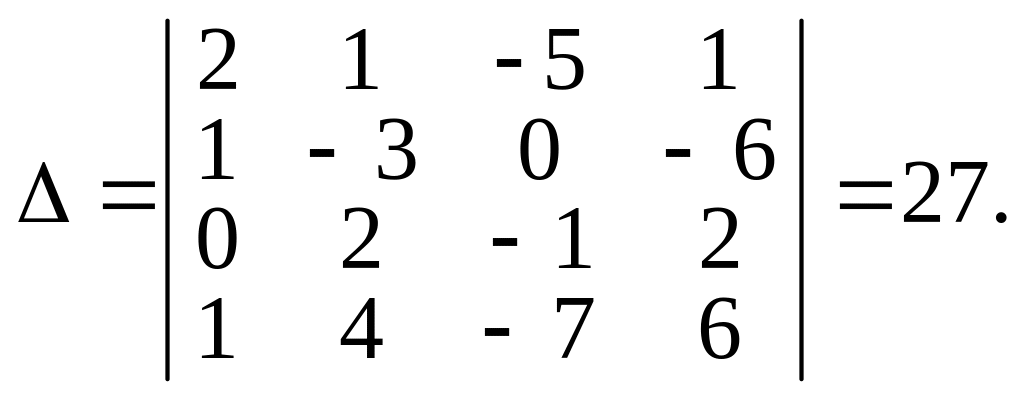Отже, головний визначник системи рівнянь відмінний від нуля. За правилом Крамера така система має єдиний розв’язок. Знайдемо його. Для цього утворимо і обчислимо ще чотири визначники:

За правилом Крамера маємо розв’язки:

Отже, , — єдиний розв’язок.