8. Полосовые фильтры

Полосовой фильтр представляет собой устройство, которое пропускает сигналы в диапазоне частот с шириной полосы BW, расположенной приблизительно вокруг центральной частоты f_o (Гц) или _o=2πf_o (рад/с). На рис. 6 изображены идеальная и реальная амплитудно-частотные характеристики. В реальной характеристике частоты _L и _U представляют собой нижнюю и верхнюю частоты среза и определяют полосу пропускания _L≤≤_U и ее ширину BW=_U.- _L

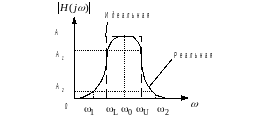
Рис. 6. Идеальная и реальная амплитудно-частотные характеристики полосового фильтра.

В полосе пропускания амплитудно-частотная характеристика никогда не превышает некоторого определенного значения, например А₁ на рис. 6. Существует также две полосы задерживания 0≤≤₁ и ≥₂, где значение амплитудно-частотной характеристики никогда не превышает заранее выбранного значения, скажем A₂. Диапазоны частот между полосами задерживания и полосой пропускания, а именно ₁<<_L и _U<<₂, образуют соответственно нижнюю и верхнюю переходные области, в которых характеристика является монотонной.

Передаточные функции полосовых фильтров можно получить из нормированных функций нижних частот переменной s с помощью преобразования

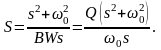(1)

Отношение Q=_o/BW характеризует качество самого фильтра и является мерой его избирательности. Высокому значению Q соответствует относительно узкая, а низкому значению Q — относительно широкая ширина полосы пропускания. Коэффициент усиления фильтра К определяется как значение его амплитудно-частотной характеристики на центральной частоте; таким образом K=│H(j_o)│.

В каждом случае центральная частота и частота среза связаны следующим соотношением:

,

где

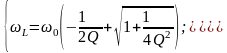(2)

Путем последовательного соединения ФНЧ и ФВЧ получаются полосовые фильтры с широкой полосой пропускания. При этом частота среза фильтра нижних частот должна быть выше частоты среза верхних частот и лишь в частном случае эти частоты могут быть взяты равными.

9. Фильтры Чебышева

Как было отмечено выше, фильтр Чебышева представляет собой оптимальный полиномиальный фильтр. Его а.ч.х. определяется следующим выражением :

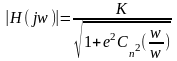, (1)

где n = 1, 2, 3,...

Параметры  и К постоянные числа, а С_n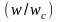 - полином Чебышева первого рода степени n, который имеет вид :

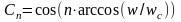при 0   1 , (2)

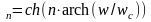при  1

А.ч.х. достигает своего наибольшего значения , равного К в тех точках, в которых С_n = 0. Поскольку эти точки распределены в полосе пропускания, то характеристика фильтра Чебышева содержит пульсации в полосе пропускания и монотонна в полосе задержания. Размах этих пульсаций определяет параметр , а их число - порядок фильтра n. Коэффициент усиления фильтра Чебышева определяется значением К. На рис. 10 представлены характеристики фильтров Чебышева различных порядков для K=1.

/H(j)/

1

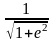
0,5

0

0

0,5

1

1,5

 /_c

Характеристика идеального ФНЧ

n=2

n=4

n=6

R_

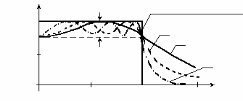
Рис.7. А.ч.х. нормированных фильтров нижних частот Чебышева

различных порядков.

Фильтр Чебышева часто называют равноволновым фильтром. Для К=1 размах пульсаций R_ составляет :

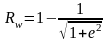. (3)

Размах пульсаций, или неравномерность в полосе пропускания выражается в децибелах (дБ) следующим образом :

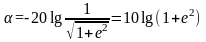. (4)

Значение  используют как характеристику фильтра Чебышева. Например, фильтр с неравномерностью передачи 0,5 дБ обладает таким значением , при котором  = 0,5. Или, разрешая (4) относительно , можно найти :

.

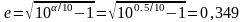Наибольшим размахом пульсаций обладает фильтр Чебышева с неравномерностью передачи 3 дБ, для которого  =1.