
1.2 Истечение жидкости из отверстия
Рассмотрим истечение идеальной несжимаемой жидкости из небольшого отверстия в широком открытом сосуде (рис. 3). Выделим мысленно в жидкости трубку тока, сечениями которой являются открытая поверхность жидкости S1 и сечение струи при выходе из отверстия S2 (если не принять специальных мер, то сечение струи будет меньше отверстия). Для всех точек каждого из этих сечений скорость жидкости v и высоту h над некоторым исходным уровнем можно считать одинаковыми. Поэтому к данным сечениям можно применить теорему Бернулли. Давления р1 и р2 в обоих сечениях одинаковы и равны атмосферному. Скоростью v1 перемещения открытой поверхности жидкости ввиду ее малости можно пренебречь. Поэтому уравнение в данном случае упрощается следующим образом:

Рисунок
3. Истечение
идеальной несжимаемой жидкости из
небольшого отверстия в широком открытом
сосуде
ρgh1 = pʋ2\2 + ρgh2 (8)
 где
v
— скорость жидкости в сечении S2
(скорость истечения из отверстия).
Сократив на р, можно написать, что
где h
= h1
— h2
— высота открытой поверхности над
отверстием.
где
v
— скорость жидкости в сечении S2
(скорость истечения из отверстия).
Сократив на р, можно написать, что
где h
= h1
— h2
— высота открытой поверхности над
отверстием.
 (9)
(9)
Формула называется формулой Торричелли. Из нее следует, что скорость истечения жидкости из отверстия, находящегося на глубине h под открытой поверхностью жидкости, совпадет со скоростью, которую приобретает любое тело, падая с высоты h (в случае, если сопротивлением воздуха можно пренебречь). Этот результат получен в предположении, что жидкость идеальна. Для реальных жидкостей скорость истечения будет меньше, причем тем сильнее отличается от значения, определяемого формулой Торричелли, чем больше внутреннее трение в жидкости. Например, глицерин будет вытекать из сосуда медленнее, чем вода.
Если сечение потока жидкости достаточно велико, то уравнение Бернулли следует применять к линиям тока, то есть линиям, вдоль которых перемещаются частицы жидкости при стационарном течении. Например, при истечении идеальной несжимаемой жидкости из отверстия в боковой стенке или дне широкого сосуда линии тока начинаются вблизи свободной поверхности жидкости и проходят через отверстие (рисунок. 4).
|
Рисунок 4 Истечение жидкости из широкого сосуда. |
Поскольку скорость жидкости вблизи поверхности в широком сосуде пренебрежимо мала, то уравнение Бернулли принимает вид:
|
 где
p – атмосферное давление, h – перепад
высоты вдоль линии тока. Таким образом,
где
p – атмосферное давление, h – перепад
высоты вдоль линии тока. Таким образом,
(11)
|
Это выражение для скорости истечения называют формулой Торричелли. Скорость истечения идеальной жидкости из отверстия в сосуде такая же, как и при свободном падении тела с высоты h без начальной скорости. В отличие от жидкостей, газы могут сильно изменять свой объем. Расчеты показывают, что сжимаемостью газов можно пренебречь, если наибольшие скорости в потоке малы по сравнению со скоростью звука в этом газе. Таким образом, уравнение Бернулли можно применять к достаточно широкому классу задач аэродинамики. Одной из таких задач является изучение сил, действующих на крыло самолета.
 Строгое
теоретическое решение этой задачи
чрезвычайно сложно, и обычно для
исследования сил применяются
экспериментальные методы. Уравнение
Бернулли позволяет дать лишь качественное
объяснение возникновению подъемной
силы крыла.
На рисунке 4 изображены линии тока
воздуха при обтекании крыла самолета.
Из-за специального профиля крыла и
наличия угла
атаки,
то есть угла наклона крыла по отношению
к набегающему потоку воздуха, скорость
воздушного потока над крылом оказывается
больше, чем под крылом. Поэтому на рис.4
линии тока над крылом располагаются
ближе друг к другу, чем под крылом. Из
уравнения Бернулли следует, что давление
в нижней части крыла будет больше, чем
в верхней; в результате появляется
сила
Строгое
теоретическое решение этой задачи
чрезвычайно сложно, и обычно для
исследования сил применяются
экспериментальные методы. Уравнение
Бернулли позволяет дать лишь качественное
объяснение возникновению подъемной
силы крыла.
На рисунке 4 изображены линии тока
воздуха при обтекании крыла самолета.
Из-за специального профиля крыла и
наличия угла
атаки,
то есть угла наклона крыла по отношению
к набегающему потоку воздуха, скорость
воздушного потока над крылом оказывается
больше, чем под крылом. Поэтому на рис.4
линии тока над крылом располагаются
ближе друг к другу, чем под крылом. Из
уравнения Бернулли следует, что давление
в нижней части крыла будет больше, чем
в верхней; в результате появляется
сила ![]() действующая
на крыло. Вертикальная составляющая
действующая
на крыло. Вертикальная составляющая ![]() этой
силы называется подъемной силой.
Подъемная сила позволяет скомпенсировать
силу тяжести, действующую на самолет,
и тем самым она обеспечивает возможность
полета тяжелых летательных аппаратов
в воздухе. Горизонтальная
составляющая
этой
силы называется подъемной силой.
Подъемная сила позволяет скомпенсировать
силу тяжести, действующую на самолет,
и тем самым она обеспечивает возможность
полета тяжелых летательных аппаратов
в воздухе. Горизонтальная
составляющая ![]() представляет
собой силу сопротивления среды.
представляет
собой силу сопротивления среды.


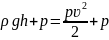 (10)
(10)