4.2 Содержание типового расчета

Исследовать функцию двух переменных на экстремум:  z = Ax³ + Bx²y + Cxy²+ Dy³ + Ex+ Fy + G.

4.3 Пример выполнения типового расчета

Исследовать на экстремум функцию  z = – 5x³ – 4x²y + xy² – 3y³ + 27x + 36y + 4.  Решение.   Найдём частные производные первого порядка  z_x' (x, y) = – 15x² – 8xy + y² + 27;     z_y' (x, y) = – 4x² + 2xy – 9y² + 36.  Для нахождения стационарных точек нужно решить систему уравнений 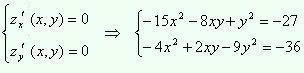   Левые части уравнений системы являются однородными многочленами второго порядка относительно x и y(каждое слагаемое имеет второй порядок относительно x и y). Чтобы решить систему умножим каждое из уравнений на такое число, чтобы при сложении уравнений друг с другом свободный член обращался в нуль. Для этого первое уравнение умножим на – 4, а второе на 3. 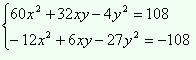   Складывая уравнения, получим  48x² + 38xy – 31y² = 0.  Замечаем, что y = 0 не является решением исходной системы уравнений, поэтому можно обе части полученного уравнения поделить на y² и ввести новое переменное     48t² + 38t – 31 = 0.  Полученное квадратное уравнение имеет корни  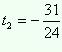  .  1) Пусть   или  ,   y = 2x.   Подставим в первое уравнение системы, получим  –15x² – 16x² + 4x² = –27;       –27x² = –27;       x² = 1;       x = ±1.  Получили две точки  M₁(1; 2) и M₂(–1; –2).  2) Теперь рассмотрим 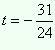   или 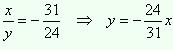 .  Снова подставляем в первое уравнение системы :    Умножим обе части уравнения на 31² и вынесем в левой части уравнения x² за скобки  (–15 · 31² + 8 · 24 · 31 + 24² ) x² = –27 · 31²  Проведя расчёт, получим –7887x² = –25947,   x² ≈ 3,29,   x ≈ ±1,81.  Учитывая, что   получаем ещё две стационарные точки M₃(1,81; –1,40),  M₄(–1,81; 1,40).  Найдём частные производные второго порядка            Определим знак   Δ = AC – B²   в каждой из стационарных точек  1) Точка   M₁(1; 2).  A = (–30x – 8y)|_M1 = – 46;     C = (2x – 18y)|_M1 = – 34;  B = (–8x + 2y)|_M1 = – 4;     Δ = (– 46)·(–34) – (– 4)² = 1548 > 0.  Так как Δ > 0, то в точке M₁ существует экстремум. Поскольку A = – 46 < 0, то M₁(1; 2) - точка максимума.  2) Точка   M₂(–1; –2).  A = (–30x – 8y)|_M2 = 46;     C = (2x – 18y)|_M2 = 34;  B = (–8x + 2y)|_M2 = 4;     Δ = 46·34 – 4² = 1548 > 0.  В точке M₂ также Δ > 0, т.е. существует экстремум. Однако здесь A = 46 > 0, поэтому M₂(–1; –2) - точка минимума.  3) Точка   M₃(1,81; –1,40).  A = (–30x – 8y)|_M3 = – 43,1;     C = (2x – 18y)|_M3 = 28,82;  B = (–8x + 2y)|_M3 = 17,28;     Δ = – 43,1·28,82 – 17,28² < 0.  Так как Δ < 0, то в точке M₃ экстремума нет.  4) Точка   M₄(–1,81; 1,40).  A = (–30x – 8y)|_M4 = 43,1;     C = (2x – 18y)|_M4 = – 28,82;  B = (–8x + 2y)|_M4 = – 17,28;     Δ = 43,1·(–28,82) – (–17,28)² < 0.  Экстремума в точке M₄ нет.  Вычислим значения исследуемой функции в точках экстремума M₁(1; 2) и M₂(–1; –2)  z_max(M₁) = z_max(1; 2) = 70;  z_min(M₂) = z_min(–1; –2) = – 62.  Ответ:

№	x	y	экстремум	z
1	1	2	максимум	70
2	–1	–2	минимум	–62
3	1,81	–1,40	экстремума нет	–
4	–1,81	1,40	экстремума нет	–

4.4 Оформление отчета

В отчете необходимо привести все проделанные выкладки. В ответе записать координаты всех найденных критических точек. Для каждой точки записать результат проведенного исследования: есть ли там экстремум или нет, если есть, то какой – максимум или минимум. Если в критической точке существует экстремум, необходимо вычислить значение функции в этой точке. Результаты исследования свести в таблицу, как показано в примере. В ответе все расчетные величины записать в десят5.3 Приложения двойных интегралов

Плоская область D ограничена линиями, указанными в условии задачи.  Г(x,y) - поверхностная плотность области D.  Для этой области требуется найти:  1. S - площадь;  2. M - массу;  3. M_y, M_x - статические моменты относительно осей Oy и Ox соответственно;  4. x_c, y_c - координаты центра масс.

Типовой расчет состоит из двух задач.

Задача 1. Границы области D: y = x 2 − x ,    y = x  Поверхностная плотность этой области задана функцией Γ ( x , y ) = 7 

Задача 2. Границы области D: x 2 + y 2 = 5 ⁢ x ,     x 2 + y 2 = 3 ⁢ x ,     y = − x ,     ( y ≥ − x )  Поверхностная плотность этой области задана функцией Γ ( x , y ) = 7 ⁢ x 2 + y 2 

4. ичных дробях с тремя значащими цифрами.