
- •3.1 Нахождение наибольшего и наименьшего значения функции нескольких переменных в замкнутой области
- •3.1 Нахождение наибольшего и наименьшего значения функции в замкнутой области
- •Порядок выполнения работы:
- •Литература
- •1 Hахождение наибольшего и наименьшего значения функции нескольких переменных в замкнутой области
- •1.1 Теоретическое введение
- •1.2 Содержание типового расчета
- •1.3 Пример выполнения типового расчета
- •1.4 Оформление отчета
- •3.3 Функции нескольких переменных, приложения градиента
- •3 Функции нескольких переменных. Приложения градиента
- •3.1 Теоретическое введение
- •3.1.1 Производная по направлению и градиент
- •3.2 Содержание типового расчета
- •3.3 Пример выполнения типового расчета
- •3.4 Оформление отчета
- •3.3 Применение градиента Порядок выполнения работы:
- •4.2 Содержание типового расчета
- •4.3 Пример выполнения типового расчета
- •3 Приложения двойных интегралов
- •3.1 Теоретическое введение
- •3.1.1 Вычисление площади и массы плоской пластины
- •3.1.2 Статические моменты. Центр масс плоской пластины
- •3.2 Содержание типового расчета
- •3.3 Порядок выполнения типового расчета
- •3.4 Примеры выполнения типового расчета
- •3.5 Оформление отчета в отчете должны быть представлены все выполненные расчеты, аккуратно выполненные чертежи. Численные ответы должны быть получен5.4 Приложения тройных интегралов
- •4 Приложения тройных интегралов
- •4.1 Теоретическое введение
- •4.1.1 Вычисление площади и массы пространственного тела
- •4.1.2 Статические моменты. Центр масс пространственного тела
- •4.1.3 Момент инерции пространственного тела
- •4.2 Содержание типового расчета
- •4.3 Порядок выполнения типового расчета
- •4.4 Пример выполнения типового расчета
- •4.5 Оформление отчета
3.3 Применение градиента Порядок выполнения работы:
Задача 1 1. Найти градиент функции U(X, Y) в точке M. 2. Найти вектор E, задающий направление. 3. Вычислить производную функции U(X, Y) по направлению вектора E как проекцию градиента U в точке M на направление вектора E.
Задача 2 1. Найти вектор N(X, Y, Z) нормали к поверхности S в произвольной точке M(X, Y, Z). 2. Найти вектор N1 нормали к плоскости P. 3. Найти точку M0(X0, Y0, Z0) на поверхности S, касательная плоскость в которой параллельна плоскости P, используя условие коллинеарности векторов N и N1. 4. Написать уравнение искомой плоскости. Если задача имеет более одного решения, в ответе написать уравнения всех плоскостей, удовлетворяющих данному условию.
Литература
Пискунов Н.С. Дифференциальное и интегральное исчисления. Т.1- М.: Наука, 1978, стр. 273-3.4 Нахождение экстремумов функции двух переменных
Найти экстремумы функции двух переменных
f ( x , y ) = − x 3 − 2 x 2 y + 3 x y 2 − 2 y 3 + 61 x + 14 y − 3
278. 4 Hахождение экстремумов функции двух переменных
4.1 Теоретическое введение
Пусть функция двух переменных z = f (x, y) = f (P) непрерывна в некоторой области G. Функция двух переменных имеет в точке P0 (x0, y0) области G максимум, если существует такая окрестность этой точки, что для всех точек P(x, y) этой окрестности, отличных от P0, выполняется неравенство f (P0) > f (P). Точка P0 называется при этом точкой максимума функции f (x, y). Функция двух переменных имеет в точке P0 (x0, y0) области G минимум, если существует такая окрестность этой точки, что для всех точек P(x, y) этой окрестности, отличных от P0, выполняется неравенство f (P0) < f (P). При этом точка P0 называется точкой минимума функции f (x, y). Существует общее название для максимума и минимума – экстремум. Необходимое условие существования экстремума. Если в точке P0 (x0, y0) функция z = f (x, y) имеет экстремум и если в этой точке существуют частные производные первого порядка от функции z = f (x, y), то эти производные равны нулю, т.е.
fx' (x0, y0) = 0; fy' (x0, y0) = 0 |
(1) |
Точки, в которых частные производные первого порядка функции z = f (x, y) равны нулю, называютсястационарными. Точки, в которых частные производные первого порядка обращаются в нуль или не существуют, называются критическими этой функции. Точки экстремума функции следует искать среди её критических точек. Однако существуют критические точки, не являющиеся точками экстремума. Достаточное условие существования экстремума. Пусть точка P0(x0, y0) является стационарной для функцииz = f (x, y) и пусть в этой точке существуют и непрерывны все частные производные второго порядка. Обозначим
A = |
(2) |
и определитель второго порядка
Δ = |
(3) |
Если Δ > 0, то функция f (x, y) имеет в точке P0 экстремум: минимум при A > 0 и максимум при A < 0. Если Δ < 0, то в точке P0 функция f (x, y) экстремума не имеет. Если Δ = 0, то для заключения о характере стационарной точки требуется дополнительное исследование.
Пример.
Исследовать на экстремум функцию
z = x3 + y3 –
3x –
12y +
8.
Решение.
Найдём частные производные первого
порядка
zx'
(x, y)
= 3x2 –
3, zy'
(x, y)
= 3y2 –
12.
Найдём
стационарные точки, решая систему
уравнений (1)
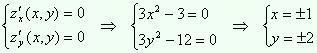 .
Заданная
функция имеет четыре стационарные
точки
M1 (1;
2), M2 (–1;
–2), M3 (1;
–2), M4 (–1;
2).
Найдём
частные производные второго порядка
(2)
.
Заданная
функция имеет четыре стационарные
точки
M1 (1;
2), M2 (–1;
–2), M3 (1;
–2), M4 (–1;
2).
Найдём
частные производные второго порядка
(2)
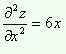 ,
,
 ,
,
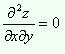 .
Определим
знак Δ = AC – B2
в каждой из стационарных точек
1)
Точка M1 (1;
2) :
A =
6x|x=1 =
6, C =
6y|y=2 =
12, B =
0, Δ = 6 · 12 – 0 = 72 > 0.
Так
как Δ > 0, то в точке M1 существует
экстремум. Поскольку A =
6 > 0, то M1(1;
2) – точка минимума.
2)
Точка M2 (–1;
–2) :
A =
6x|x=
–1 =
– 6, C =
6y|y=-2 =
–12, B =
0, Δ = (– 6) · (–12) = 72 > 0.
В
точке M2 также
Δ > 0, т.е. существует экстремум. Однако
здесь A =
– 6 < 0, поэтому M2(–1;
–2) – точка максимума.
3)
Точка M3 (1;
–2) :
A =
6x|x=1 =
6, C =
6y | y=
–2 =
–12, B =
0, Δ = 6 · (–12) – 0 = –72 < 0.
Так
как Δ < 0, то в точке M3 экстремума
нет.
4)
Точка M4 (–1;
2) :
A =
6x|x =
–1 =
– 6, C =
6y|y =
2 =
12, B =
0, Δ = – 6 · 12 – 0 = –72 < 0.
Экстремума
в точке M4 нет.
Теперь
вычислим значения заданной функции в
точках экстремума M1(1;
2) и M2(–1;
–2) .
zmax(M2)
= zmax(–1;
–2) = (–1)3 +
(–2)3 –
3·(–1) – 12·(–2) + 8 = 24.
zmin(M1)
= zmin(1;
2) = 13 +
23 –
3 · 1 – 12 · 2 + 8 = –10.
Ответ: zmax(M2)
= zmax(–1;
–2) = 24; zmin(M1)
= zmin(1;
2) = –10. В точках M3 (1;
–2) и M4 (–1;
2) экстремумов нет.
.
Определим
знак Δ = AC – B2
в каждой из стационарных точек
1)
Точка M1 (1;
2) :
A =
6x|x=1 =
6, C =
6y|y=2 =
12, B =
0, Δ = 6 · 12 – 0 = 72 > 0.
Так
как Δ > 0, то в точке M1 существует
экстремум. Поскольку A =
6 > 0, то M1(1;
2) – точка минимума.
2)
Точка M2 (–1;
–2) :
A =
6x|x=
–1 =
– 6, C =
6y|y=-2 =
–12, B =
0, Δ = (– 6) · (–12) = 72 > 0.
В
точке M2 также
Δ > 0, т.е. существует экстремум. Однако
здесь A =
– 6 < 0, поэтому M2(–1;
–2) – точка максимума.
3)
Точка M3 (1;
–2) :
A =
6x|x=1 =
6, C =
6y | y=
–2 =
–12, B =
0, Δ = 6 · (–12) – 0 = –72 < 0.
Так
как Δ < 0, то в точке M3 экстремума
нет.
4)
Точка M4 (–1;
2) :
A =
6x|x =
–1 =
– 6, C =
6y|y =
2 =
12, B =
0, Δ = – 6 · 12 – 0 = –72 < 0.
Экстремума
в точке M4 нет.
Теперь
вычислим значения заданной функции в
точках экстремума M1(1;
2) и M2(–1;
–2) .
zmax(M2)
= zmax(–1;
–2) = (–1)3 +
(–2)3 –
3·(–1) – 12·(–2) + 8 = 24.
zmin(M1)
= zmin(1;
2) = 13 +
23 –
3 · 1 – 12 · 2 + 8 = –10.
Ответ: zmax(M2)
= zmax(–1;
–2) = 24; zmin(M1)
= zmin(1;
2) = –10. В точках M3 (1;
–2) и M4 (–1;
2) экстремумов нет.

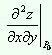 ,
C =
,
C =