3.2 Содержание типового расчета
Задача 1. Задана функция u = f(x, y) и точка M(x0, y0). Найти производную функции u =f(x, y) в точке М в заданном направлении. Установить характер изменения функции в этом направлении.
Задача 2. Для заданной поверхности S найти уравнение касательной плоскости, параллельной заданной плоскости Р.
3.3 Пример выполнения типового расчета
Задача
1.
Найти производную функции u =
3x2 + y2x – y +
2x +
7 в точке M(1;
2) по направлению вектора 
,
если точка N имеет
координаты (– 2; 6). Установить характер
изменения функции в этом направлении.
Решение.
В этом случае скалярное поле – плоское,
т.е. функция поля зависит от двух
переменных: u
= f(x,
y).
Найдем
частные производные функции z в
точке M
;
.
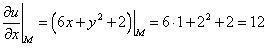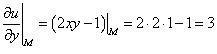Таким
образом grad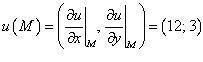 
.
Вектор 
.
.
Затем
находим производную по
направлению:
.
Поскольку 
,
то функция в данном направлении
убывает.
Ответ: grad
u (M)
= (12; 3);
=
– 4,8.
Задача
2. Найти
уравнение касательной плоскости к
эллипсоиду x2 +
10y2 + z2 –
2z =
0, которая параллельна плоскости x –
2y + z –
5 = 0.
Решение. Запишем
уравнение эллипсоида в виде F (x,
y, z)
= x2 +
10y2 + z2 –
2z =
0.
Найдем
градиент функции F (x,
y, z).
Fx′ =
2x;
Fy′ =
20y;
Fz′ =
2z –
2;
grad
F =
(2x,
20y,
2z –
2).
Градиент
функции F (x,
y, z)
в точке касания P0 (x0, y0, z0)
перпендикулярен касательной плоскости.
Следовательно он коллинеарен нормальному
вектору заданной плоскости 
,
т.е. 
(условие
коллинеарности двух векторов).
Запишем
условие коллинеарности через
координаты:
,
откуда
;
;
.
Подставим
полученные выражения для координат
точки касания P0 (x0, y0, z0)
в уравнение эллипсоида :
.
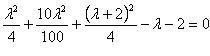Преобразовав
полученное уравнение, получим 
;
.
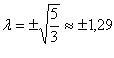Мы
получили два значения для λ,
а следовательно, две точки касания. Это
означает, что существуют две плоскости,
касательные к эллипсоиду и параллельные
заданной плоскости.
Первая
точка касания P1 (x1, y1, z1)
получится при λ1 =
1,29 :
;
;
.
В
качестве нормального вектора к касательной
плоскости возьмем нормаль заданной
плоскости
.
Тогда уравнение касательной плоскости
будет
1(x –
0,645) – 2(y +
0,129) + 1(z –
1,645) = 0,
или
x –
2y + z –
2,548 = 0.
Вторую
точку касания P2 (x2, y2, z2)
найдем при λ2 =
–1,29 :
;
;
.
Аналогично
получим уравнение второй касательной
плоскости
1(x +
0,645) – 2(y –
0,129) + 1(z –
0,355) = 0
или
x –
2 y + z +
0,548 = 0.
В
качестве ответа запишем найденные точки
касания и соответствующие касательные
плоскости:
P1 (0,645;
– 0,129; 1,645), x – 2y + z –
2,548 = 0;
P2 (–
0,645; 0,129; 0,355), x – 2y + z +
0,548 = 0.
3.4 Оформление отчета
В отчете необходимо привести все проделанные выкладки. В ответе записать: - по первой задаче координаты градиента функции и производной по направлению в точке М; - по второй задаче координаты точки касания и уравнение касательной плоскости; если задача имеет два решения, в ответе нужно записать результаты для каждого из решений. В ответе все расчетные величины записать в десятичных дробях с тремя значащими цифрами.