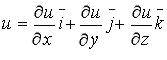1.4 Оформление отчета

2. По каждой задаче необходимо выполнить аккуратный чертеж. На чертеже показать все рассмотренные точки и их координаты. Привести все проделанные выкладки. В ответе указать координаты точек, в которых функция достигает наибольшего и наименьшего значения и величину этих значений.  В ответе все расчетные величины записать в десятичных дробях с тремя значащими цифрами.

3.3 Функции нескольких переменных, приложения градиента

Задача 1. Задана функция  u ⁡ ( x , y ) = e x + y + y ⁢ ( 2 ⁢ x + 1 ) 2    и точка   M ( 1 , 0 ) .  Найти производную функции u(x,y) в точке M в направлении вектора MN, при этом заданы координаты точки N ( 2 , 7 )

Задача 2. Для поверхности S  x 2 + y 2 + z 2 − 6 ⁢ y + 4 ⁢ z = 5  найти уравнение касательной плоскости, параллельной плоскости P 3 ⁢ x + y − 2 ⁢ z − 5 = 0 

Точность расчетов - три значащие цифры. 

3 Функции нескольких переменных. Приложения градиента

3.1 Теоретическое введение

3.1.1 Производная по направлению и градиент

Пусть задана дифференцируемая функция скалярного поля u = F (x, y, z). Рассмотрим точку P (x, y, z) этого поля и луч, выходящий из точки Р в направлении вектора  . Пусть P₁ (x + Δx, y + Δy, z + Δz) – какая-нибудь другая точка этого луча. Разность значений функции u скалярного поля в точках P₁ и Р называется приращением этой функции в направлении   и обозначается Δ_l u.  Δ_l u = F (x + Δx, y + Δy, z + Δz) – F (x, y, z).  Обозначим через Δl расстояние между точками Р и P₁ :­ ­  .  Производной функции u = F (x, y, z) в точке Р по направлению   называется предел 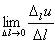 , эта производная обозначается  , т.е.   =  .  Если производная функции u в точке P (x, y, z) по направлению   положительна, то функция u в этом направлении возрастает; если же   < 0, то функция u в направлении   убывает. Производная по направлению дает скорость изменения функции u в этом направлении.  Градиентом в точке P (x, y, z) скалярного поля, заданного дифференцируемой функцией u = F (x, y, z), называется вектор, координаты которого – соответствующие частные производные функции F (x, y, z), вычисленные в точке Р. Градиент обозначается одним из символов grad F (x, y, z), ­ ­ grad F (P),­ ­ grad u.  grad 

или кратко

grad

(1)

Производная функции u = F (x, y, z) по направлению вектора   равна проекции градиента этой функции на вектор  :

u

(2)

3.1.2 Касательная плоскость к поверхности  Пусть поверхность в пространстве задана уравнением

F(x, y, z) = 0,

(3)

левая часть которого является дифференцируемой функцией в некоторой области. Эта функция u = F(x, y, z) определяет скалярное поле, для которого поверхность (3) является одной из поверхностей уровня, т.е. поверхность, на которой функция скалярного поля равна нулю. Пусть в точке P₀(x₀, y₀, z₀) поверхности grad F(x, y, z) не равен нулю. Тогда вектор градиента будет перпендикулярен касательной плоскости к поверхности (3) (рис.1), т.е. будет являться нормальным вектором к этой поверхности. И уравнение касательной плоскости к поверхности (3), проведенной через точку P₀(x₀, y₀, z₀) имеет вид:

Fx′(x0, y0, z0)(x - x0) + Fy′(x0, y0, z0)(y - y0) + Fz′(x0, y0, z0)(z - z0) = 0.

(4)

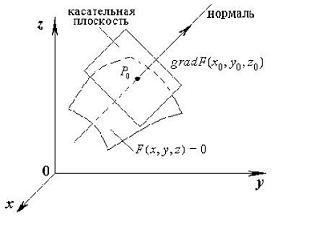
Рис. 1