Министерство образования Республики Беларусь

Учреждение образования

«Белорусский государственный университет информатики и радиоэлектроники» Кафедра экономики

Самостоятельная работа по курсу

“Прогнозирование и планирование в экономике”

на тему:

Выполнил:

Проверил:

канд.экон.наук, доцент

Сак А.В.

Минск 2009

Цель

Изучение методов оценки точности и надежности прогнозов, получение практических навыков выбора трендовых моделей для прогнозирования.

Задание

Рассматривая динамический ряд, представленный таблицей, построить трендовую модель (вариант 6):

1. Степенная функция

2. Полином 3-ей степени (кубическая парабола)

3. Гипербола 3-ей степени

Осуществить прогнозирование для периодов упреждения τ = 1, 2, 3.

Провести необходимые расчеты ( ,ē²,К) и выбрать для прогнозирования наилучшую кривую (прогнозную модель), дающую наиболее точные значения прогноза.

В выводах обосновать выбор лучшей модели. Результаты представить графическим методом.

Исходный динамический ряд

t, годы	1997	1998	1999	2000	2001	2002	2003	2004	2005	2006	2007	2008	2009
yt, млн. руб.	560	608	685	807	839	914	1100	1196	1499	1574	1513	1610	1592

Степенная функция:

Полином 3-ей степени (кубическая парабола):

Гипербола 3-ей степени:

Ход работы

Трендовые модели для соответствующих кривых имеют вид:

1. Степенная

1. Прологарифмируем уравнение:

Введем обозначение:

a₀^’ = ln a₀

T = ln t

Получим:

Y_t=a₀^′+a₁T

2. Для нахождения параметров а₀^‘ и а₁ воспользуется формулами:

Для удобства подсчетов составим таблицу1:

Год	yt	t	T	T2	Yt	YtT
1997	560	1	0,00	0,00	6,33	0,00
1998	608	2	0,69	0,48	6,41	4,44
1999	685	3	1,10	1,21	6,53	7,17
2000	807	4	1,39	1,92	6,69	9,28
2001	839	5	1,61	2,59	6,73	10,84
2002	914	6	1,79	3,21	6,82	12,22
2003	1100	7	1,95	3,79	7,00	13,63
2004	1196	8	2,08	4,32	7,09	14,74
2005	1499	9	2,20	4,83	7,31	16,07
2006	1574	10	2,30	5,30	7,36	16,95
2007	1513	11	2,40	5,75	7,32	17,56
2008	1610	12	2,48	6,17	7,38	18,35
2009	1592	13	2,56	6,57	7,37	18,91
∑	14497	91	22,55216	46,15387	90,35321	160,144

По данным таблицы и формулам рассчитываем параметры а₀^′ и а₁:

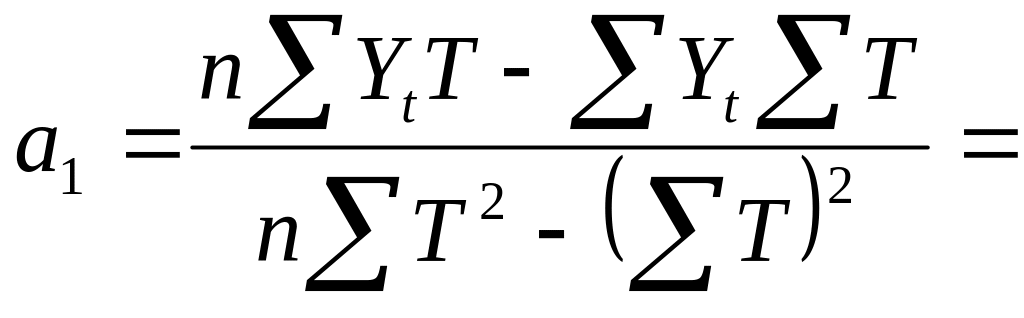0,48

a′₀=(Y_t-a₁T)/n= 6,11

Отсюда следует:

Y_t= 6,11+ 0,48∙T

Найдем а₀:

a₀=℮^а′ =443,95