2. Определение геометрических характеристик сечения

Разобьем сечение на три части (два прямоугольника и один полукруг).

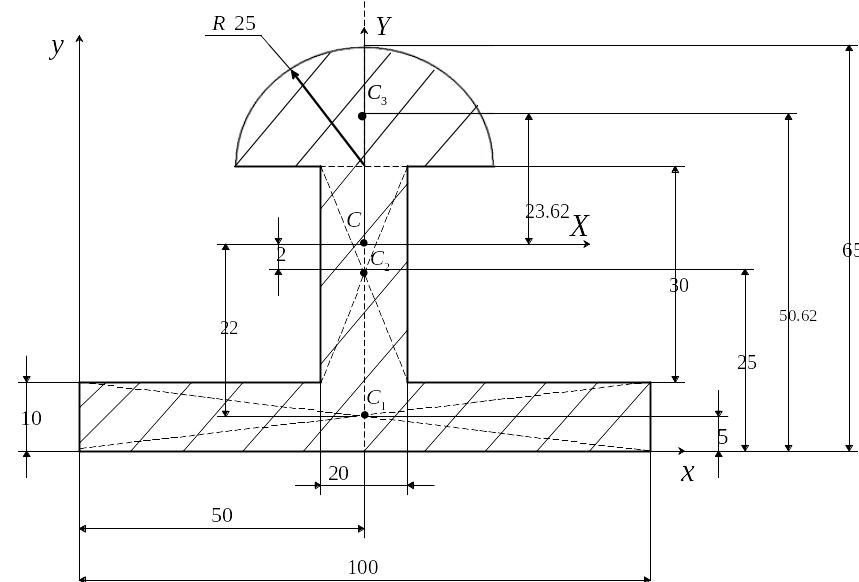
Рис. 5

Площади частей:

мм²; мм²; мм²

Определяем координаты центра тяжести и статические моменты:

мм

мм;

мм; мм

Применяя метод разбиения и формулы моментов инерции прямоугольников и полукруга относительно собственных центральных осей, а также теорему о моменте инерции относительно оси, параллельной центральной (теорему Гюйгенса- Штейнера), записываем:

Момент инерции J_х

мм⁴

мм⁴

мм⁴

492333 + 47400 + 699837.3 = 1239570.3 мм⁴

Моменты инерции J_у вычисляем как сумму моментов инерции прямоугольников и полукруга относительно центральной оси:

мм⁴

мм⁴

мм⁴

83333 + 20000 + 153320,3 = 1006653,3 мм⁴

Полярный момент инерции:

мм⁴

Расстояния от центральных осей до наиболее удаленных точек поперечного сечения:

мм , мм

Осевые моменты сопротивления:

Полярный момент сопротивления:

1. Расчет балки на растяжение-сжатие

3.1 Обоснование метода решения

Для определения продольных сил, нормальных напряжений и деформации применим метод сечений. Метод сечений предназначен для определения значений и направления действия внутренних сил.

Внутренние силы, распределенные по сечению, можно привести к главному вектору , приложенному в центре тяжести сечения и главному моменту . Каждый из этих векторов можно разложить на 3 компоненты по осям координат: 3 силы ( ) и 3 момента ( ), которые называются внутренними усилиями или силовыми факторами в поперечном сечении.

Названия внутренних усилий:

– продольная (осевая) сила, вызывающая деформацию растяжения или сжатия по оси стержня;

– поперечные (перерезывающие) силы, вызывающие сдвиг поперечных сечений относительно друг друга;

– изгибающие моменты в сечении относительно осей и , возникающие при изгибе в плоскостях и соответственно;

– крутящий момент, возникающий при взаимном повороте сечений вокруг оси стержня.

Гипотеза плоских сечений: поперечные сечения стержня плоские и перпендикулярные его продольной оси до деформации остаются плоскими и перпендикулярными к его оси и после деформации. В таком случае нормальные напряжения можно считать распределенными постоянно по сечению и формула для нормальных напряжений при одноосном растяжении-сжатии принимает вид

.

2. Составление расчетной схемы и аналитическое решение

Материал бруса – сталь Ст.3; МПа; кН; F=2581.25 мм²; ; ;

Разбиваем брус на участки 1(HF), 2(AH). Применяя метод сечений, рассматриваем равновесие правой части, отбрасывая при этом отсеченную левую часть.

Для участка 1(HF):

кН

Для участка 2(AH):

кН

Для построения эпюры нормальных напряжений, находим напряжения на каждом участке:

Эпюру перемещений строим, начиная от защемленного конца A.

мм

мм