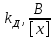Федеральное государственное автономное

образовательное учреждение

высшего образования

«СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ»

ИНСТИТУТ ИНЖЕНЕРНОЙ ФИЗИКИ И РАДИОЭЛЕКТРОНИКИ

Кафедра «Радиоэлектронные системы»

Курсовая работа

Система автоподстройки частоты

Преподаватель _________ Гарифуллин В.Ф.

подпись, дата

Студент РФ15-34 _________ Мутовин А.А.

подпись, дата

Красноярск 2018

Содержание

1 Исходные данные……………………………………………………………......3

2 Расчет параметров следящей системы…………………………………….…...3

2.1 Определение передаточной функции……………………………………....3

2.2 Определение спектральной плотности шума……………………………...3

3 Оптимизация следящей системы………………………………………….……4

3.1 Оптимизация следящей системы по параметру ………………………...4

3.2 Определение оптимального значения шумовой полосы………………….5

3.3 График зависимости ошибок от полосы пропускания схемы………….…6

4 Построение ЛАХ и ЛФХ разомкнутой системы………………………...…..…6

4.1 Логарифмическая амплитудно-частотная характеристика…………….…6

4.2 Логарифмическая фазо-частотная характеристика………………………..7

4.3 Определение запаса устойчивости…………………………………….…...8

5 Построение АЧХ замкнутой системы…………………………………….…....8

6 Моделирование следящей системы……………………………………….…....9

6.1 При ступенчатом воздействии………………....………...………………..11

6.2 При квадратичном воздействии……………….………………...………...12

7 Функциональная схема следящей системы……………...…………………...13

8 Список использованной литературы…………………...……………………..19

1 Исходные данные

Рисунок 1 – Структурная схема следящей системы 2-го порядка астатизма

Таблица 1 – Исходные данные

Номер варианта	Тип следящей системы	Порядок астатизма	Параметры задающего воздействия				Коэффициент передачи дискриминатора		Спектральная плотность шума		Параметры динамического звена
40	АПЧ	2	80	50	25	0.2		2∙10-4		0,2

2 Расчет параметров следящей системы

2.1 Определение передаточной функции

Найдем передаточные функции разомкнутой системы , а также замкнутой системы , используя параметры системы, описанные в задании.

Порядок астатизма системы , передаточная функция разомкнутой системы определяется по формуле:

(1)

Передаточная функция замкнутой системы:

(2)

2.2 Определение спектральной плотности шума

Используя правило преобразования структурных схем (перенос сумматора с выхода на вход звена), для спектральной плотности эквивалентного шума приведенного ко входу дискриминатора можно записать:

(3)

3 Оптимизация следящей системы

3.1 Оптимизация следящей системы по параметру

Оптимизация системы по критерию минимума среднего квадрата ошибки сводится к нахождению параметра , при котором обеспечивается минимум величины . Составляющая определяет динамическую ошибку, обусловленную инерционностью следящей системы по отношению к меняющемуся задающему воздействию, а составляющая определяет дисперсию ошибки , обусловленную помехой .

В данном случае порядок астатизма равен 2, следовательно, динамическая ошибка определяется как:

(4)

Случайная составляющая ошибки определяется статистическими характеристиками помехи n(t), структурой и параметрами системы. В качестве помехи используем модель белого шума с равномерной в полосе частот спектральной плотностью. Дисперсию шумовой ошибки рассчитываем по формуле:

	(5)
	(6)

где 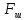– шумовая полоса следящей системы, – АЧХ замкнутой системы.

Выражение для комплексного коэффициента передачи замкнутой системы:

(7)

(8)

(9)

где:

(10)

(11)

Шумовая полоса системы:

(12)

Дисперсия шумовой ошибки:

(13)