
- •Содержание
- •Введение
- •1. Линейное программирование
- •1.1. Построение математической модели злп
- •1.2. Решение злп графическим методом:
- •1.3. Решение злп алгебраическим методом:
- •1.4. Решение злп симплекс – методом:
- •Решение методом искусственного базиса
- •3.Решить зцлп
- •3.1Решение зцлп методом Гомори:
- •3.1Целочисленное программирование. Метод ветвей и границ
- •4. Решение задачи булевского программирования о распределении капиталовложения.
- •4.2Булевское программирование. Метод Баллаша
- •5.1. Поиск локального минимума метом одномерной оптимизации
- •5.1.1 Метод дихотомии ( деление отрезка пополам ).
- •4.3 Уточнение решения задачи Методом золотого сечения.
- •4.4 Уточнение решения задачи методом квадратичной аппроксимации.
- •4. Поиск локального максимума функции
- •4.1. Метод нулевого порядка - метод Хука – Дживса
- •6.2 Метод найскорейшего спуска(Коши)
4.4 Уточнение решения задачи методом квадратичной аппроксимации.
Описание алгоритма метода последовательного оценивания с использованием квадратичной аппроксимации :
1 Пусть f(x) – оптимизируемая функция, х1 – начальная точка, х – величина шага по оси абсцисс. Вычислить х2 = х1+х и значения функции f(x1) и f(x2).
2 Если f(x1) >f(x2), то положить х3 = х1 +2 х. Если f(x1) f(x2), то положить х3 = х1 -х.
3 Вычислить значение функции f(x3). Найти fmin = min{ f(x1), f(x2), f(x3)}, xmin – точка, которой соответствует fmin.
4
По трем точкам x1,
x2,
x3
вычислить
![]() по формуле
по формуле
![]() .
.
5
Произвести проверку на окончание поиска
минимума. Если разности
![]() и
и
![]() являются достаточно малыми величиннами,
то закончить поиск; иначе перейти к п.
6.
являются достаточно малыми величиннами,
то закончить поиск; иначе перейти к п.
6.
6
Выбрать «наилучшую» точку (![]() или
)
и две точки по обе стороны от нее.
Обозначить эти точки в естественном
порядке и перейти к п. 3.
или
)
и две точки по обе стороны от нее.
Обозначить эти точки в естественном
порядке и перейти к п. 3.
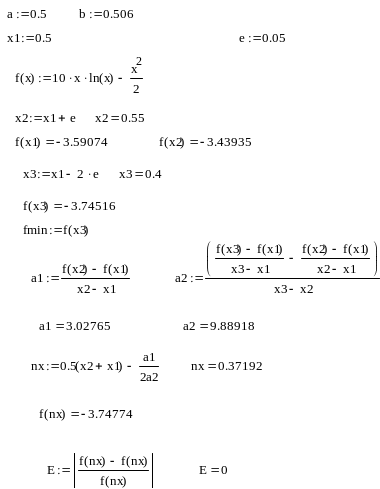
В
итоге мы вычислили минимальное значение
функции на заданном отрезке [0.5 ; 1], с
точностью
![]() ,
оно находиться в точке x1
= 0,5 ; f(x)
= – 3,59074 ;
,
оно находиться в точке x1
= 0,5 ; f(x)
= – 3,59074 ;
4. Поиск локального максимума функции
4.1. Метод нулевого порядка - метод Хука – Дживса
Метод Хука-Дживса был разработан в 1961 году, но до сих пор является весьма эффективным и оригинальным. Поиск состоит из последовательности шагов исследующего поиска вокруг базисной точки, за которой в случае успеха следует поиск по образцу. Он применяется для решения задачи минимизирования функции без учета ограничений.
![]() a=0
b=8 X0[0;0]
e=0,3 e=0,5
a=0
b=8 X0[0;0]
e=0,3 e=0,5


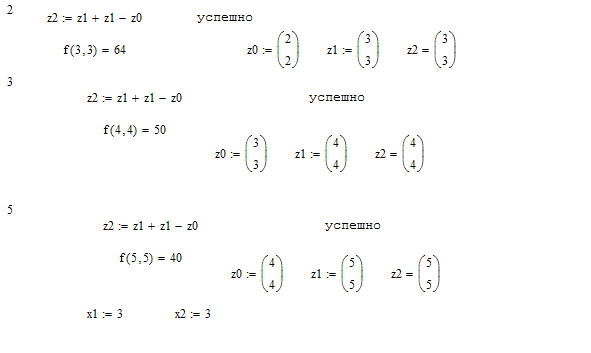
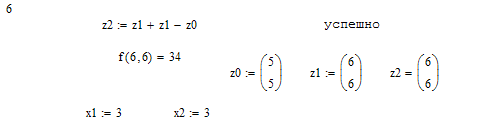
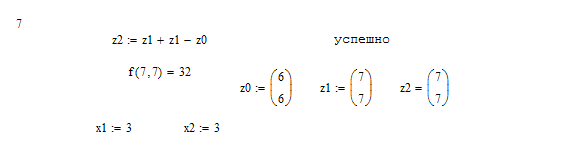


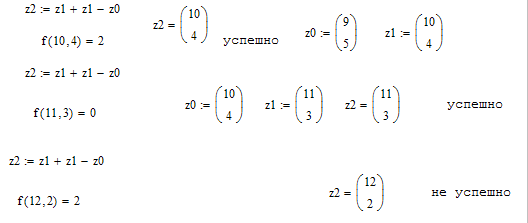

6.2 Метод найскорейшего спуска(Коши)
Алгоритм
Шаг 1. Задать X0, ε1>0, ε2>0, предельное число итераций M. Найти градиент функции в произвольной точке.
Шаг 2. Положить k=0.
Шаг
3. Вычислить
![]()
Шаг
4. Проверить
выполнение критерия окончания
![]() :
:
а) если критерий выполнен, то X*=Xk;
б) иначе перейти к шагу 5.
Шаг 5. Проверить выполнение равенства k≥M:
а) если неравенство выполнено, то X*=Xk;
б) иначе перейти к шагу 6.
Шаг
6. Вычислить
величину αk
в соотношении
![]() на основе метода полиномиальной
аппроксимации, положив αk1=0,
Δα=0,1.
на основе метода полиномиальной
аппроксимации, положив αk1=0,
Δα=0,1.
Шаг 7. Вычислить .
Шаг 8. Проверить выполнение условий:
![]() а)
если оба условия выполнены, то расчет
окончен и X*=Xk+1;
а)
если оба условия выполнены, то расчет
окончен и X*=Xk+1;
б) если хотя бы одно из неравенств не выполнено, то положить k=k+1 и перейти к шагу 3.
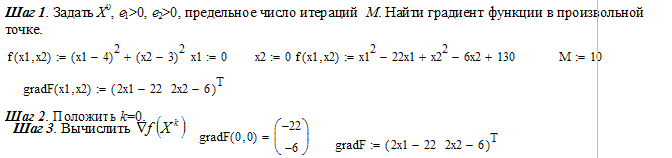


Заключение
В ходе курсовой работы были углублены теоретические знания по дисциплине, а также приобретены и закреплены практические навыки решения задач линейного и оценке эффективности работы применяемых алгоритмов.
В ходе курсовой работы были изучены задачи линейного программирования, целочисленного линейного программирования и различные алгоритмы их решения. Результаты, полученные различными методами, совпадают, что говорит о корректности решения.
Так же изучены методы безусловной оптимизации и поиска глобального экстремума функция. Как и в предыдущем случае, результаты, полученные различными методами, совпадают, что говорит о корректности решения.
Список использованной литературы
1. Методические указания для изучения дисциплины «Прикладная математика» для студентов специальности «Компьютерные системы и сети» Раздел «Решение задач целочисленного линейного программирования» дневной и заочной форм обучения/ Сост. Балакирева И.А., Скатков А.В.– Севастополь: Изд-во СевНТУ, 2000. –13 с.
2. Методические указания к индивидуальным занятиям и подготовке к курсовой работе по разделу «Решение задач линейного программирования и анализ оптимального решения на ЭВМ» дисциплины «Прикладная математика» для студентов специальности 7.091501 «Компьютерные системы и сети» дневной формы обучения /Сост. Л.П. Луговская, Н.А. Скаткова. – Севастополь: Изд-во СевНТУ, 2009. – 15 с.
3. Реклейтис Г., Рейвиндран А., Регсдел К. Оптимизация в технике: в 2-х томах. Пер. с англ./ Г. Реклейтис,- М.: Наука, 1984.- Т.1.- 352 с. – Т.2.- 320 с.
