Задачи на случайные величины / Fedya_TV i MS

Савельев Ф. Г.

Гр. 2351

Вариант 19.

Дано:

1. Вычисление вектора мат. Ожиданий и ковариационных характеристик С.В.

Сначала найдём неизвестную константу. Для этого вычислим плотность распределения одной из компонент случайного вектора с учётом неизвестной константы C и приравняем её к единице.

.

Найдём вектор математических ожиданий

Имеем: .

Плотность распределения :

Плотность распределения :

Отсюда, - вектор мат. ожиданий.

Ковариационную матрицу мы можем найти двумя способами

1-ый способ. Ковариационная матрица – это матрица, обратная матрице квадратичной формы.

Матрица квадратичной формы: ;

Матрица ковариации: .

2-ой способ. Найдем первый и четвертый элемент матрицы ковариации – это дисперсии компонент случайного вектора x и y соответственно.

,

Остается найти второй и третий члены матрицы. Они, как известно, равны между собой и вычисляются по формуле: .

Найдем .

Тогда второй и третий элементы будут равны: .

Имеем матрицу ковариации: 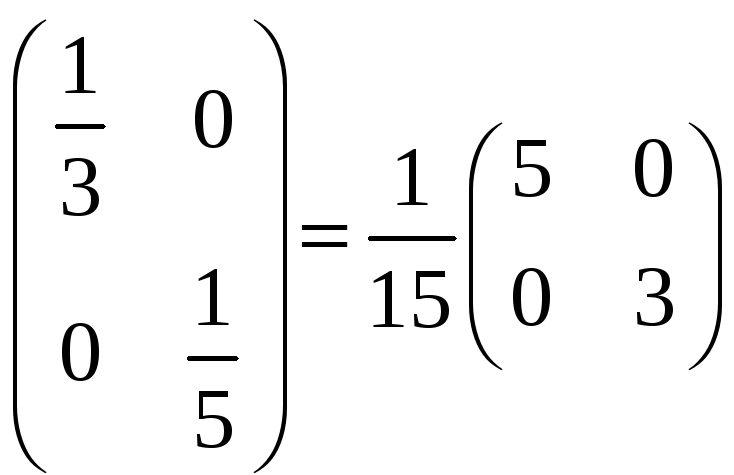, что полностью совпало с вычисленным первым способом.

2. Найти ортогональное преобразование, переводящее соответствующий центрированный случайный вектор в вектор с независимыми компонентами.

Преобразование будет называться ортогональным, если его матрица будет ортогональна т. е.

Тогда само преобразование можно описать формулой

- матрица - вектор при этом матрица должна быть ортогональной.

Однако нам в задании уже дана плотность с независимыми компонентами, следовательно для перевода данного случайного вектора в центрированный вектор необходим лишь сдвиг. Опишем общий вид данного преобразования.

Матрица - матрица перехода от стандартного базиса к базису собственных векторов нашей матрицы квадратичной формы.

Матрица квадратичной формы уже диагональная и собственные числа равны, соответственно,

Матрица перехода будет - единичная матрица. Эта матрица ортогональна, следовательно, ортогонально и преобразование. Для центрирования данного случайного вектора необходимо просто отнять столбец математических ожиданий данных компонент.

Произведём первую замену. Вместе , подставляем новые координаты

Тогда квадратичная форма будет следующей

Якобиан такой замены будет равен 1

Следовательно, после такой замены, плотность случайного вектора принимает вид

Данный вектор центрирован (математическое ожидание обоих компонент равно 0), имеет независимые друг от друга компоненты и получен ортогональным преобразованием.

Из такого вектора легко получить стандартный нормальный вектор. Достаточно сделать ещё одну замену. Вместо , ставим

На диагонали всегда будут находиться члены вида . Якобиан такой замены также можно очень просто посчитать

И умножив плотность распределения т. е. компонент предыдущей замены получим

плотность распределения стандартного и центрированного вектора.

4. Вычислить характеристики совместного распределения с.в. и записать его плотность.

Математические ожидания мы находим, используя свойство его линейности.

Пусть , тогда ,

.

Находим новые дисперсии, используя свойства линейности для независимых компонент.

Для заданного случайного вектора компоненты уже независимы, следовательно, мы можем найти дисперсию так:

Из ранее найденного имеем:

Тогда можно вычислить .

Аналогично, имеем для дисперсии Y:

.

Вычислим матрицу ковариации

,

Надо вычислить ковариации новых компонент вектора.

.

для наших независимых компонент равно 0.

Отсюда, матрица ковариации в явном виде:

.

Записываем плотность нового случайного вектора

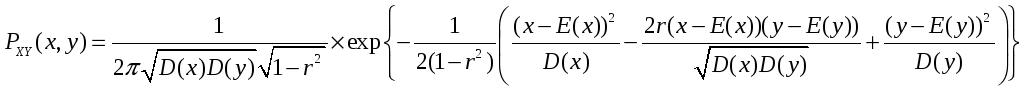
где .

Подставив все значения, получим:

.

Для проверки распределения составим матрицу квадратичной формы,

Возведем ее в (-1)-ую степень, получили матрицу ковариации, что показывает верность наших расчетов.