2. Доказать свойство катета, лежащего против угла в 30°.
Теорема о свойстве катета, лежащего против угла в 30 (прямая). Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы.
Дано:
∆АВС:
Доказать:
Доказательство:
1. Дополнительное построение: Приложим к авс равный ему авd так, чтобы стороны ав совместились, а стороны ad и ас составили прямую линию.
2.
Рассмотрим полученный BCD.
BCD
- равнобедренный по признаку
BC = CD.
3.
Билет 22
Опр1. Кругом называется часть плоскости, ограниченная окружностью. Круг радиуса R с центром в точке О содержит точку О и все точки плоскости, находящиеся от точки О на расстоянии, не большем R.
Формула площади круга. Площадь S круга радиуса R выражается формулой S = R2.
Опр2. Круговым сектором называется часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.
Формула
площади сектора. Площадь сектора
равна произведению длины его дуги
на половину радиуса:
Из чертежа очевидно, что площадь сектора зависит от градусной меры центрального угла, образованного радиусами, ограничивающими данный сектор. Она может быть определена как соответствующая часть площади круга.
Площадь
сектора с центральным углом в 1°
составляет 1/360 часть площади круга,
а площадь сектора с центральным углом
в °
составляет
часть площади круга и определяется
по формуле:
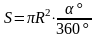Преобразуем
полученную формулу:
Следует заметить, что площадь сектора однозначно определяется величиной центрального угла. Чем больше центральный угол сектора, тем больше длина дуги и, соответственно, площадь сектора.
Определение 3. Сегментом называется часть круга, ограниченная дугой и хордой, соединяющими концы этой дуги.
Любая хорда разбивает круга на два сегмента.
Теорема 1: В треугольнике против большей стороны лежит больший угол.
Дано: ∆АВС; AB > AC.
Доказать:
Доказательство:
Отложим на стороне АВ отрезок AD = AC. AB > AD, точка D AB. Сл-но, ACD - часть ACB и ACD < ACB.
ADC – внешний угол треугольника ∆BDC, поэтому ADC > B.
∆ABC – равнобедренный по построению (AD = AC). Следовательно, ACD = ADC.
Теорема 2: В треугольнике против большего угла лежит большая сторона.
Дано: ∆АВС;
Доказать: AB > AC.
Доказательство от противного:
Предположим, что это не так. Тогда либо АВ = АС, либо АВ < AC.
В первом случае ∆АВС – равнобедренный C = B.
Во втором случае C < B (против большей стороны лежит больший угол).
И то, и другое противоречит условию Следовательно, наше предположение неверно, AВ > AC.
Следствия из теорем.
Следствие 1: В тупоугольном треугольнике против тупого угла лежит наибольшая сторона.
Тупой угол больше острого. Следовательно, сторона, лежащая против тупого угла, больше стороны, лежащей против острого угла.
Следствие 2: В прямоугольном треугольнике гипотенуза больше катета.
Гипотенуза лежит против прямого угла, а катет – против острого. Так как прямой угол больше острого, то гипотенуза больше катета.
Следствие 3: Если два угла треугольника равны, то треугольник равнобедренный (признак равнобедренного треугольника).
Пусть в треугольнике два угла равны. Тогда равны и стороны, лежащие против этих углов. Действительно, если предположить, что одна из указанных сторон больше другой, то угол, лежащий против нее, будет больше угла, лежащего против другой стороны, а это противоречит условию (тому, что данные углы равны). Итак, если в треугольнике две стороны равны, то треугольник равнобедренный.
Билет 23
Исследуем взаимное расположение окружности с центром в точке О и прямой.