
- •1. Пусть а1в2с2 – треугольник, равный треугольнику авс, с вершиной в2 на луче а1в1 и вершиной с2 в той же полуплоскости относительно прямой а1в1, где лежит вершина с1.
- •5. Треугольник а1в1с1 совпадает с треугольником а1в2с2, а значит ,равен треугольнику авс.
- •1. Дополнительное построение. Проведем отрезок bd – биссектрису авс.
- •1) А, где а – точка, являющаяся вершиной угла;
- •2) Вас, где а – точка, являющаяся вершиной угла, в и с – точки, взятые на разных сторонах угла (ав и ас – лучи, образующие угол);
- •3) (Ab), где a, b – лучи, образующие угол.
- •1. По свойству касательных осq, obp. Проведем луч из точки а через центр окружности. 2. Рассмотрим образовавшиеся треугольники аос и аов.
- •1. Пусть серединные перпендикуляры kk1 и nn1 пересекаются в точке о. Соединим точку о с вершинами треугольника авс.
- •1. Пусть биссектрисы аа1 и вв1 пересекаются в точке о. Построим из точки о перпендикуляры ok, on и op к сторонам ав, вс и ас треугольника.
- •4. Рассмотрим полученные углы.
- •1) Остроугольные – все углы меньше 90;
- •2) Прямоугольные – один угол равен 90, два других острые;
- •3) Тупоугольные – один угол больше 90 (тупой), два других острые.
- •1. Пусть а1в2с2 – треугольник, равный треугольнику авс,
- •4. Отсюда следует, что вершина с2 совпадает с вершиной с1.
- •5. Треугольник а1в1с1 совпадает с треугольником а1в2с2, а значит, равен треугольнику авс.
- •3) Рассмотрим ∆aho и ∆bh1o.
- •2) И являются внутренними накрест лежащими
- •2) И являются внутренними накрест лежащими
- •1. Дополнительное построение. Проведем отрезок bd – биссектрису авс.
- •2. Определение внешнего угла треугольника. Доказать свойства внешнего угла треугольника.
- •2. Доказать свойство катета, лежащего против угла в 30°.
- •1. Дополнительное построение: Приложим к авс равный ему авd так, чтобы стороны ав совместились, а стороны ad и ас составили прямую линию.
- •1) Прямая p пересекает окружность
- •2. Пусть р – любая прямая и точка а не лежит на ней. Через точку а проведем прямую, перпендикулярную к прямой р.
- •1.Окружности не имеют общих точек. Проведем отрезок, соединяющий центры окружностей (о1о2) – линию центров.
- •3. Окружности имеют одну общую точку (окружности касаются).
- •2. Доказать неравенство треугольника.
- •1. Дополнительное построение:
- •2. Рассмотрим вcd:
- •1) Окружность – это геометрическое место точек, равноудаленных от данной точки.
- •2) Биссектриса угла – это геометрическое место точек, равноудаленных от сторон угла.
- •3) Серединный перпендикуляр к отрезку – это геометрическое место точек, равноудаленных от концов отрезка.
- •2 Определение вертикальных углов. Доказать свойство.
- •5. Oa и od – дополнительные полупрямые ok и on – дополнительные полупрямые n ko.
2. Определение внешнего угла треугольника. Доказать свойства внешнего угла треугольника.
Определение: Внешним углом треугольника называется угол, смежный с каким-нибудь внутренним углом треугольника.
Построение внешнего угла: Чтобы построить внешний угол треугольника, нужно продлить соответственную сторону треугольника. При каждой вершине треугольника можно построить два внешних угла. Они равны между собой, так как являются смежными с одним и тем же углом.
Теорема: Внешний угол
треугольника равен сумме двух внутренних углов треугольника, не смежных с ним.
Дано: ∆АВС.
Доказать:
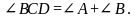
Доказательство:

Билет 20
Опр1.Расстоянием между двумя точками является длина отрезка, соединяющего эти точки на плоскости. Длина отрезка АВ – расстояние между точками АиВ.
Опр 2. Расстоянием от точки до прямой является длина перпендикуляра, опущенного из точки на прямую. CN n. Длина отрезка CN - расстояние от точки C до прямой n.
Опр3. Расстоянием между параллельными прямыми a и b является длина перпендикуляра, опущенного из произвольной точки прямой а
(точки Р) на прямую b. PQ b.
Теорема 1. Две прямые, перпендикулярные к третьей прямой, параллельны.
Дано: aс, b.с доказать, что аIIв
Допустим что а не паралл в, значит они пересекаются в т А. значит через т А к прямой опущены два перпендикуляра к прямой, что противоречит теореме о единственности прямой перпендикулярной данной .
Теорема 2. Если две прямые параллельны третьей прямой, то они параллельны между собой.

Дано: a II с; b II c.
Доказать: a II b.
Доказательство:
Допустим, что a ∩ b = {M}. Тогда через точку М проходили бы две прямые (прямые а и b), параллельные прямой c. Это противоречит аксиоме параллельных прямых. Значит, прямая a параллельна прямой b.
2. 1 Если два катета одного треугольника соответственно равны двум катетам другого треугольника, то такие прямоугольные треугольники равны (частный случай первого признака равенства треугольников).

2. Если катет и прилежащий острый угол одного треугольника соответственно равны катету и прилежащему острому углу другого треугольника, то такие прямоугольные треугольники равны (частный случай второго признака равенства треугольников).
3. Если гипотенуза и острый угол одного треугольника соответственно равны гипотенузе и острому углу другого треугольника, то такие прямоугольные треугольники равны.

─ следствие из второго признака равенства треугольников.
4. Если катет и противолежащий острый угол одного треугольника соответственно равны катету и противолежащему острому углу другого треугольника, то такие прямоугольные треугольники равны (частный случай второго признака равенства треугольников).
Доказывается аналогично предыдущей теореме ─ следствие из II признака равенства треугольников.
5. Если гипотенуза и катет одного треугольника соответственно равны гипотенузе и катету другого треугольника, то такие прямоугольные треугольники равны

.
Доказательство:
1. Так как С = С1, то треугольник АВС можно наложить на треугольник А1В1С1 так, что вершина С совместится с вершиной С1, а стороны СА и СВ наложатся соответственно на лучи СА1 и СВ1.
2. Так как СА = С1А1, то вершина А совместится с вершиной А1. Остается доказать, что совместятся точки В и В1.
3. Предположим, что точки В и В1 не совместятся. Рассмотрим Δ А1В1В2 – равнобедренный, так как АВ = A1B1 А1В2 = A1B1. Тогда A1B1В2 = A1В2B1. Заметим, что A1B1С1 - острый угол прямоугольного треугольника А1В1С1, а A1B1В2, смежный с ним, - тупой. Поскольку в треугольнике не может быть двух тупых углов, то это невозможно. Значит, точки В и В1 совместятся.
Билет 21
О пр1.
Окружностью
называется
геометрическая фигура, состоящая из
множества точек, равноудаленных от
данной точки. Эта точка называется
центром окружности.
О – центр окружности.
пр1.
Окружностью
называется
геометрическая фигура, состоящая из
множества точек, равноудаленных от
данной точки. Эта точка называется
центром окружности.
О – центр окружности.
Опр 2. Радиусом окружности называется отрезок, соединяющий любую точку окружности с ее центром, а также длина этого отрезка. ОС, ОА, ОВ – радиусы окружности.
Опр 3. Отрезок, соединяющий две точки окружности, называется хордой. PQ, АВ – хорды.
Опр 4. Наибольшая хорда окружности, проходящая через центр окружности, называется диаметром. Диаметр равен двум радиусам. АВ – диаметр.
Опр 5. Дугой окружности называется часть окружности, ограниченная двумя точками окружности. АС, АP, PQ, ВQ, BC – дуги окружности.
Формула длины окружности. Длина С окружности радиусом R выражается формулой С = 2R.
Формула
длины дуги окружности). Длина дуги
окружности определяется по формуле

Так
как длина окружности С = 2R,
то длина дуги в 1°
 а длина дуги в °
а длина дуги в °
Определение 1. Угол, вершина которого лежит в центре окружности, называется центральным углом.
Центральному углу АОВ соответствует АKВ.
Дугу окружности можно измерить в градусах. Если дуга АВ меньше полуокружности, то ее градусная мера равна градусной мере центрального угла АОВ. Если дуга АВ больше полуокружности, то ее градусная мера равна 360° − АОВ.
Сумма градусных мер двух дуг с общими концами равна 360°.
