Квартиль

Первый квартиль вычисляется по формуле:

–        нижняя граница квартильного интервала,

–        величина квартильного интервала,

–        номер квартильного признака,

–        сумма накопленных частот (весов) в интервалах, предшествующих квартильному,

–        частота квартильного интервала.

Аналогично рассчитывается третий квартиль. Второй же квартиль равен медиане.

Дециль

Рассчитывается по аналогии с расчетом квартиля. Можно найти девять децилей.

Средняя должна исчисляться не просто тогда, когда есть вариация признака, а тогда, когда мы располагаем качественно однородным вариационным рядом. Среднюю как обобщающую характеристику нельзя применять к таким совокупностям, отдельные части которых подчиняются различным законам распределения (или) развития в отношении величины распределяемого признака.

17. Понятие вариации и показатели ее размера.

Необходимость расчета показателей вариации

Средняя представляет собой обобщающую статистическую характеристику, в которой получает количественное выражение типичный уровень признака, которым обладают члены изучаемой совокупности. Но одной средней нельзя отобразить все характерные черты статистического распределения. Возможны случаи совпадения средних арифметических при разном характере распределения.

Показатели вариации используются для характеристики и упорядочения статистических совокупностей.

Абсолютные показатели вариации

Для измерения размера вариации используются следующие абсолютные показатели: размах, среднее линейное отклонение, дисперсия, среднее квадратическое отклонение.

Самым элементарным показателем вариации признака является размах вариации R. Размах вариации показывает лишь крайние  (min, max) отклонения признака от общей средней.

Для анализа вариации необходим показатель, который отражает все колебания варьирующего признака и дает обобщенную характеристику.

Среднее линейное отклонение (средняя арифметическая абсолютных значений отклонений - модуль отклонений отдельных вариантов от их средней арифметической):

1. для несгруппированных данных (простое)

2. для сгруппированных данных (взвешенное)

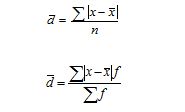
Дисперсия  признака - средний квадрат отклонений вариантов от их средней величины, она вычисляется по формулам простой и взвешенной дисперсий:

1. Простая дисперсия для несгруппированных данных

2. Взвешенная дисперсия для вариационного ряда

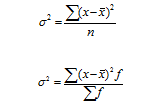
Cвойства дисперсии:

1. если все значения признака уменьшить или увеличить на одну и ту же постоянную величину А- дисперсия не изменится; 

2. если все значения признака уменьшить или увеличить в одно и то же число раз (k раз), то дисперсия уменьшится или увеличится в k²  раз.

Используя второе свойство дисперсии, можно получить формулу вычисления дисперсии в вариационных рядах с равными интервалами по способу моментов:

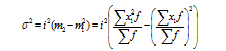
где  i – величина интервала, X₁ - новые (преобразованные) значения вариантов (А – условное начало, в качестве которого удобно использовать середину интервала или величину признака, обладающего наибольшей частотой.                   

                                                                    

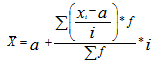
1. Момент второго порядка

2. Квадрат момента первого порядка

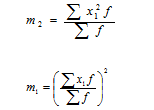
Среднее квадратическое отклонение равно корню квадратному из дисперсии:

1. для несгруппированных данных (простое)

2. для вариационного ряда по сгруппированным данным (взвешенное)

Среднее квадратическое отклонение показывает, на сколько в среднем отклоняются отдельные варианты от их среднего значения.

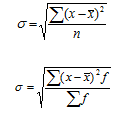
Относительные показатели вариации

Для характеристики меры колеблемости изучаемого признака исчисляются показатели колеблемости в относительных величинах.  Они позволяют сравнивать характер рассеивания в различных распределениях  (различные единицы наблюдения одного и того же признака в двух совокупностях, при различных значениях средних,  при сравнении  разноименных  совокупностей). Расчет  показателей меры относительного рассеивания осуществляют как отношение абсолютного показателя рассеивания к  средней  арифметической, умноженное на 100%.

1. Коэффициент  осцилляции  отражает  относительную  колеблемость крайних значений признака вокруг общей средней.

2. Относительное линейное отклонение характеризует долю усредненного значения абсолютных отклонений (модуль отклонений) от средней величины.

3. Коэффициент вариации - отношение среднего квадратического отклонения к средней арифметической, применяется для сравнения вариаций различных признаков, используется как характеристика однородности совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33%.

18. Дисперсия альтернативного признака.

Среди варьирующих признаков, которые изучает статистика, встречаются признаки, которые проявляются в том, что у одних единиц совокупности эти признаки наблюдаются, у других нет. Иными словами: альтернативный признак - это такой единственный признак, который может принимать единица совокупности из всех возможных вариантов. Если рассматривать продукцию по категориям (сортам), то она может быть либо   только  I  категории (сорта),  либо только II категории (сорта) - в данном контексте следует рассматривать эти признаки как два противоположных события.  Признаки, которыми обладают одни единицы и не обладают другие, называются альтернативными. Количественно вариация альтернативного признака в численности всей совокупности обозначается p,  а доля единиц, не обладающих этим признаком, обозначается q  и принимает значения: p=1, q=0

Дисперсия и среднее значение для доли альтернативного признака (см. Статистическая проверка гипотез)