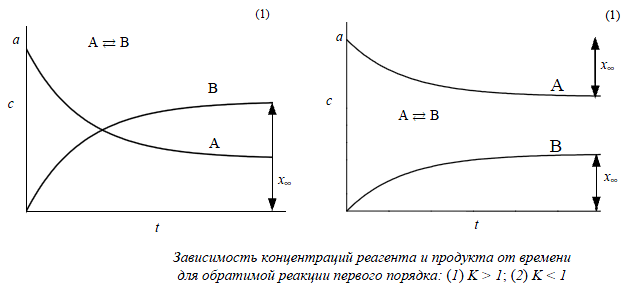
2. Принцип независимости химических реакций. Составление и решение кинетических уравнений для обратимых реакций первого порядка.

При изучении кинетики сложных реакций, включающих несколько элементарных стадий, используют принцип независимости химических реакций: если в системе протекает несколько простых реакций, то каждая из них подчиняется основному постулату химической кинетики независимо от других реакций.

Обратимые реакции:

Эта схема описывает реакции изомеризации в газовой фазе или в растворе, например: цис-стильбен транс-стильбен, бутан изобутан.

Закон действующих масс записывается следующим образом:

Если начальные концентрации веществ A и B обозначить, соответственно, a и b и ввести степень превращения x ([A] = a – x, [B] = b + x), то кинетическое уравнение приобретает вид:

Решение этого уравнения можно выразить через степень превращения, соответствующую достижению равновесия:

,

где x_∞ определяется условием равенства скоростей прямой и обратной реакций:

Уравнения для обратимой реакции первого порядка имеют такой же вид, как и для необратимой реакции с той разницей, что вместо начальной концентрации фигурирует равновесная, а константу скорости необратимой реакции заменяет сумма констант для прямой и обратной реакций.

При t →∞ наступает равновесие, которое характеризуется константой:

4. Давления пара над чистым веществом и теплота фазового перехода.

μ_i(p_i)= μ_i^ø + RT ln(p_i/p^o); ΔU = Q_ф.пер + рΔV. d(lnp)/dT=ΔHф.п/RT²

Билет 12.

1. Водородная связь и её характеристики. Влияние водородной связи на свойства органических веществ.

2. Химический потенциал, определение. Идеальные растворы. Термодинамика смешения. Активность и коэффициенты активности.

Зависимость термодинамических потенциалов от их естественных переменных описывается основными уравнениями термодинамики – фундаментальными уравнениями Гиббса. В дифференциальной форме

эти уравнения имеют вид:

где химический потенциал

характеризует приращение соответствующего термодинамического потенциала при изменении количества данного вещества и постоянстве естественных переменных и количеств остальных веществ. Равенство химических потенциалов веществ является признаком их химического равновесия; разность химических потенциалов является движущей силой при массопереносе.

Удобной системой сравнения свойств раствора является идеальный раствор. Под идеальным обычно понимают раствор, для компонентов которого при всех составах и температурах выполняется закон Рауля.

Согласно закону Рауля, давление пара растворителя pi над раствором пропорционально мольной доле растворителя xi в растворе:

p_i=p_i^sx_i,

где p_i – давление насыщенного пара компонента над раствором, p_i^s – давление насыщенного пара над чистым компонентом, x_i – мольная доля i-го компонента в растворе.

Признаком идеальности раствора является аддитивность парциальных давлений, парциальных объемов, теплоемкостей и энтальпий компонентов. Тепловой эффект при образовании идеального раствора равен нулю, объем не изменяется, а энтропия равна идеальной энтропии смешения.

Для описания свойств реальных растворов вводится понятие активности. Активность a_i – безразмерная величина, определяемая через разность химических потенциалов этого вещества в данной фазе и в стандартном состоянии:

Если пар вещества ведет себя как идеальный газ, то активность можно определить через экспериментально измеряемые величины:

где p_i – давление насыщенного пара i-го компонента над раствором, p_i^s – давление насыщенного пара чистого i-го вещества при той же температуре T и в том же фазовом состоянии, что и раствор.

Активность a_i выражается в виде произведения мольной доли xi компонента на его коэффициент активности γ_i:

a_i = γ_ix_i.

Если активность выражать через разные концентрации, соответственно, будет изменяться и значение коэффициента активности γ:

a = γ_xx = γ_cc = γ_mm.

Коэффициенты активности – безразмерные величины, характеризующие работу, которую надо совершить при перемещении i-го компонента из идеального раствора в реальный при постоянной температуре, давлении и концентрации. В зависимости от выбранной системы сравнения, коэффициенты активности компонентов определяют на основании отклонений парциальных давлений паров компонентов от закона Рауля или от закона Генри.