1.5 Структурна схема математичної моделі узагальненої машини

Структурну схему складемо на підставі СДР для координатної системи u, v, 0 узагальненої двофазної машини, тобто узагальнену структурну схему. Таку структуру можна набрати на екрані дисплея згідно з програмою SIAM, або вирішувати повну СДР чисельним методом згідно з програмою MATCAD. Структура (рис.1.6) має вигляд:

На рис.1.6 умовні позначення великих літер означають: А=_s_o; B=_sK_r_o; C=_s_o; D=_sK_r_o;

Рисунок 1.6 – Структурна схема двофазної моделі АД в узагальненій

системі координат u, v, 0

1.6 Теоретичні особливості сдр синхронних двигунів (сд)

В загальному вигляді СД може розглядатися як трифазна явнополюсна машина, тобто статор – 3 фази, ротор – однофазна обмотка збудження постійного струму, m-фазна демпферна (або пускова) обмотка.

Як завжди СДР складається з рівнянь електричної рівноваги всіх контурів статора та ротора, рівняння електромагнітного момента, та рівняння Даламбера.

Принципова схема СД має вигляд рис.1.7.

Рисунок 1.7 – Координатна схема СД

а кут _кt=t, тобто розглядаємо СДР в координатній системі d, q, 0, для якої _к=. Проекції векторів, що співпадають з позитивним напрямком осей фаз А; В; С, є також позитивні. Вісь q (або V) випереджає вісь d (поздовжню). Диференційні рівняння для контурів статора аналогічні як і для АД, тобто:

Для контура обмотки збудження

Для пускової (демпферної) обмотки, зважаючи на те, що є суттєва несиметрія по осях d, q (R_dR_q) записується окремо рівняння для еквівалентної демпферної обмотки по осі d, а також – по осі q, а саме:

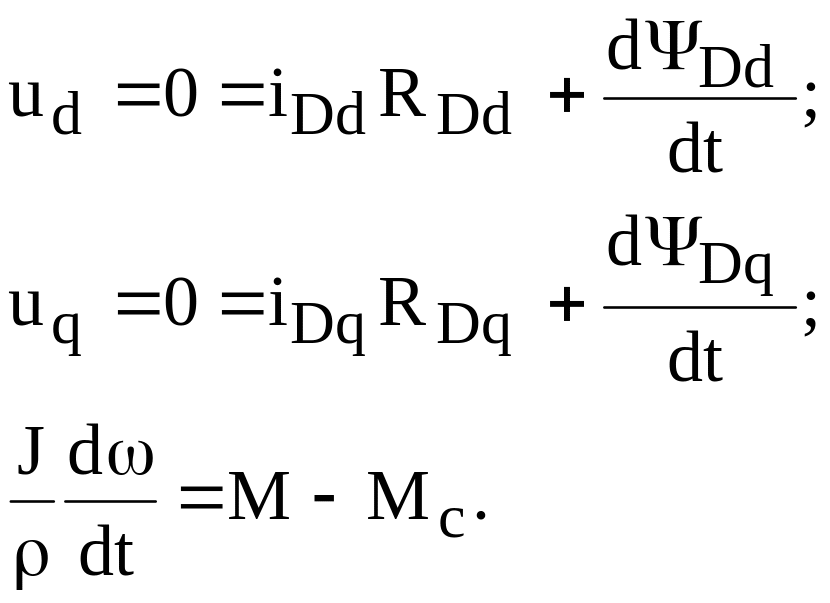
(Потрібно також мати залежність М=f(_А ;_В…), якщо аналізується електромагнітний перехідний процес та електромеханічний).

Кожна з фаз СД (А; В; С; f; Dd та Dq) створює своє повне потокозчеплення (як і для АД) зі струмами всіх контурів (і_А; і_В; і_С; і_f; і_Dd та і_Dq). Це означає, що для СД записується система з 6-ох алгебраїчних рівнянь потокозчеплень виду _ф1=L_ф1і_ф1+М_{ф1 ф2}і_ф2+ і т.п.

Всі індуктивності фаз статора та ротора, а також взаємоіндуктивності між фазами як статора, так і ротора є функції геометричних координат. Це буває тоді, коли з обертанням ротора конфігурація магнітного поля міняється в залежності від положення ротора.

Індуктивності фаз є періодичними функціями кута  (між осю А та d),  саме [ ]:

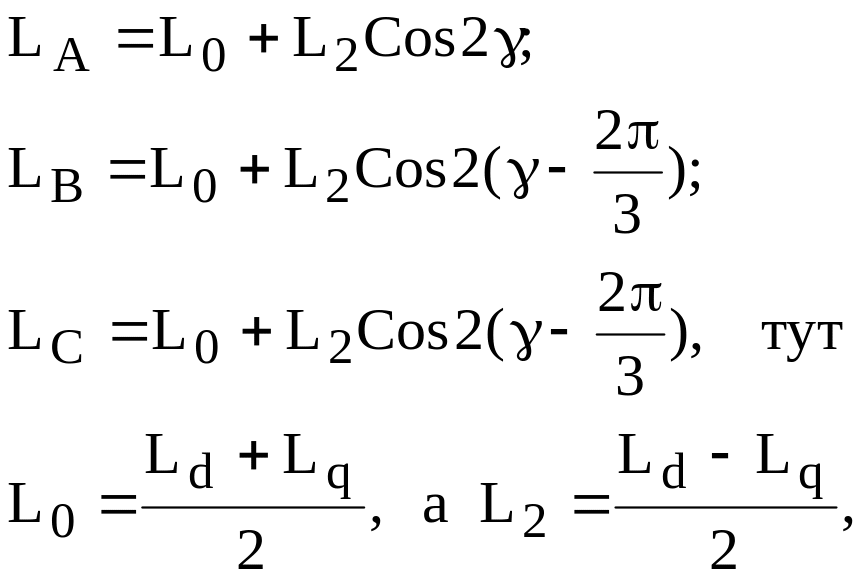
де L_d – максимальне значення індуктивності фази коли її вісь співпадає з осю d, L_q – мінімальне значення, коли вісь фази співпадає з осю q.

Взаємоіндуктивності фаз статора з обмотками ротора теж є складні функції (періодичні) кута . Тому що роторні обмотки f i D рухаються відносно обмоток статора. Максимальні значення мають місце також тоді осі фаз f i D співпадають з осями А (або В; С).

Тобто М_Af=M_AfdCos. (Тут M_Afd максимум M_Af, коли осі фаз f та А співпадають, тобто d та А одна лінія). Аналогічно:

Для взаємоіндуктивностей фаз А; В; С з обмоткою Dd записуються аналогічні вирази: (для осі d)

М_Аd=M_ADdCos (тут M_Addмаксимум M_AD, співпадають осі А і D);

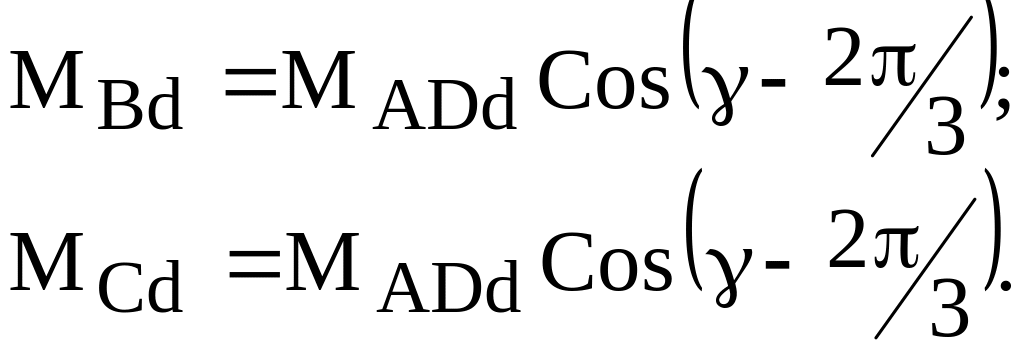
Для осі q:

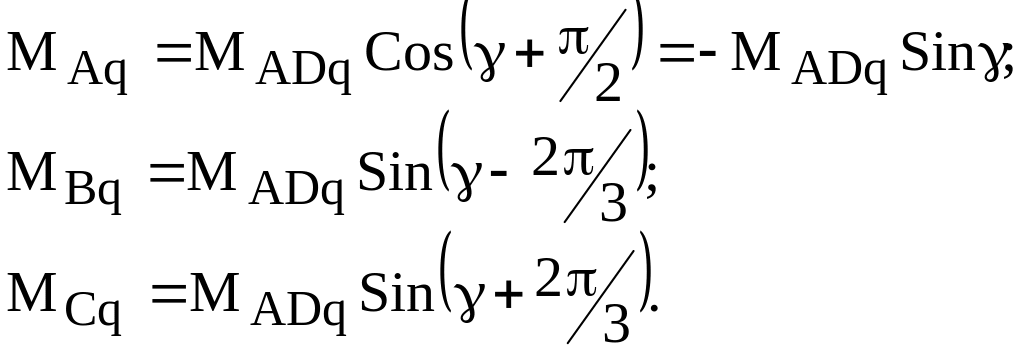
Коефіцієнти взаємоіндукції фаз статора з іншими обмотками статора також є складні функції кута обертання ротора  [ ].

Максимуми взаємоіндуктивностей між фазами статора мають місце коли осі А і d співпадають вони позначаються: Мінімуми цих величин мають місце коли співпадають осі q і А:

Взаємоіндукція між обмоткою збудження f, та демпферною осю d буде константа, тому що _d=const, а саме М_fDd=const.

Взаємоіндукція між обмоткою Dd з обмоткою f, та обмоткою Dd відсутня (тобто 0), тому що осі d і q мають кут 90⁰ел.

Якщо тепер підставити вирази для індуктивностей та взаємоіндуктивностей в рівняння для потокозчеплень фаз статора (А; В; С) та ротора (f; Dd; Dq), то будемо мати (напр. для фази А):

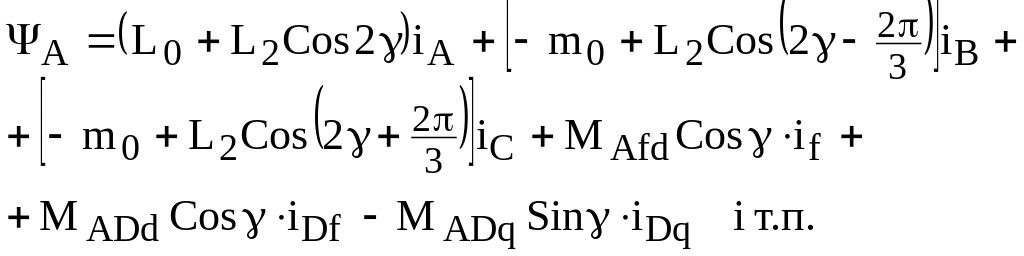
Якщо одержані вирази потокозчеплень фаз статора і ротора підставити в рівняння електричної рівноваги контурів статора і ротора, то отримаємо систему ДР з дуже складними нелінійними коефіцієнтами, яка може бути вирішена тільки чисельними методами.

Щоб позбутися періодичних коефіцієнтів (косинусних функцій кута ) в СДР СМ для реальних фазних величин треба виконати лінійні перетворення рівнянь.

Як відомо з теорії [1,2] СДР буде мати тільки тоді постійні коефіцієнти, коли магнітні осі фаз статора і ротора будуть взаємонерухомі одні відносно других. Це означає. Що треба дійсні змінні реальної СМ (напруги, струми, потокозчеплення і т.п.) замінити новими. Найпростіше така заміна здійснюється методом перетворень координат. Змінні старої системи ДР (напр. і_А; і_В; і_С…) перетворюються в нові (і_d; i_q;i₀)/

Загальне правило таке: змінні в системі нових осей (d; q) знаходяться як сума проекцій складових і_А; і_В; і_С на ці осі, тобто:

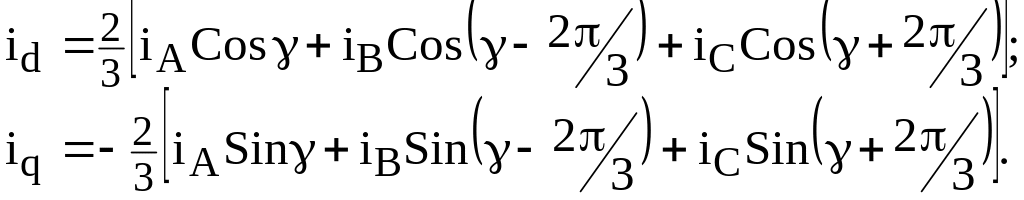
Якщо є потреба мати реальні струми фаз, знаючи складові і_d та i_q, використовують формули зворотнього перетворення; (за тим же загальним правилом)

Особливості струму і₀ (нульової складової): він входить у всі фазні струми та, протікаючи по симетричній трифазній обмотці, не може створювати обертове магнітне поле взаємоіндукції. Крім того ці струми можуть протікати в фазах тільки тоді, коли є нульовий провід з мережею живлення.

Після перетворення всіх фазних величин реальної СМ (напруг, струмів та потокозчеплень) до координатної системи d; q рівняння рівноваги напруг фаз статора мають вигляд:

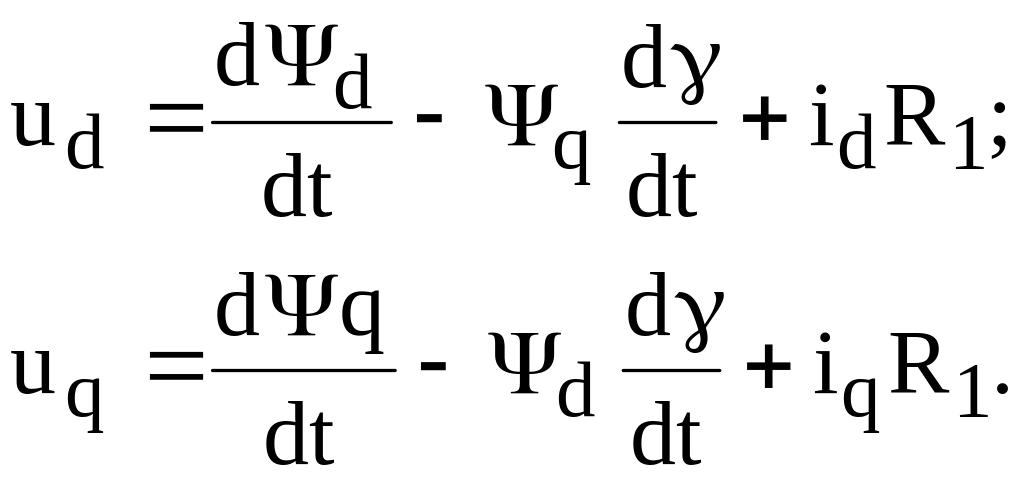
Роторні рівняння перетворенням не підлягають, тому що вони вже є записані в системі d; q .

Для того, щоб одержані рівняння можна було вирішувати, треба або всі потокозчеплення що входять в СДР виразити через струми, або навпаки.

Частіше за все записують потокозчеплення через струми (після перетворень та введення позначень)

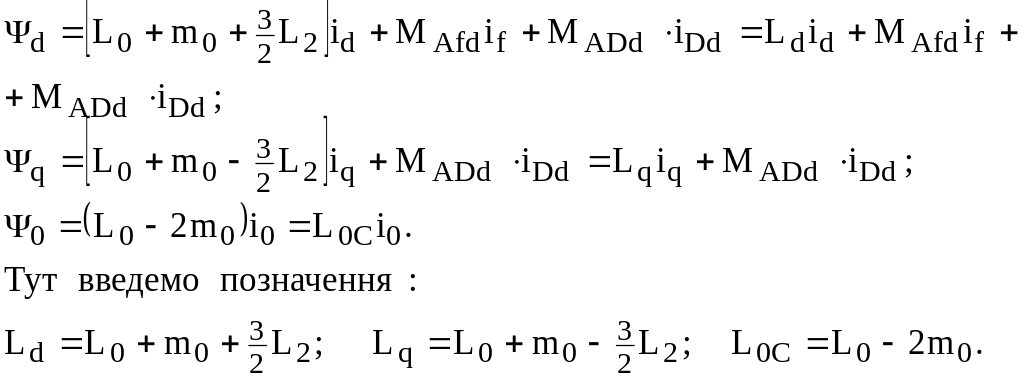
Повні індуктивності L_d; L_q; L_0C фаз статора d; q; 0, що визначають повні потокозчеплення в осях d; q, мають простий фізичний смисл: L_d – повна індуктивність фази статора (що має симетричну систему струмів) коли ротор рухається синхронно, а вісь поля співпадає з осю d; а опір Х_d=L_d – синхронна реактивність поздовжньої осі. Аналогічне пояснення і для інших індуктивностей.

Потокозчеплення роторних обмоток через і_d та і_q виражаються слідуючим чином:

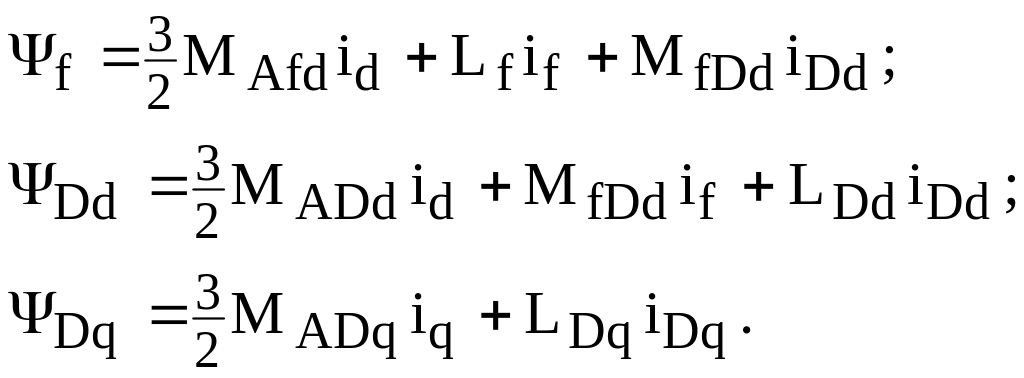
Якщо зважити на те, що , то повна СДР синхронної машини (система Парка-Горєва) має вид:

Аналогічний запис для СДР буде і в відносних одиницях. Тепер цю систему можна набирати як структуру в згідно з програмою SIAM на ПЕОМ.