35

Міністерство освіти і науки України

Дніпродзержинський державний технічний університет

МЕТОДИЧНІ ВКАЗІВКИ

до лабораторних робіт з курсу «Моделювання

електромеханічних перетворювачів”

для студентів спеціальностей 7. 092203 “Електромеханічні

системи автоматизації та електропривод” та 7. 092201 “Електричні системи і комплекси транспортних засобів”

Затверджено редакційно-видавничою секцією науково-методичної заради ДДТУ

_______________2008 р., протокол №

Дніпродзержинськ

2008

Методичні вказівки до лабораторних робіт з курсу «Моделювання електромеханічних перетворювачів” для студентів спеціальностей 7.092203 “Електромеханічні системи автоматизації та електропривод” та 7.092201 “Електричні системи і комплекси транспортних засобів”/ Укл.: к.т.н., доцент Сторожко С.П. - Дніпродзержинськ: ДДТУ,2005, 35 стор.

Укладачі: к.т.н., доцент Сторожко С.П.

Рецензент к.т.н., доцент Количев С.В.

Відповідальний за випуск: зав.кафедрою ЕО д.т.зв., професор Садовой О.В.

Затверджено на засіданні кафедри ЕО

(протокол № 1 від 3.09.2008 р.)

Методичні вказівки складаються з 2-х частин: теоретичної та практичної. В першій висвітлені деякі питання теорії математичного моделювання машин постійного та змінного струмів. В другій – наведені практичні вимоги з виконання відповідних лабораторних робіт з курсу “Математичне моделювання електромеханічних систем”.

З М І С Т

	стор.
ВСТУП………………………………………………………………..	4
1 ТЕОРЕТИЧНІ ЗАСАДИ МОДЕЛЮВАННЯ ЕМС……………….. 1.1 Математичне моделювання двигунів постійного струму (ДПС)	5 5
1.2 Моделювання ДПС при регулюванні потоку………………….	8
1.3 Математичне моделювання асинхронних двигунів……………	10
1.4 Практичні рівняння математичних моделей АД………………	13
1.5 Структурна схема математичної моделі узагальненої машини	16
1.6 Теоретичні особливості СДР синхронних двигунів (СД)…..	18
2 ЛАБОРАТОРНІ РОБОТИ……………………………………………………… 2.1 Лабораторна робота №1 “Моделювання двигуна постійного струму (ДПС) послідовного збудження”……………………………	25 25
2.2 Лабораторна робота №2. “Моделювання асинхронного двигуна (АД) (система ,)”…………………………………………	27
2.3 Лабораторна робота №3 “Моделювання асинхронного двигуна в осях х,у,0 (к=с)”……………………………………	28
2.4 Лабораторна робота №4. “Моделювання двигуна постійного струму (ДПС) (паралельне збудження)”……………………………	30
2.5 Лабораторна робота №5. “Моделювання асинхронного двигуна в осях dq (Wk=)”…………………………………………	32
2.6 Лабораторна робота №6. “Моделювання синхронного двигуна (СД)”…………………………………………………………	33
СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ…………………………..	34

ВСТУП

З метою виконання (наближених до реальних електромагнітних та електромеханічних перехідних процесів) розрахунків, а також визначення максимальних величин в електроприводі змінного та постійного струмів створюють математичні моделі електромеханічних систем (ЕМС).

Для одержання математичної моделі необхідно записати систему диференційних рівнянь (СДР), що описують поведінку ЕМС в любому режимі. Відомо, що [1] опис об’єкта регулювання в вигляді СДР є найбільш загальним, тому, що як частинний випадок, з нього можна одержати рівняння статичних режимів.

Математична модель електричної машини (ЕМ) любого типу складається на підставі рівнянь електричної рівноваги всіх контурів машини ЕМ, а також рівняння руху ротора (рівняння Даламбера).

Зв’язок між цими двома принципово різними фізично явищами встановлюється за допомогою рівняння закону електромагнітної енергії.

Кількість рівнянь СДР залежить від кількості фаз (обмоток) як статора так і ротора.

Складність математичної моделі визначається саме кількістю рівнянь СДР, тому часто цю систему перетворюють з метою спрощення як запису її, так і математичної моделі (ММ). Крім того існує дві форми запису СДР – відносно потокозчеплень. Або відносно струмів реальних фаз (або перетвореної ЕМ).

Тому потрібно також мати аналітичний зв’язок між потокозчепленнями фаз та струмами всіх фаз статора і ротора.

1 Теоретичні засади моделювання емс

1.1 Математичне моделювання двигунів постійного струму (дпс)

а) паралельне збудження

Як уже відмічалось, математична модель являє собою систему (СДР). Яка записується для фаз машини на підставі постулату про електричну рівновагу любого контура ЕМ (друге рівняння Кірхгофа). Запис рівняння другого закону Кірхгофа складається для відомої електричної схеми. На якій нанесені умовно позитивні напрямки всіх електричних величин (напруг, струмів, ЕРС).

Принципова схема ДПС рис.1.1 дає можливість скласти ДУ рівноваги електричного стану обмотки ротора (якоря).

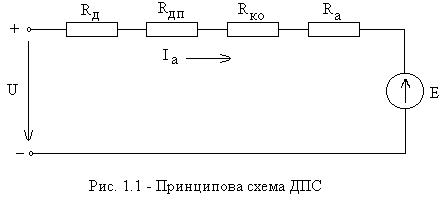
ЕРС обмотки якоря Е=КФ, тут К – коефіцієнт ЕМ,  - основний потік зазора ЕМ,  - миттєве значення кутової швидкості обертання.

В загальному випадку Фconst і залежить від струму збудження. Але навіть коли І_зб=const, потік міняється із-за впливу реакції якоря.

В загалі потік =Ф_о-_р.я., причому _р.я.=f(І_а) то при моделюванні ДПС з регулюємим потоком виникає необхідність врахування динамічних властивостей обмотки збудження (ОЗ) та нелінійності потоку від струму збудження.

Для машин постійного струму крива намагнічування задається вигляді універсальних кривих у відносних одиницях, або ж її можна задавати апроксимаційною кривою.

Припущення при складанні рівнянь:

1. Струм збудження має визначені значення.

2. Нехтуємо насиченням (не завжди) як по шляху основного потоку, так і розсіювання.

3. Не враховуємо вплив контура вихрових струмів.

4. Машина повністю скомпенсована, тобто відсутній вплив реакції якоря.

5. Комутаційна реакція якоря також не враховується.

За таких припущень вважається, що всі параметри схеми (рис.1.1) постійні, а також кФ=const.

Рівняння динамічної електричної рівноваги контура (рис.1.1):

Рівняння руху (форма Коші)

тут - знакова функція М_ст.

В канонічному вигляді

В операторному вигляді:

Якщо ДПС вмикається в систему автоматичного керування то його структурна схема буде працювати в загальній структурній схемі регуляторів та інших елементів, які складають електромеханічну систему (ЕМС).

б) послідовне збудження

Розглянемо СДР та структурну схему математичної моделі ДПС з послідовним збудженням для якого =f(I_a), причому ця залежність нелінійна.

Для цього випадку система ДР має вигляд:

В математичну модель добавлене ще одне рівняння (алгебраїчне нелінійне без врахування гістерезісу).

С труктурна схема моделі виглядає: (рис.1.3)

Рисунок 1.3 – Структура ДСП з послідовним збудженням

1.2 Моделювання дпс при регулюванні потоку

Розглянемо особливості моделювання ДПС, якщо струм збудження регулюється.

Обмотка збудження в цьому випадку в перехідних режимах представлена двома параметрами R_f; L_f. За умови реакції якоря, що скомпенсована у всіх режимах маємо рівняння електричної рівноваги обмотки збудження (ОЗ)

Як видно зрівняння (після відомих з ТАУ) перетворень обмотка (ОЗ) зображається апериодичною ланкою виду

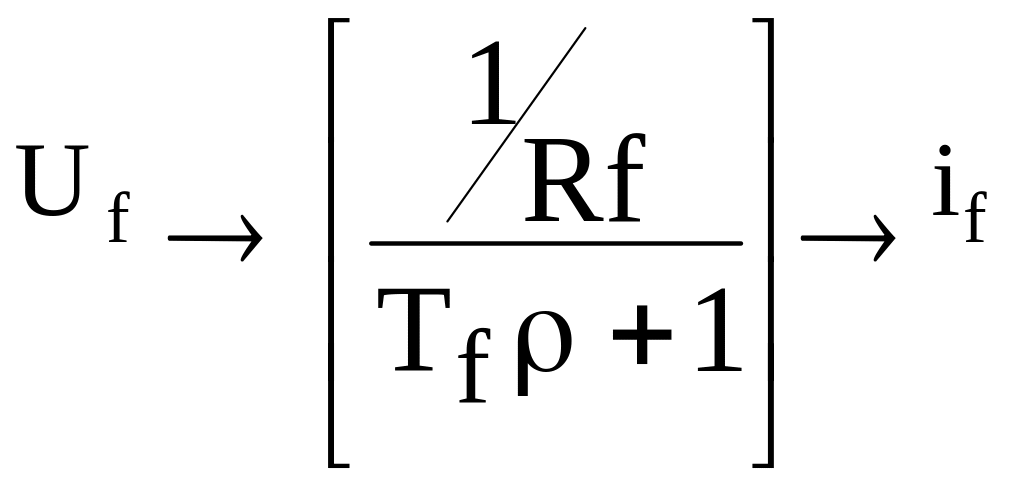
Рисунок 1.4 – Ланка збудження

Магнітний потік змінюється у відповідності з кривою намагнічування =f(і_f).

Система ДР при регулюванні має вигляд:

к =f(і_f)

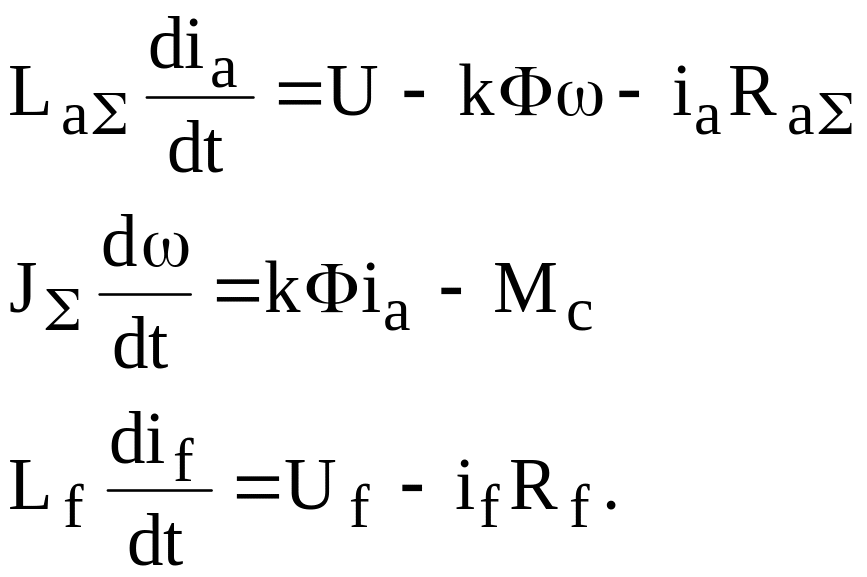
Після перетворень в операторному вигляді структурна схема ДПС з регулюванням струму збудження (друга зона) рис.1.5.

Рисунок 1.5 –Структура ДПС з регулюванням потоку