Зв’язок параметрів еквівалентної заступної схеми асинхронного двигуна з коефіцієнтами диференційних рівнянь:

L₁,L₂,M₁,M₂,M₁₂

Для аналітичного розрахунку перехідного процесу треба знати числові величини всіх коефіцієнтів диференційного рівняння, індуктивностей та взаємоіндуктивностей. В довідниках по АД можна знайти параметри еквівалентної заступної схеми (Т-подібна або Г-подібна уточнена).

Звичайні параметри Т-подібної схеми є: x₁,x₂,R₁,R₂,x_m.

x₂ – зведений параметр роторної обмотки

R₁,R₂ – активні опори (R₂-зведений) фаз статора і ротора

Для встановлення зв’язку між параметрами Т-схеми та коефіцієнтами систем слід записати диференційне рівняння в усталеному режимі, та порівняти їх з аналітичними виразами, які звичайно використовуються в загальній теорії електричних машин.

Для складання такої системи запишемо функціональні залежності в часі струмів статора і ротора за умови довільного значення початкової фази.

де: І_м1(І_м2) – амплітуди струмів статора (ротора)

() – початкові фази струмів статора (ротора)

Усталене значення напруги статора (без ротора):

U_A=U_M1sin(₀t+)

U_B=U_M1sin(₀t+-120^o)

U_C=U_M1sin(₀t++120^o)

Роторні напруги дорівнюють нулю.

_А=-

Рис.

В зв’язку з тим, що при перетворенні координат реальної машини в модельну, миттєві значення змінних знаходяться як проекції зображуючих векторів на відповідні координатні осі. Кожна проекція є косинусна функція прилеглого кута між зображуючим вектором і відповідною віссю. Тому будемо вважати, що усталені значення струмів та напруг АД теж записані через косинус , при цьому будемо вважати, що їх початкові фази такі самі, як і для синусних величин. Тому підставимо значення струмів статора і ротора в рівняння потокозчеплень, враховуючи функції cos та =t . Будемо мати:

_А=I_m1 [L₁cos(₀t+)+М₁cos(₀t+-120^o)+М₁cos(₀t++120^o)]+

+I_m2[M₁₂ costcos[(₀ -)t+]+M₁₂ cos(t+120^o)cos[(₀ -)t+

+-120^o]+M₁₂ cos(t-120^o)cos[(₀ -)t++120^o]]

Виконаємо перетворення гармонічних функцій, що входять в рівняння згідно з формулами тригонометрії:

Cos(+)=coscos-sinsin

Cos(-)=coscos+sinsin

Для статора:

=(t+), =120^o

Для ротора:

=[(₀-)t+]

Перетворимо вираз для струму I_m1:

L₁cos(₀t+)+М₁cos(₀t+-120^o)+М₁cos(₀t++120^o)= L₁cos+

+М₁cos(-)+М₁cos(+)=L₁cos(₀t+)+М₁[cos(₀t+)cos120^o+

+sin(₀t+)sin120^o]+М₁[cos(₀t+)cos120^o-sin(₀t+)sin120^o]=

=L₁cos(₀t+)+М₁[cos(₀t+)(-0,5)+sin(₀t+) ]+М₁[cos(₀t+

+)(-0,5)-sin(₀t+) ]= (L₁-М₁)cos(₀t+)

Перетворимо вираз біля струму I_m2:

M₁₂ costcos[(₀ -)t+]+M₁₂ cos(t+120^o)cos[(₀ -)t+-120^o]+

+M₁₂ cos(t-120^o)cos[(₀ -)t++120^o]=M₁₂ coscos+

+M₁₂ cos(+)cos( -)+M₁₂ cos(-)cos( +)=M₁₂ coscos+

+M₁₂ [coscos120^o-sinsin120^o][coscos-sinsin]+

+M₁₂ [coscos-sinsin][coscos-sinsin]= M₁₂ cos(₀ t+)

Для потокозчеплення _А маємо вираз:

_А=I_m1[(L₁-M₁)cos(₀ t+)]+I_m2[ M₁₂cos(₀ t+)]

Виконаємо аналогічне перетворення для ротора, в результаті будемо мати:

_а=I_m2[(L₁-M₁)cos[(₀ -)t+]]+I_m1[ M₁₂cos[(₀-) t+]]

Перейдемо до комплексного виду запису рівняння електричної рівноваги. Для виразимо миттєві значення через комплексні амплітуди та оператори обертання зображуючого вектора.

U_A=U_me^{(t+)}

i_A=I_m1e^{(t+)}

i_a=I_m2e^{[(-)t+)}

Підставимо миттєві значення в рівняння електричної рівноваги фази. Будемо мати:

U_A=І_m1e^{(t+)}R_A+

U_me^{(t+)}=І_m1e^{(t+)}R_A+

Запишемо потокозчеплення фази А в комплексному вигляді:

_А=(L₁-M₁)I_m1e^{(t+)}+ I_m2M₁₂e^{(t+)}

Знайдемо похідну

=j₀(L₁-M₁)I_m1e^{(t+)}+j₀ I_m2M₁₂e^{(t+)}

Введемо комплексні амплітуди для струмів статора і ротора:

I_m1=I_m1e^j

I_m2=I_m2e^j

Підставимо комплексні амплітуди струмів:

=j₀(L₁-M₁)I_m1e^t+j₀ I_m2M₁₂e^t

Підставимо значення похідної в рівняння електричної рівноваги в комплексному вигляді, будемо мати:

= R_A+[j₀(L₁-M₁)I_m1e^t+j₀ I_m2M₁₂e^t]

Перетворимо одержаний вираз таким чином:

= R_A+j₀(L₁-M₁)I_m1+j₀ I_m2M₁₂+j_{0 m1}M₁₂-j₀ I_m1M₁₂

Згрупуємо подібні члени:

= R_A+j[₀(L₁-M₁)-₀ M₁₂ ]I_m1+j₀ M₁₂( _m1+ _m2)

Введемо позначення:

x₁=₀(L₁-M₁)-₀ M₁₂

x_m= M₁₂₀

Підставляємо введені параметри і ділимо праву і ліву частини на :

= ₁(R₁+jx₁)+jx_m( ₁+ ₂)

В загальній теорії електричних машин відомо, що струм холостого хода :

( ₁+ ₂)= ₀

Тоді маємо:

= ₁(R₁+jx₁)+jx_{m 0}

Для ілюстрації зв’язку між параметрами еквівалентної заступної схеми :

=- ₁+j ₁x₁+ ₁R₁

=j₀[(L₁-M₁) ₁- M_{12 1}]- ₁R₁- j₀ M_{12 10}

Розглянемо еквівалентну Т-подібну заступну схему :

Рис.

R_нав=R₂

(R₂ +R_нав)=

x_m=j₀ M₁₂

x₁=x_S-x_m

x_S=x₁+x_m

З виразу для х₁ видно, що x₁=x_S-x_m або x_S=x₁+x_m

x_S – синхронна реактивність фази статора коли ротор рухається зі швидкістю поля.

Для ротора виконаємо аналогічні перетворення як і для статора. Тобто запишемо рівняння електричної рівноваги в комплексному вигляді для усталеного режиму.

U_а=і_аR₂+ =0

Вважаємо, що:

І₂= e^j

Це рівняння буде мати вигляд:

0=j(₀ -)(L₁-M₁) _m2e^j +j(₀ -)( M_{12 m1}e^j )+

+ _m2R₂e^j )

Введемо комплекси діючих значень:

0=j(₀ -)(L₁-M₁) ₂+j(₀ -)( M_{12 1})+ ₂R₂)

Для того, щоб позбавитись від струму ₁ в рівнянні добавимо і віднімемо вираз: j(₀ -) M_{12 2}

0=j(₀ -)(L₁-M₁) ₂+j(₀ -) M_{12 2}+R₂I₂+ j(₀ -) M_{12 2}-

• -j(₀ -) M_{12 2}

Остаточно маємо:

j(₀ -)(L₁-M₁) ₂- j(₀ -) M_{12 2}+j(₀ -) M_{12 10}+R₂I₂

З Т-подібної схеми видно, що

Замінимо –Е₂ на - =jI₁₀x_m , та будемо мати:

-jI₁₀x_m

jI₁₀x_m

Для порівняння виразу з еквівалентної схеми з формулою через коефіцієнти L₂, M₂, M₁₂ введемо ковзання в це рівняння. Для цього помножимо кожну складову на ₀ і поділимо на ₀-. В результаті будемо мати:

j₀(L₂-M₂) ₂- j₀ M_{12 2}+j₀ M_{12 10}

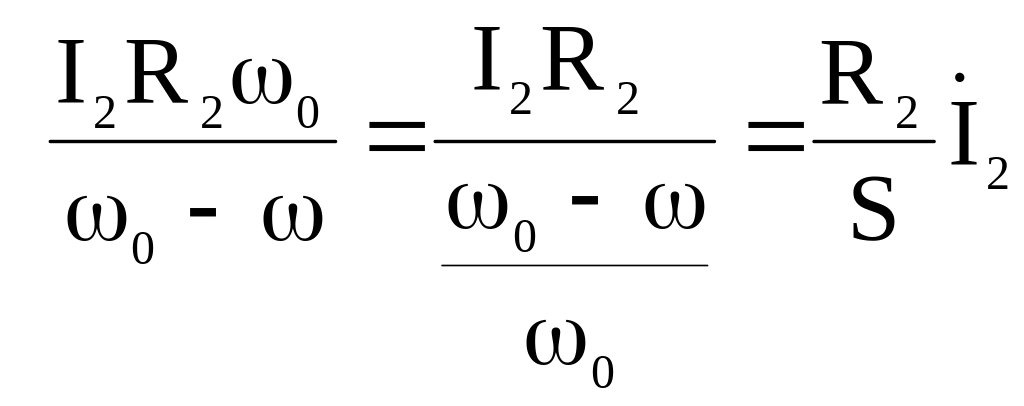
З порівняння одержаного виразу з формулою по еквівалентній заступній схемі видно, що:

jx₂=j₀(L₂-M₂) - j₀ M₁₂

x_m=j₀ M₁₂

Тепер ясно, що x₂=x_r-x_m, або x_r=x₂+x_m

де:

x_r – синхронна реактивність фаз обмотки ротора при живленні її напругою частоти ₀ коли ротор розімкнутий

Перетворення диференційних рівнянь машин.

Фізичний смисл перетворень складається в тім, що наявність періодичних коефіцієнтів рівнянь вимушує дослідників шукати шляхів спрощення рівнянь з метою запису їх з постійними коефіцієнтами. Для цього треба здійснити заміну змінних в рівнянні. Будемо вважати, що нова система диференційних рівнянь записана відносно нових змінних відображає ідеалізовану синхронну машину, у якої напруги, струми і потокозчеплення всіх фаз мають аналітичний зв’язок з реальними спеціальними формулами заміни змінних. Оскільки система рівнянь тепер не має періодичних коефіцієнтів, то фізично це означає, що ротор і статор цієї ідеалізованої машини є взаєморухомі тому, що змінні коефіцієнти в системі з’явились як результат руху роторних обмоток відносно статорних. Будемо вважати, що статор і ротор ідеалізованої машини обертаються в просторі з довільною частотою _к . При цьому конкретний вибір цієї частоти обертання може змінювати зовнішній вигляд рівнянь зпрощюючі, або ускладнюючі їх.

Припустимо також для спрощення системи, що ідеалізована машина є двофазна реальної трьохфазної машини за величиною ЕРС зазора створеними струмами статора і ротора. Схематично така двофазна машина має вигляд:

Рис.

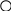
• ЕРС фази, яка враховує наявність обертання ротора відносно статора в реальній машині, а також враховується при цьому задана швидкість обертання _к координатних осей UV.

Напруги відповідних фаз мають індексацію відповідної осі обмотки. Всі електричні величини також прив’язуються до назви координатних осей. Цифровими індексами 1(2) позначаються статорні (роторні) величини.

Для перетворення системи диференційних рівнянь трьохфазної реальної машини вирішується 2 задачі:

1) необхідно знайти формули зміни старих змінних на нові,

2) використовуючи ці формули одержати систему диференційних рівнянь в нових змінних.

Для вирішення цих задач розглянемо рис.2, на якому показані координатні системи реальних фаз статора і ротора та координатна система ідеалізованої машини. Крім того, будемо вважати, що зображуючі вектори ЕРС статора і ротора представлені на цьому рисунку в вигляді струму ( вектора еквівалентного відповідній ЕРС ).

Рис.2

Як відомо з загальної теорії електричних машин миттєві значення струмів в реальних фазах машини визначаються як проекції зображуючого вектора струму статора (ротора) на координатні осі реальних фаз статора (А,В,С), ротора (а,в,с). Аналогічний висновок буде і для координатної системи UV.Струм i_u1 буде проекція струму І_і на координатну вісь U. А струм і_v1 є проекція цього ж вектора на вісь V.

Для ротора миттєві значення теж визначаються як проекції зображуючого вектора І₂ на координатні осі для відповідних фаз.

Якщо тепер виразимо аналітично миттєві значення струмів фаз як проекції зображуючого вектора, то ми можемо знайти необхідні формули зв’язку між старими змінними і новими змінними. Для того, щоб можна було записати аналітичні вирази для проекції струмів І_і та І₂ треба позначити величини кутів між зображуючим вектором та осями нерухомих та рухомих фаз. За точку відліку кутів приймаємо напрямок фази А статора.

Запишемо миттєві значення струмів фаз через відповідні проекції:

і_А=І₁cos₁

і _В=І₁cos(₁-120^)

і _С=І₁cos(₁+120^)

де ₁- кут між вектором І₁ та фазою А

І₁- модуль вектора

Аналогічно знайдемо вирази миттєвих значень струмів фаз еквівалентної машини, які носять назву U,V можна записати також як проекції вектора струму на координатні осі U і V.

і_u1= cos(_кt-₁)

і_V1=- sin(_кt-₁)

Тепер задача складається в тім, щоб із цих двох систем знайти вирази для струмів і_u1 та і_V1 в залежності від реальних струмів і_А, і_В, і_С, тобто , знайти формули перетворення реальної машини в еквівалентну двофазну. Розпишемо в першому рівнянні другої системи:

і_u1= cos(_кt-₁)= cos₁ cos_кt+ sin₁ sin_кt

З цього запису видно, що cos₁= і_А , а значення sin₁= ,останній вираз можна довести наступним чином: з ТОЕ відомо, що і_А+ і _В+ і _С=0

і _В- і _С= І₁cos(₁-120^)-І₁cos(₁+120^)

Якщо розкладемо cos різниці та суми двох кутів, то вважаючи на те, що і_А=-( і _В+і _С)= І₁cos₁, то після підстановки cos 120^та sin 120^ будемо мати вираз:

І₁cos₁= - І₁( cos₁- sin₁+ cos₁+ sin₁)

Після перетворень знайдемо, що:

sin₁=

Після підстановки значень в перше рівняння будемо мати:

і_u1= і_А сos _кt +  sin _кt

Останній вираз може бути перетворений :

і_u1= і_А сos _кt + і _Вcos(_кt -120^)+і _Сcos(_кt +120^)

Таким чином, для того, щоб записати струм фази U, вісь якої обертається в просторі з довільною швидкістю _к , треба знати струми реальних фаз та конкретне значення швидкості _к.

Виконаємо аналогічні перетворення для знаходження струму фази U статора (і_V1), який має такий вигляд:

і_V1= - і_А sin _кt + і _Вsin(_кt -120^)+і _Сsin(_кt +120^)

Таким чином, ми одержали формули прямого перетворення від реальних струмів машини до еквівалентних струмів двофазної ідеалізованої машини. Якщо машина буде m-фазна перетворюватись в двофазну, то коефіцієнт буде не 2/3, а 2/ m.

Розглянемо аналогічні перетворення реальних струмів ротора і_а , і_в , і_с в струми і_u2 та і_v2. Як видно з рисунку координатних систем лінії а, в, с позначають осі фазних обмоток ротора. Вектор струму є зображуючий вектор сумарної ЕРС ротора. Згідно з загальною теорією, вектор струму повинен бути в протифазі відносно струму так, щоб їх сума завжди дорівнювала намагнічуючому струмові:

+ = const.

Зв’язок між струмом та реальними струмами фаз запишемо як проекції струму і₂ на реальні фазні осі ротора.

В цих виразах:

₂ – кут між вектором віссю фази А статора

 - кут, миттєве значення положення ротора відносно статора =t.. Відраховується від осі а ротора в формулах перетворення.

Аналогічно як для статора виразимо струми двофазних обмоток ротора еквівалентної машини як проекції вектора на координатні осі U і V.

Тепер з останніх двох систем можна записати залежності і_u2(і_а,і_в,і_с) , і_v2(і_а,і_в,і_с). Для спрощення процедур приймаємо ₂ - =.

Розписуються аналогічно косинуси різниці та суми двох кутів (- 120^) та (- 120^). Після всіх перетворень, таких же, як і для статора, струми фаз ротора еквівалентної машини мають вигляд:

і_u2= і_а сos (_кt -)+ і _вcos( (_кt-) -120^)+і _сcos( (_кt-) +120^)

cos (_кt-t)= cos (_к-) t

і_V2= - і_а sin (_кt-) + і _вsin((_кt-) -120^)+і _сsin((_кt-) +120^)

Вирази для струмів статора, а також для струмів ротора в осях U і V, являють собою формули прямого перетворення, тобто формули перехода від реальних струмів двофазної машини.

Виникає питання чи досить двох нових змінних і_u1 , і_V1 для повної заміни трьох реальних струмів і_А , і_В , і_С, при переході до еквівалентної двофазної машини. Відповідь на поставлене питання можна одержати шляхом зворотнього перетворення, тобто шляхом визначення струмів фаз А, В, С реальної машини через струми еквівалентної машини. Для цього помножимо струм і_u1

1. і_u1cos_кt= cos_кtі_А сos _кt + і _Вcos(_кt -120^)+і _Сcos(_кt +120^)

Струм і_V1помножимо:

2. і_V1(- sin_кt)= sin _кt і_А sin _кt + і _Вsin(_кt -120^)+і _Сsin(_кt +120^)

Виконаємо відомі перетворення:

і_А сos² _кt + і _Вcos_кt (cos_кt cos 120^+sin_кt sin 120^)+ і _Сcos_кt(cos_кt cos 120^-sin_кt sin 120^)

Якщо з 1 рівняння визначимо струм фази А за допомогою його перетворень, то будемо мати:

і_А= і_u1cos_кt- і_u1 sin _кt+ (і_А +( і_В + і_С))

Введемо і_V1= (і_А +( і_В + і_С)) , де цей струм є струм нульового слідування фаз при розкладі несиметричної системи реальних струмів на симетричні складові: пряму, зворотню та нульову.

З останніх виразів видно, що струм і₀₁ не може бути виражений через і_u1 та і_V1. Це означає, що ні і₀₁, ні струми фаз А,В,С не можуть в загальному випадку бути записані через нові змінні, т.ч. для трьохфазної симетричної системи з нульовим проводом треба враховувати і₀₁, а для системи без нульового провода струм і₀₁=0, але в загальному випадку формули перетворення статорних величин мають 3 рівняння, тобто:

і_u1= і_А сos _кt + і _Вcos (_кt -120^)+і _Сcos(_кt+120^)

і_V1= - і_А sin _кt + і _Вsin(_кt -120^)+і _Сsin(_кt +120^)

і₀₁== (і_А + і_В + і_С)

Якщо виконати всі аналогічні процедури для ротора, то одержимо систему з трьох рівнянь для формул прямого та зворотного перетворень в загальному випадку( несиметрія ротора) будемо мати наступну систему:

1) і_u2= і_а сos (_кt -)+ і _вcos( (_кt-) -120^)+і _сcos( (_кt-) +120^)

2) і_V1= - і_а sin (_кt-) + і _вsin((_кt-) -120^)+і _сsin((_кt-) +120^)

3. і₀₂== (і_А + і_В + і_С)

Висновки:

1. Фізичний смисл формул перетворення для АМ в тім, що реальна трьохфазна машина зводиться до еквівалентної двофазної машини за величиною МРС, створеної струмами статора і ротора.

2. При цьому перетворенні завжди статор і ротор взаємно нерухомі і обертаються в просторі з довільною швидкістю _к.

3. Величина швидкості ротора відносно статора реальної машини та величина швидкості _к враховується додатковими ЕРС в фазах статора та ротора (е_u1, е_V1, е_u2, е_V2).

Оскільки любу трьохфазну систему напруг, струмів, ЕРС, або потокощеплень можна представити відповідними зображуючими векторами, то кожна з цих величин може бути перетворена з трьохфазної системи в двофазну згідно з формулами узагальненого перетворення. Ці формули мають вигляд:

f_u1(t)= f_A(t) сos _кt + f_B(t)cos(_кt-120^)+ f_C(t)cos(_кt+120^)

f_V1(t)= - f_A(t)sin _кt + f_B(t) sin (_кt-120^)+ f_C(t)sin (_кt+120^)

f_u2(t)= f_а(t) сos _кt + f_в(t)cos(_кt-120^)+ f_с(t)cos(_кt+120^)

f_V2(t)= - f_а(t)sin _кt + f_в(t)sin (_кt-120^)+ f_с(t)sin (_кt+120^)

Перетворення диференційних рівнянь асинхронної машини

Запишемо диференційне рівняння для потокозчеплень статора та ротора в нових координатах, тобто в системі осей, що обертаються з довільною швидкістю _к. Для цього _А множимо на сos _кt, рівняння для _В множимо на cos(_кt-120^), та рівняння для _С множимо на cos(_кt+120^)

_А сos _кt= L₁і_A сos _кt + M₁i _Вcos_кt+M₁і _Сcos_кt+ M₁₂cos_кt cos + +M₁₂i _вcos _кt cos(+120^o) + M₁₂i _сcos _кt cos(-120^o) 

_В сos(_кt-120^o)= М₁і_A сos(_кt-120^o) + L ₁i _Вcos(_кt-120^o)+M₁і _Сcos(_кt--120^o)+M₁₂cos(_кt-120^o)cos(-120^o)+M₁₂i _вcos(_кt- 120^o)cos+ +M₁₂i _сcos (_кt-120^o)cos(+120^o) 

_Ссos(_кt+120^o)= М₁і_Aсos(_кt+120^o)+М₁i_Вcos(_кt+120^o)+L₁і_Сcos(_кt+ +120^o)+M₁₂і_аcos(_кt+120^o)cos(-120^o)+M₁₂i_вcos(_кt+120^o)cos(-120^о)+M₁₂i _сcos (_кt+120^o)cos 

Якщо окремо складемо ліві частини рівнянь, то одержимо повне потокозчеплення фази U статора, а саме:

 _U1= _А сos _кt+_В сos(_кt-120^o)+ _Ссos(_кt+120^o) 

Праві частини будемо складати відповідно до членів з струмами фаз А,В,С статора та відповідними коефіцієнтами при цих струмах, які повинні бути однаковими. Записуємо окремо:

 L₁і_A сos _кt+L ₁i _Вcos(_кt-120^o)+ L₁і_Сcos(_кt+ +120^o) = L₁ і_u1

Виконаємо подібну операцію і для коефіцієнта М₁:

М₁(i_В+і_С)  сos _кt+(i_А+і_С) cos(_кt-120^o) +(i_А+і_В) cos(_кt+120^o) =- М₁ і_u1

i_А +i_В+і_С=0

i_В+і_С=- i_А

Виконаємо відповідну процедуру для коефіцієнта М₁₂:

М₁₂ і_аcos_кtcos+i _вcos _кt cos(+120^o)+i _сcos _кt cos(-120^o)+

+і_аcos(_кt-120^o)cos(-120^o)+i_вcos(_кt-120^o)cos+i_сcos(_кt-120^o)

cos(+120^o)+і_аcos(_кt+120^o)cos(+120^o)+i_вcos(_кt+120^o)cos(-120^о)+

+i _сcos (_кt+120^o)cos = М₁₂ і_u2

Згідно з формулами узагальненого перетворення та розкладання косинуса суми та різниці двох кутів та групування подібних членів одержимо М₁₂ і_u2

 _U1= L₁ і_u1- М₁ і_u1+ М₁₂ і_u2=( L₁- М₁) і_u1+ М₁₂ і_u2

Якщо виконати аналогічні перетворення по осі V статора, перемноживши потокозчеплення реальних фаз статора _А, _В, _С

 _V1= _Аsin _кt +_В sin (_кt-120^)+ _С sin (_кt+120^)

 _V1==( L₁- М₁) і _{V 1}+ М₁₂ і_V2

Перетворення роторних рівнянь

Якщо реальне потокозчеплення фаз ротора _а, _в, _с помножимо відповідно на сos_кt, сos(_кt-120^), сos(_кt+120^) і виконаємо аналогічні як для статора перетворення, то запишемо вирази для потокозчеплень фаз ротора еквівалентної двофазної машини по осям U та V.

 _U2=( L₂- М₂) і_u2+ М₁₂ і_u1

 _V2=( L₂- М₂) і _{V 2}+ М₁₂ і_V1

Якщо перемножимо праву і ліву частини кожного рівняння для потокозчеплення на ₀, то будемо мати:

₀ _U1=x_s і_u1 +x_m і_u2

₀ _V1= x_s і_V1 +x_m і_V2 (а)

₀ _U2= x_p і_u2+x_m і_u1

₀ _V2= x_p і _{V 2} +x_m і_V1

x_s (x_p) – синхронні реактивності статора (ротора) – знаходяться з еквівалентної заступної схеми.

x_m – реактивність взаємоіндукції між фазою статора і ротора - знаходяться з еквівалентної заступної схеми.