Тема 7 „СистемА – напівпровідниковий перетворювач – двигун постійного струму з підпорядкованим керуванням”

1. Принципи побудови систем підпорядкованого керування електроприводом

Переважна більшість сучасних СУЕП будуються за принципом підпорядкованого керування. Такі системи мають переваги у порівнянні з іншими (паралельної дії) в тому, що містять меншу кількість елементів; більш прості та зручні у налагоджувані. Систем підпорядкованого керування вводяться в експлуатацію методом послідовного настроювання окремих контурів, дозволяють легко вводити обмежуючі параметри та відносно просто здійснювати розрахунки системи.

Систем підпорядкованого керування будуються таким чином, щоб у кожній ланці в об’єкті в систему управління вводився регулятор, що контролює той чи інший параметр СУЕП. В якості активних коректуючих ланцюгів використовуються операційні підсилювачі (ОП) з різними передатними функціями. Передатна функція регулятора визначається структурою та параметрами відповідної ланки об’єкта управління, а також критерієм контура.

Найбільш частіше у електромеханічних системах контур регулювання кожного параметра має одну велику сталу часу, яка компенсується регулятором та декілька малих сталих часу. Оптимізацію системи можна розглянути на прикладі одноконтурної системи, яка має об’єкт з функцією аперіодично ланки з великою сталою часу та такою ж ланкою з малою сталою часу.

Передатна функція об’єкта (рис.1.4) буде

(7.1)

де К₀ – коефіцієнт підсилення об’єкта;

Т_ - сумарна мала сталого часу об’єкта;

Т – велика стала часу об’єкта.

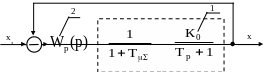
Рисунок 7.1 – Структурна схема системи регулювання:

1 – об’єкт регулювання;

2 – передатна функція регулятора

Передатна функція (7.1) має співмножник W_(p), яка відповідає ланцюгу , дії якої компенсується регулятором. В той же час, співмножник W_м(p) представляє собою добуток передатних функцій, еквівалентних періодичних ланок з малою постійною часу, дію яких не може бути скомпенсовано у силу їх фізичної природи, або компенсація недоцільна. [5]

З урахуванням прийнятих допущень, об’єкт регулювання можливо представити як одну аперіодичну ланку.

(7.2)

Очевидно, що для абсолютної компенсації такої ланки необхідно мати регулятор в системі керування у вигляді ідеального форсуючого ланцюга

(7.3) Фізично це означає, що для миттєвої зміни вихідної величини інерційної ланки на її вхід, необхідно подати імпульс напруги безмежної амплітуди, що неможливо. Тому у реальних системах, які мають обмежуючі можливості по управлінні, абсолютна компенсація неможлива. Але якщо прийняти безінерційний регулятор з великим коефіцієнтом підсилення, то при малих завданнях приросту вихідної величини можливо здійснити компенсацію близьку до оптимальної. Проте при такому підході, контур регулювання стає дуже чутливим до частотних перешкод, тому у тих випадках, коли об’єкт регулювання можливо представить аперіодичною ланкою, ступінь компенсації до абсолютної, обмежений границею, при якій смуга пропуску замкненого ланцюга забезпечує його захист від частотних перешкод. Останні умови можуть бути задоволені застосуванням пропорційно-інтегральним регулятором (ПІ-Р) з передатною функцією

(7.4)

де Кр – коефіцієнт підсилення регулятора.

З урахуванням попередніх міркувань, передатна функція розімкненої системи (рис.1.3) буде

(7.5)

Передатна функція замкненої системи

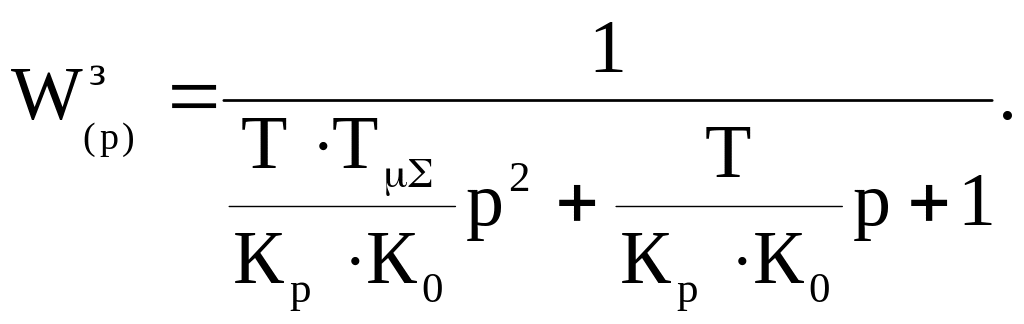(7.6)

Вираз (1.37) показує, що замкнений контур представляє собою систему другого порядку.

В залежності від коефіцієнтів вищої та нижчої похідної система носить коливальний, або аперіодичний характер. Для коливальної системи вираз (7.6) можна представити у більш зручній для аналізу формі [5]

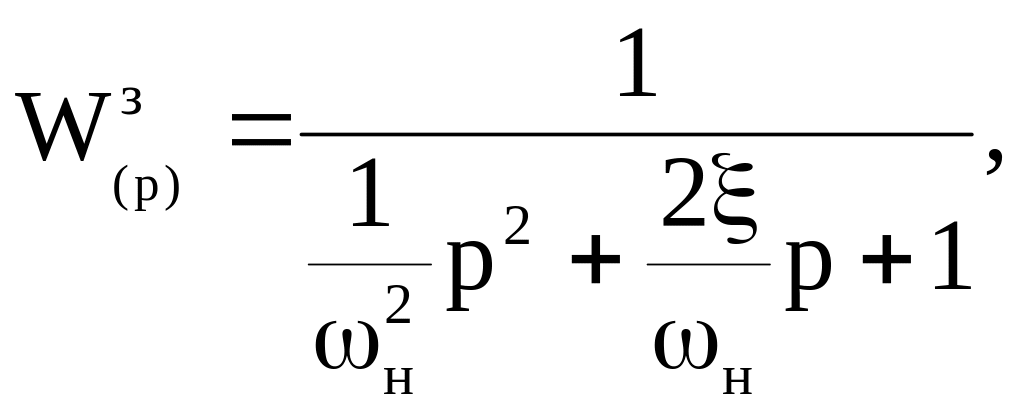(7.7)

де _н – частота недемфірованих коливань;

 - коефіцієнт демфірування.

Характер передатної функції системи у більшості залежить від коефіцієнта . Коли >1, то система аперіодична, а якщо <1 – коливальна.

Перехідні функції регулюючої величини на виході системи другого порядку при скачкоподібній зміні вхідного сигналу, при різних значеннях , мають вигляд (рис.1.5) [5]:

Як видно з графіків (рис.7.2) вихідні величини системи другого порядку представляють собою сімейство кривих у відповідності до різних значень коефіцієнта . У випадку оптимізації по Betrags–оптимум коефіцієнт  дорівнює [5]:

(7.8)

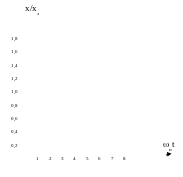
Рисунок 4.2 – Характеристики перехідної функції системи

другого порядку (₁=0,1; ₃=0,3; ₅=0,5; ₇=0,707)

Така перехідна функція характеризується величиною перерегулювання =4,3% та часом першого досягнення сталого режиму t_с=4,7Т_. Таке налагоджування контура є компромісом між великим перерегулюванням та швидкодією і здебільшого задовольняє електромеханічні системи. У вітчизняній літературі такий критерій оптимізації отримав назву технічного, або модульного (ТО).

Вирази (7.6) та (7.8) описують одну і ту ж систему другого порядку. На цій підставі коефіцієнти при вищій та нижній похідній можна прирівняти.

(7.9)

Це дає змогу отримати значення коефіцієнта демпфірування для систем (рис.1.3).

(7.10)

Підставивши значення =0,707= можна отримати коефіцієнт підсилення ОП, який дає змогу здійснити налагодження контура по технічному оптимуму.

(7.11)

Одержаний коефіцієнт (7.11) підставивши у вираз (7.4) отримаємо передатну функцію ПИ-регулятора.

(7.12)

аналіз виразу (7.12) дозволяє сформулювати наступні загальні правила вибору регулятора з оптимальним налагодженням:

1. кожній ланці з великою сталою часу у об’єкті повинна відповідати ланка із зворотньою передатною функцією і з тією ж сталою часу в системі регулятора;

2. величина В₀=2Т_, для внутрішнього контуру вибирається у відповідності до виразу (1.43), а для наступного контура подвоюється.