1.4. Движущая сила массообменных процессов.

Движущую силу массообменных процессов можно выразить через концентрации распределяемого вещества либо в фазе G, т.е. через Y, либо в фазе L через X.

Графически это может быть представлено четырьмя различными способами.

Во всех случаях движущей силой будет разность между рабочей и равновесной концентрацией, взятая с положительным знаком.

Основное уравнение массопередачи можно записать двояко:

Из графиков движущей силы следует, что последняя меняется с изменением рабочих концентраций, потому для всего процесса должна быть определена величина средней движущей силы.

Здесь могут встретиться два случая: 1) зависимость между равновесными концентрациями не линейна: Y_p =f(X); 2) зависимость между равновесными концентрациями линейна: Y_p =А_pX, где А_р — постоянная величина. 

При взаимодействии фаз концентрация Y уменьшается, а Х увеличивается (рис. 3). 

Основное уравнение массопередачи можно записать так:

где ΔY_m и ΔX_т – движущая сила процесса.

Отсюда площадь взаимодействия фаз

В этом уравнении величины

m_y и m_y – величины, показывающие, на сколько единиц изменяет рабочую концентрацию единица движущей силы, называется числами переноса.

Для элемента поверхности имеем:

dM = K_y(Y - Y_p)dF и dM = G(-dY), откуда:

После интегрирования от 0 до F и от У_н до У_к имеем:

Если выразить движущую силу через X, то получим:

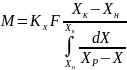
Сопоставив эти уравнения с (14), найдем выражения для средней движущей силы:

Практически знаменатели дробей находят графически интег­рированием. Для эксперимента находят значения Y, Y_p и вычисляют значения 1/У- У_р. Затем в координатах (1/У- У_р), Y строят кривую.

Рис. 4. Графическое выражение числа переноса

Площадь под этой кривой, ограниченная ординатами Y_K и У_н умноженная на масштаб диаграммы а, дает искомый интеграл

Так же поступают при нахождении знаменателей дроби, при выражении движущей силы через концентрацию X. Дроби в уравнениях (17) и (18) имеют физический смысл чисел переноса.

Для случая линейной зависимости между равновесными концентрациями аналогичными рассуждениями найдем, при условии, что Y = AX и Y_P = A_PX,

После ряда преобразований, выразив А через Y и X, соответ­ственно получим:

1.5. Основные законы массопередачи.

1.5.1. Разновидности массообмена.

В процессах переноса вещества из одной фазы в другую следует различать два случая:

1 . Массообмен между потоками жидкостей (жидкость -жидкость, газ - газ, жидкость - газ, газ - жидкость).

2. Массообмен между твердым телом и потоком жидкости (твердое тело - жидкость (газ), жидкость (газ) - твердое тело).

Элементарными законами, которым подчиняется перенос вещества из фазы в фазу, являются законы:

- молекулярной диффузии,

- массоотдачи,

- массопроводности.

1.5.2. Закон молекулярной диффузии (первый закон Фика).

Формулировки первого закона Фика и закона теплопроводности аналогичны: количество продиффундировавшего вещества пропорционально градиенту концентраций, площади, перпендикулярно направлению диффузионного потока и времени.

Этот закон справедлив в том случае, когда происходит хаоти­ческое движение молекул в неподвижной жидкости при малых концентрациях растворенного вещества.

Записывается этот закон следующим образом:

где dM - количество продиффундировавшего вещества, дс/дп -градиент концентрации в направлении диффузии, D- коэффициент диффузии.

Коэффициент диффузии D показывает, какое количество веще­ства продиффундирует через поверхность 1 м² в течение одного часа при разности концентраций на расстоянии 1 м, равной единице.

Размерность коэффициента диффузии зависит от способа выражения концентрации.

Если принять, что [М] = [кг], [F] = [м²], [τ] = [с], [С] = [кг/м³],[n] = [м],то

Коэффициент диффузии не является постоянной величиной; он зависит от температуры, давления, концентрации веществ, мо­лекулярного веса взаимодействующих веществ, вязкости жид­кости, в которой происходит диффузия. Находят его либо вычислением по эмпирическим формулам, либо по справочным таблицам.

Для газов D на четыре порядка выше, чем для капельных жидкостей.

1.5.3. Дифференциальное уравнение молекулярной диффузии (второй закон Фика).

Если рассмотреть перемещение распределяемого вещества за счет диффузии в элементарном объеме в координатах х, у, z, то аналогично случаю с потоком жидкости получим:

Изменение концентрации вдоль оси Х:

вдоль оси У:

вдоль оси Z:

для всего объема dV:

С другой стороны, это же количество вещества можно найти, умножив объем dV= dxdydz нa изменение концентрации за время dτ, если за единицу времени это изменение составит дС/дτ.

Приравнивая (24) к (25), получим:

или

(уравнение, аналогичное уравнению теплопереноса).

6.5.4. Закон массоотдачи (закон Щукарева).

Этот закон аналогичен закону охлаждения Ньютона и формули­руется так: количество вещества, перенесенного от поверхности раздела фаз в воспринимающую фазу, пропорционально разности концентраций у поверхности раздела фаз и в ядре потока восприни­мающей фазы, поверхности фазового контакта и времени.

где β - коэффициент массоотдачи, характеризующий перенос вещества диффузией и конвективным переносом одновременно; С_r — концентрация у поверхности раздела фаз в воспринимающей фазе; С_ф - концентрация в ядре потока воспринимающей фазы.

Здесь С_г рассматривается как равновесная концентрация.

Размерность при выражении концентрации в кг/м³

показывает, какое количество вещества передается в восприни­мающую фазу от поверхности раздела фаз через 1 м² фазового контакта за 1ч при разности концентраций 1 кг/м³.

Для установившегося процесса значение β постоянно, т.е. не изменяется во времени, поэтому для такого процесса можно написать:

Для конкретных расчетов можно принять:

или

1.5.5. Дифференциальное уравнение массоотдачи (уравнение конвективной диффузии).

В основу рассмотрения явлений конвективной диффузии поло­жена теория диффузионного граничного слоя, которую разделяют большинство ученых.

Согласно этой теории распределяемое вещество переносится из ядра потока к границе раздела фаз и потоками жидкости, и молеку­лярной диффузией. В этом случае воспринимающая фаза должна быть либо твердой, либо способной гасить турбулентные пуль­сации почти как твердое вещество. В такой системе поток можно рассматривать как состоящий из ядра и граничного диффу­зионного слоя (снова аналогия с теплопереносом).

В ядре потока перенос вещества происходит за счет турбулент­ного перемешивания жидкости; при достаточно развитой турбулентности концентрация распределяемого вещества в ядре потока усредняется и может считаться постоянной.

По мере приближения к граничному диффузионному слою турбулентный перенос затухает и начинает преобладать перенос за счет молекулярной диффузии. Появляется градиент концент­рации, растущей по мере приближения к границе (стенке). Область появления и роста градиента концентрации и представ­ляет собой граничный диффузионный слой.

Здесь молекулярная диффузия увеличивается от ничтожного значения до максимального. Для элементарного объема, перемещающегося в граничном диффузионном слое, концентра­ция становится не только функцией координат и времени, но и функцией скорости потока. Поэтому изменение можно выразить через субстанциональную производную:

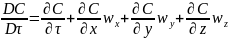
Приращение массы вещества в элементарном объеме через субстанциональную производную выразится как

Но в то же время

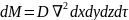
Поэтому

Это уравнение является дифференциальным уравнением конвективной диффузии.

1.5.6. Критериальное уравнение конвективной диффузии.

Уравнение (32) необходимо дополнить уравнением, характе­ризующим граничные условия. Это уравнение массоотдачи:

Обозначив (С_r - С_ф) = ΔС, запишем:

То же количество вещества можно определить при помощи уравнения молекулярной диффузии:

Приравнивая правые части, получим:

Преобразуя (33) по теории подобия, получим безразмерный комплекс:

Заменив здесь n линейным размером l и вычеркнув символы математических операторов, получим критерий Шервуда Sh (по прежней терминологии - диффузионный критерий Нуссельта Nu_д):

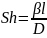
Из дифференциального уравнения конвективной диффузии:

Получим:

Разделив обе части на правую, имеем:

Здесь

Ре_д преобразуем, разделив и умножив его на кинематичес­кую вязкость:

где Sc - критерий Шмидта или по старой терминологии диффузионный критерий Прандтля Рг_д

Если процесс протекает в условиях свободной конвекции, вызванной различной плотностью растворов разной концентра­ции, вводят вместо Re или дополнительно к нему критерий Грасгофа:

Критериальное уравнение конвективной диффузии таково:

Здесь определяемым является критерий Шервуда, т. к. он один не состоит целиком из условий однозначности (начальных и граничных условий):

В конкретных случаях условие (35) может быть упрощено. При стационарном массообмене выпадает критерий Фурье, характеризующий изменения системы во времени.

Тогда

При вынужденном движении можно пренебречь естественной конвекцией, поэтому выпадает критерий Грасгофа:

При свободной конвекции становится не нужным критерий Рейнольдса:

или

Конкретные формы функциональной зависимости между критериями подобия устанавливают экспериментально или находят в справочной литературе. По найденным значениям Sh находят коэффициент массоотдачи: