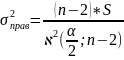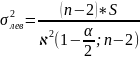- •Вариант 2
- •Алгоритм решения задачи
- •Решение
- •Рассчитаем средние арифметические и
- •Определим дисперсию
- •Рассчитаем среднее квадратическое отклонение
- •Определим коэффициент регрессии b
- •Рассчитаем коэффициент корреляции
- •Определим стандартную ошибку коэффициента корелляции
- •Рассчитаем t-критерий Стьюдента
- •Определим доверительный интервал для коэффициента корелляции
- •Определим параметры для расчета корреляционно-регрессионного уравнения
- •Рассчитаем теоретическое значение
- •Алгоритм решения задачи
- •Определить коэффициент регрессии b:
- •Решение:
- •Задача на определение коэффициента корреляции
Определим доверительный интервал для коэффициента корелляции

Определим параметры для расчета корреляционно-регрессионного уравнения

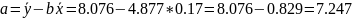
Рассчитаем теоретическое значение
Вывод
Табличное значение критерия Стьюдента равно 2,1448. Расчетное значение составляет 3.41. Исходя из этого, можно сделать вывод, что выборка, представленная в условии, удовлетворяет условия поставленной задачи.
Коэффициент корреляции r = 0,688. Исходя из этого можно сделать вывод, что данное корреляционно-регрессионное уравнение корректно.
Задание 2
Для заданной в условии выборки вычислить регрессию и найти доверительные интервалы коэффициентов регрессии и дисперсии для заданной доверительной вероятности. Вычислить полосу и коридор регрессии. Изобразить выборку графически на одном графике с линией регрессии. Изобразить графически полосу и коридор регрессии.
x |
-0.9 |
-0.8 |
-0.7 |
-0.6 |
-0.5 |
-0.4 |
-0.3 |
-0.2 |
y |
-2.169 |
-1,376 |
-0,974 |
-0,312 |
-0,314 |
-0,715 |
-0,312 |
1,119 |
x |
-0.1 |
0 |
0.1 |
0.2 |
0.3 |
0.4 |
0.5 |
|
y |
0.92 |
0.999 |
1.046 |
1.295 |
1.411 |
1.884 |
2.835 |
|
Представим исходные данные, а также линию регрессии на графике (рис.1). Каждая точка графика соответствует конкретной единице выборки; координаты точек определяются значениями переменных xi и yi. На основании поля корреляции можно выдвинуть гипотезу о том, что связь между всеми возможными значениями x и y носит линейный характер.
В результате анализа представленной графической информации установлено, что приведенный массив статистической информации можно описать с помощью корреляционно-регрессионного уравнения:

Алгоритм решения задачи
Определить коэффициент регрессии b:
Формулы для вычисления регрессии.
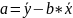 Определим
доверительный интервал коэффициента
регрессии:
Определим
доверительный интервал коэффициента
регрессии:

Формулы для вычисления доверительного интервала коэффициента регрессии:
Определим доверительный интервал коэффициента дисперсии:

Формулы для вычисления доверительного интервала коэффициента дисперсии.
Вычислим полосу регрессии:
Вычислим коридор регрессии:

Формулы для вычисления коридора регрессии:
№ |
x |
y |
xy |
x2 |
|
y-
|
1 |
-0,9 |
-2,169 |
1,952 |
0,81 |
-1,667 |
-0,502 |
2 |
-0,8 |
-1,376 |
1,101 |
0,64 |
-1,378 |
0,002 |
3 |
-0,7 |
-0,974 |
0,682 |
0,49 |
-1,089 |
0,115 |
4 |
-0,6 |
-0,312 |
0,187 |
0,36 |
-0,8 |
0,488 |
5 |
-0,5 |
-0,314 |
0,157 |
0,25 |
-0,511 |
0,197 |
6 |
-0,4 |
-0,715 |
0,286 |
0,16 |
-0,222 |
-0,493 |
7 |
-0,3 |
-0,312 |
0,094 |
0,09 |
0,067 |
-0,379 |
8 |
-0,2 |
1,119 |
-0,224 |
0,04 |
0,356 |
0,763 |
9 |
-0,1 |
0,92 |
-0,092 |
0,01 |
0,645 |
0,275 |
10 |
0 |
0,999 |
0 |
0 |
0,934 |
0,065 |
11 |
0,1 |
1,046 |
0,105 |
0,01 |
1,223 |
-0,177 |
12 |
0,2 |
1,295 |
0,259 |
0,04 |
1,512 |
-0,217 |
13 |
0,3 |
1,411 |
0,423 |
0,09 |
1,801 |
-0,39 |
14 |
0,4 |
1,884 |
0,754 |
0,16 |
2,09 |
-0,206 |
15 |
0,5 |
2,835 |
1,418 |
0,25 |
2,379 |
0,456 |
∑ |
-3 |
5,337 |
7,1007 |
3,4 |
|
|
|
|
yлев |
yправ |
(y- )2 |
|
( )2 |
-2,525 |
6,376 |
-1,761 |
-1,573 |
0,252 |
-0,7 |
0,49 |
-1,732 |
2,999 |
-1,472 |
-1,284 |
0.0004 |
-0,6 |
0,36 |
-1,33 |
1,769 |
-1,183 |
-0,995 |
0,013 |
-0,5 |
0,25 |
-0,668 |
0,446 |
-0,894 |
-0,706 |
0,238 |
-0,4 |
0,16 |
-0,67 |
0,449 |
-0,605 |
-0,417 |
0,039 |
-0,3 |
0,09 |
-1,071 |
1,147 |
-0,316 |
-0,128 |
0,243 |
-0,2 |
0,04 |
-0,668 |
0,446 |
-0,027 |
0,161 |
0,144 |
-0,1 |
0,01 |
0,763 |
0,582 |
0,262 |
0,45 |
0,582 |
0 |
0 |
0,564 |
0,318 |
0,551 |
0,739 |
0,076 |
0,1 |
0,01 |
0,643 |
0,413 |
0,84 |
1,028 |
0,004 |
0,2 |
0,04 |
0,69 |
0,476 |
1,129 |
1,317 |
0,031 |
0,3 |
0,09 |
0,939 |
0,882 |
1,418 |
1,606 |
0,047 |
0,4 |
0,16 |
1,055 |
1,113 |
1,707 |
1,895 |
0,152 |
0,5 |
0,25 |
1,528 |
2,335 |
1,996 |
2,184 |
0,042 |
0,6 |
0,36 |
2,479 |
6,145 |
2,285 |
2,473 |
0,208 |
0,7 |
0,49 |
|
25,898 |
|
|
2,072 |
|
2,8 |