
- •Раздел I. Статика (модули №1 и №2)
- •1. Системы сходящихся сил
- •1.1 Плоские системы сходящихся сил
- •1.2 Пространственные системы сходящихся сил.
- •2. Равновесие плоских систем произвольно расположенных сил
- •2.2 Контрольная работа с-3
- •Решение
- •3. Равновесие пространственных систем произвольно расположенных сил.
- •Методика решения задачи:
- •3.2 Контрольная работа с-6.
- •Методика выполнения задания:
- •Решение
- •Решение:
- •4. Центр тяжести тела
- •4.1 Контрольная работа с-8. Определение положения центра тяжести тела.
- •Площади и координаты центров тяжести некоторых плоских фигур
- •Методика решения контрольной работы
- •Решение
- •Раздел II.
- •5. Кинематика материальной точки (модуль №3)
- •5.1 Примеры решения типовых задач раздела кинематика точки
- •Решение:
- •Решение
- •Решение:
- •5.2 Примеры решения типовых задач раздела кинематика точки тела вращающегося вокруг неподвижной оси. Приложение №13 к Методическому пособию II семестр:
- •Решение:
- •Приложение №14 к Методическому пособию II семестр:
3. Равновесие пространственных систем произвольно расположенных сил.
3.1 Контрольная работа. С-7. Определение реакций опор пространственной ферменной конструкции, нагруженной произвольной пространственной системой сил. (смотри приложение №7 к настоящему «Методическому пособию…»).
Дано:
![]() Н,
Н,
![]() Н,
Н,
![]() см,
см,
![]() см,
см,
![]() см.
см.
Найти: реакции опор плиты NQCK (усилия в раскосах и стойках №№ 1 - 6). Схема ферменной конструкции показана на рисунке.
Методика решения задачи:
При решении задач, связаных с определением пространственной системы реакций опор ферменной конструкции, нагруженной произвольной пространственной системой сил, применим шесть уравнений равновесия:
Три уравнения равновесия сил в проекциях
на оси декартовых координат: 1)![]() ,
2)
,
2)![]() ,
3)
,
3)![]() ,
и
,
и
Три уравнения равновесия моментов в проекциях моментов сил вокруг осей декартовых координат:
4)![]() ,
5)
,
5)![]() ,
6)
,
6)![]() .
.
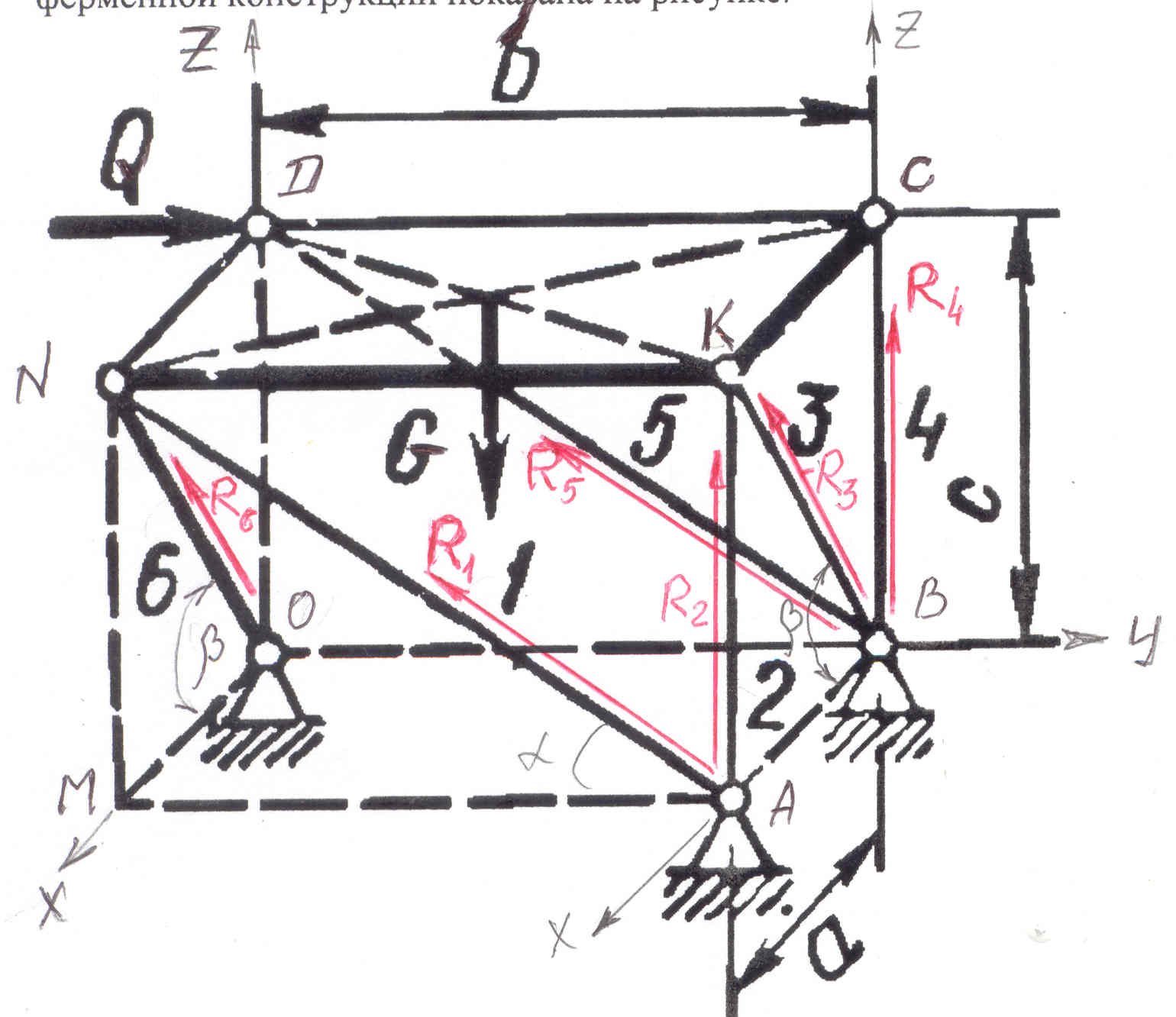
Указанная на картинке горизонтальная плита NDCK имеет вес G и к ней приложена в точке D горизонтальная сила Q. Плита опирается на шесть опор - стержней: наклонные раскосы 1, 3, 5, 6 и вертикальные стойки 2, 4.
Условимся считать все стойки сжатыми.
В этом случае реакции в стойках и раскосах
направлены в сторону плиты – т.е. вверх.
На рисунке направления реакций опор
показаны красными
векторами
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Для пространственной системы сил можно составить 6 уравнений равновесия, не расчленяя эту пространственную систему. В принципе, выбор координат декартовой системы, при этом, не имеет существенного значения, так как при 6 неизвестных мы имеем возможность составить для пространственной системы 6 уравнений равновесия. Поэтому выберем за начало декартовой системы точку О.
Для нахождения шести усилий
![]() в раскосах и стойках пространственной
системы сил составим 6 уравнений
равновесия:
в раскосах и стойках пространственной
системы сил составим 6 уравнений
равновесия:
- три уравнения проекций заданных сил и реакций опор на оси декартовых координат
1.
![]()
2.
![]()
3.
![]() и
и
- три уравнения моментов заданных сил и реакций опор вокруг осей декартовых координат
4.

5.

6.
![]()
Определим предварительно косинусы и синусы углов наклона раскосов 1, 3, 5, 6:
![]() ,
,
![]() ,
,
![]() ,
,
![]()
Из (1) определяем
![]() (7)
(7)
Из (2) определяем
![]() (8)
(8)
Из (5) определяем
![]() (9)
(9)
Подставим (9) в (3):
![]()
или
![]() (10)
(10)
Подставим (9) в (4):

или
![]() (11)
(11)
Подставим (7) в (10):
![]()
или ![]() или
или
![]() (12)
(12)
умножим (12) на b и подставим в (11):

или с учётом (7) находим
![]() и
и
![]() :
:
 ,
(13)
,
(13)
из (6) находим
![]() :
:
 ,
(14)
,
(14)
из (5) находим
![]() :
:
 ,
(15)
,
(15)
из (8) или из (2) находим
![]() :
:
![]() (16)
(16)
из (12) находим
![]() :
:
![]() ,
(17)
,
(17)
Подставив найденные значения реакций опор в уравнение (3), окончательно проверяем правильность вычислений ( в уравнении 3 присутствуют все 6 реакций опор):

Как видно из указанных вычислений, процедура определения реакций опор довольно громоздка и требует некоторой изобретательности.
Проверим возможность упрощения вычислений за счёт изменения расположения декартовой системы координат. Поместим начало координат в точку В. Составим 6 уравнений равновесия пространственной системы сил:
1.
2.
3.
4.

5.
6.
![]()
Из (4) находим
:

Из (1) находим
:

Из (6) находим
:

Из (5) находим
:

Из (2) находим
:
![]()
Из (3) находим :

упростим это равенство:

Все реакции опор совпадают с первым вариантом расположения декартовых координат. Тоесть:
|
|
|
|
|
|
|
|
|
|
|
|
Мы существенно упростили процесс определения реакций опор изменив положение начала декартовых координат.
Так как получили реакции опор , и со знаком минус, значит эти опоры оказались растянутыми.
