
- •Раздел I. Статика (модули №1 и №2)
- •1. Системы сходящихся сил
- •1.1 Плоские системы сходящихся сил
- •1.2 Пространственные системы сходящихся сил.
- •2. Равновесие плоских систем произвольно расположенных сил
- •2.2 Контрольная работа с-3
- •Решение
- •3. Равновесие пространственных систем произвольно расположенных сил.
- •Методика решения задачи:
- •3.2 Контрольная работа с-6.
- •Методика выполнения задания:
- •Решение
- •Решение:
- •4. Центр тяжести тела
- •4.1 Контрольная работа с-8. Определение положения центра тяжести тела.
- •Площади и координаты центров тяжести некоторых плоских фигур
- •Методика решения контрольной работы
- •Решение
- •Раздел II.
- •5. Кинематика материальной точки (модуль №3)
- •5.1 Примеры решения типовых задач раздела кинематика точки
- •Решение:
- •Решение
- •Решение:
- •5.2 Примеры решения типовых задач раздела кинематика точки тела вращающегося вокруг неподвижной оси. Приложение №13 к Методическому пособию II семестр:
- •Решение:
- •Приложение №14 к Методическому пособию II семестр:
Министерство образования и науки Украины
Национальный университет кораблестроения
имени адмирала Макарова
Феодосийский политехнический институт
Теоретическая механика
Методическое пособие
по выполнению самостоятельных расчётно-графических задач
и контрольных работ - II семестр
Разделы:
СТАТИКА,
КИНЕМАТИКА ТОЧКИ,
КИНЕМАТИКА ТВЕРДОГО ТЕЛА - поступательное и вращательное движение
Феодосия
Приморский
2010г
Предисловие:
Настоящее методическое пособие разработано в рамках программы кредитно-модульной системы организации учебного процесса по дисциплине «Теоретическая механика» для специальностей 8.100201, 8.090520, 8.090509, 8.090506 и является составной частью «Рабочей учебной программы …» по дисциплине «Теоретическая механика».
Методическое пособие охватывает учебную программу обучения студентов в объёме II семестра, соответствующую, как по содержанию, так и по объему, материалам содержательных модулей №1, 2, 3:
Модуль №1. (объем: Лекции – 25 баллов, Контрольные работы – 7 баллов, СРС – 6,5 баллов. Σ 38,5 баллов)
Модуль №2. (объем: Лекции – 10 баллов, Контрольные работы – 28 баллов, СРС – 4,3 баллов. Σ 42,3 баллов)
Модуль №3. (объем: Лекции – 10 баллов, Контрольные работы – 7 баллов, СРС – 2,2 баллов. Σ 19,2 баллов)
Раздел I. Статика (модули №1 и №2)
1. Системы сходящихся сил
Примеры решения расчетно-графических задач (РГЗ)
1.1 Плоские системы сходящихся сил
(Приложение №1 к настоящему Методическому пособию)
Целью этого тест-контроля является проверка усвоения темы «Плоская система сходящихся сил», а именно умение находить по параллелограмму сил реакции опор равнодействующую и уравновешивающую силы.
Пример №1-б.
Определить: направление и величину
реакций шарниров С и А, считая известным
направление и величину силы
![]() .
.
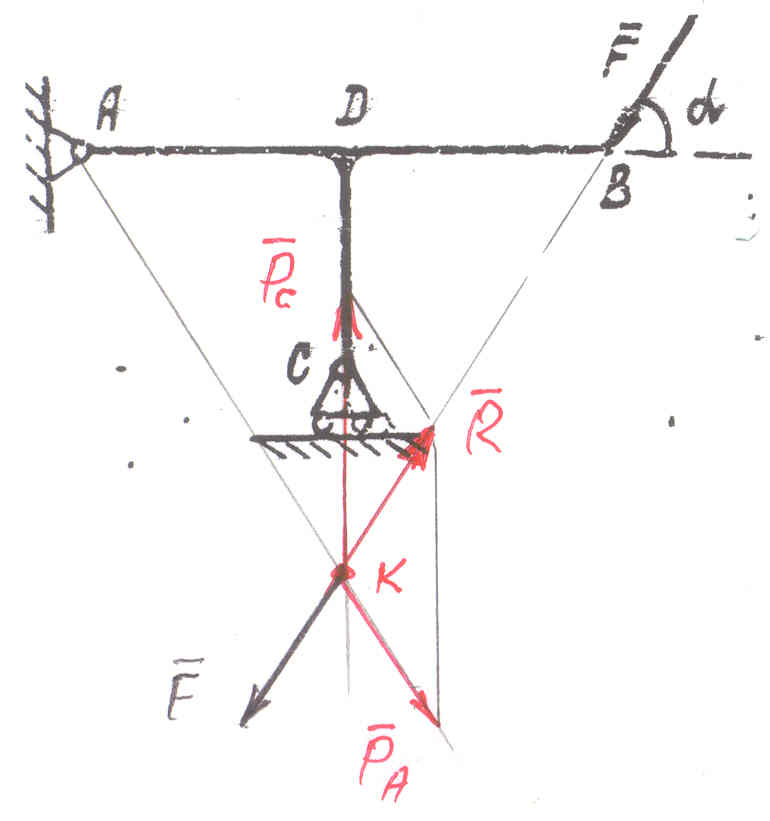 Решение:
Решение:
При решении задачи исходим из двух
свойств системы сходящихся сил: все
сходящиеся силы пересекаются в одной
точке (К) и находящаяся в равновесии
система сходящихся сил (реакции опор с
одной стороны и внешняя сила с другой
стороны) имеет равнодействующую реакций
опор силу
![]() ,
которая равна и противоположно направлена
внешней силе
,
выступающей как уравновешивающая по
отношению к этой равнодействующей и
следовательно к парралелограмму сил
образованным реакциями опор
,
которая равна и противоположно направлена
внешней силе
,
выступающей как уравновешивающая по
отношению к этой равнодействующей и
следовательно к парралелограмму сил
образованным реакциями опор
![]() ,
,
![]() .
Используя эти свойства плоской системы
сходящихся, находим точку пересечения
всех сил уравновешенной системы - точку
К. Для этого нам достаточно знать
направление любых двух сил системы. Нам
известно направление задаваемой внешней
силы
и
направление реакции катящейся опоры
С -
(она всегда перпендикулярна опорной
поверхности и направлена в противоположную
сторону от опорной поверхности – в
нашем случае – вертикально вверх).
Проведем до пересечения между собой
линии действия сил
и
.
Получим точку К. Эта точка и будет точкой
пересечения всех сил сходящейся системы
сил, в том числе и реакции связи шарнира
А, силы
.
Система сил
,
,
- это статическая система сходящихся
сил находящаяся в равновесии.
.
Используя эти свойства плоской системы
сходящихся, находим точку пересечения
всех сил уравновешенной системы - точку
К. Для этого нам достаточно знать
направление любых двух сил системы. Нам
известно направление задаваемой внешней
силы
и
направление реакции катящейся опоры
С -
(она всегда перпендикулярна опорной
поверхности и направлена в противоположную
сторону от опорной поверхности – в
нашем случае – вертикально вверх).
Проведем до пересечения между собой
линии действия сил
и
.
Получим точку К. Эта точка и будет точкой
пересечения всех сил сходящейся системы
сил, в том числе и реакции связи шарнира
А, силы
.
Система сил
,
,
- это статическая система сходящихся
сил находящаяся в равновесии.
Соединим шарнир А и точку К. Мы получили линию АК – направление действия силы . Отложим в точке К силу , равную по модулю силе и противоположно ей направленную. Это равнодействующая сила двух реакций связи - опор А и С. По правилу параллелограмма находим графически силы и .
Пример №2-б.
О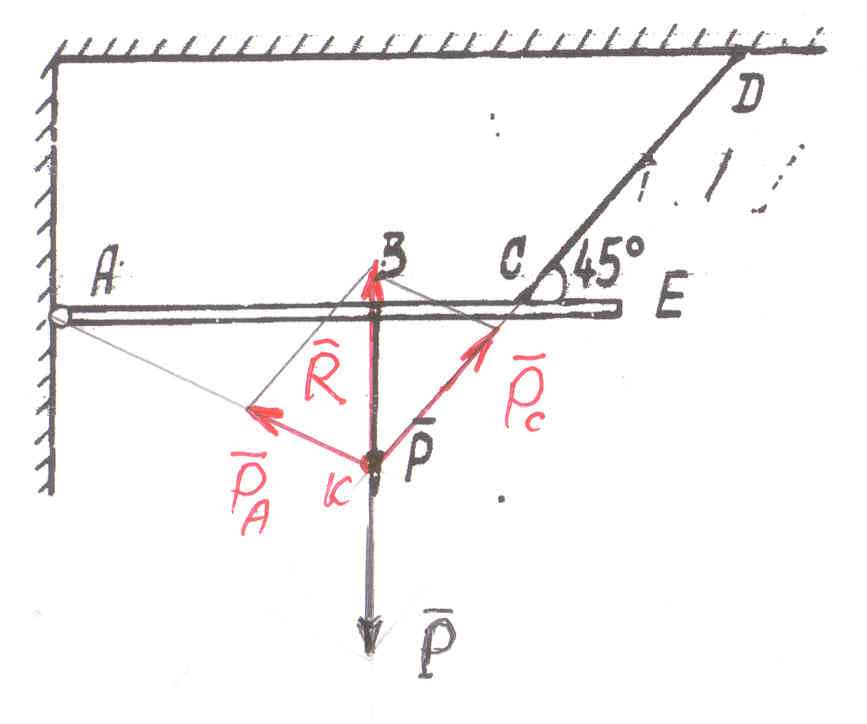 пределить:
направление и величину реакций связи
А и С, при известной заданной силе
пределить:
направление и величину реакций связи
А и С, при известной заданной силе
![]() .
.
Решение: Воспользуемся свойством
плоской системы сходящихся сил,
находящейся в равновесии. По известным
направлениям силы
и реакции связи в точке С
(нить СД однозначно определяет направление
действия своей реакции – только на
растяжение – в нашем случае – это вверх
под углом 450) и найдем точку
пересечения этих двух сил. Это будет
точка К. Построим по правилу параллелограмма
в этой точке равнодействующую силу
и обе реакции связей
и
![]() . Если строить систему сил в масштабе,
то можно получить не только направления
реакций связей но и модули их сил.
. Если строить систему сил в масштабе,
то можно получить не только направления
реакций связей но и модули их сил.
1.2 Пространственные системы сходящихся сил.
(приложение №5 к настоящему Методическому пособию)
Целью этого тест-контроля является проверка усвоения темы «Пространственная система сходящихся сил», а именно умение проецировать силы на оси и составлять уравнения равновесия пространственной системы сил.
Задача №1.
Определение усилий в стержнях АВ, АС,
АD, возникающих от действия
силы Р. Как в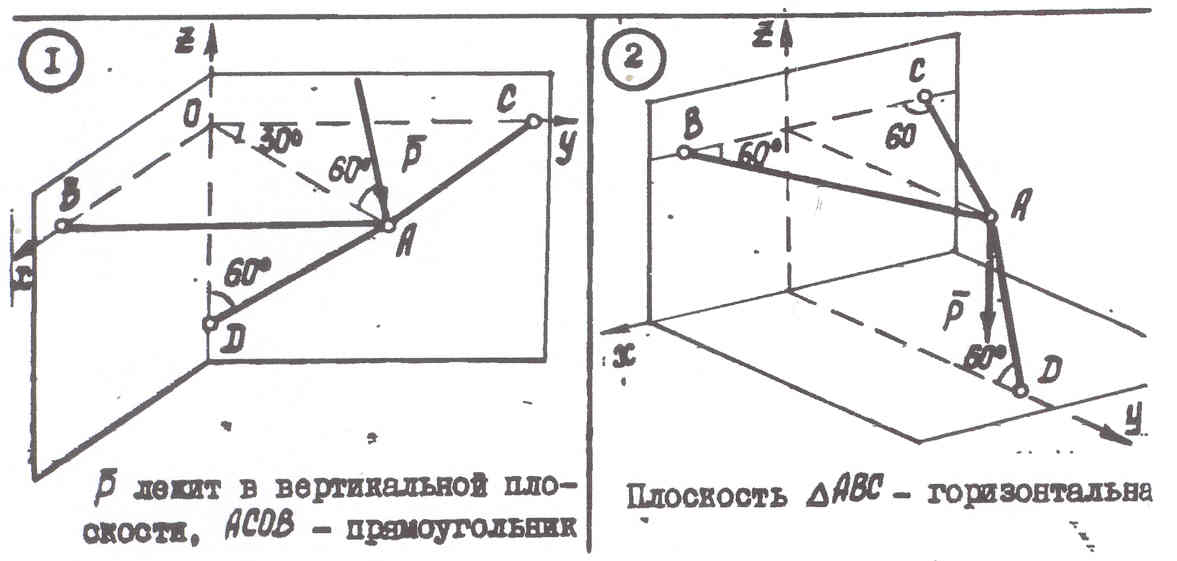 идно
из рисунка, сила Р расположена в
вертикальной плоскости ОАD
под углом 600 к горизонтальной
диагонали ОА прямоугольника АВОС.
Стержни АВ и АС расположены в горизонтальной
плоскости, стержень АD –
в вертикальной плоскости.
идно
из рисунка, сила Р расположена в
вертикальной плоскости ОАD
под углом 600 к горизонтальной
диагонали ОА прямоугольника АВОС.
Стержни АВ и АС расположены в горизонтальной
плоскости, стержень АD –
в вертикальной плоскости.
Пространственная система сходящихся
сил находится в равновесии тогда, когда
геометрическая сумма всех сил равна
нулю:
![]() .
Тогда и проекции этого равенства на оси
координат тоже равны нулю:
.
Тогда и проекции этого равенства на оси
координат тоже равны нулю:
![]()
![]()
![]()
Условимся считать стержни АВ и АС
растянутыми и, следовательно, реакции
опор
![]() и
и
![]() направленными от точки А, а стержень АС
сжатыми и, следовательно, реакцию опоры
направленными от точки А, а стержень АС
сжатыми и, следовательно, реакцию опоры
![]() направленной к точке А. Найдем суммы
проекций сходящейся системы сил на оси
координат:
направленной к точке А. Найдем суммы
проекций сходящейся системы сил на оси
координат:
![]() ,
т.к. проекция на ось X
реакции опоры В равна нулю.
,
т.к. проекция на ось X
реакции опоры В равна нулю.
![]() т.к. проекция на ось Y
реакции опоры C равна
нулю.
т.к. проекция на ось Y
реакции опоры C равна
нулю.
![]() т.к. проекции на ось Z
реакций опор C и В равны
нулю. Находим из этого равенства реакцию
опоры D:
т.к. проекции на ось Z
реакций опор C и В равны
нулю. Находим из этого равенства реакцию
опоры D:
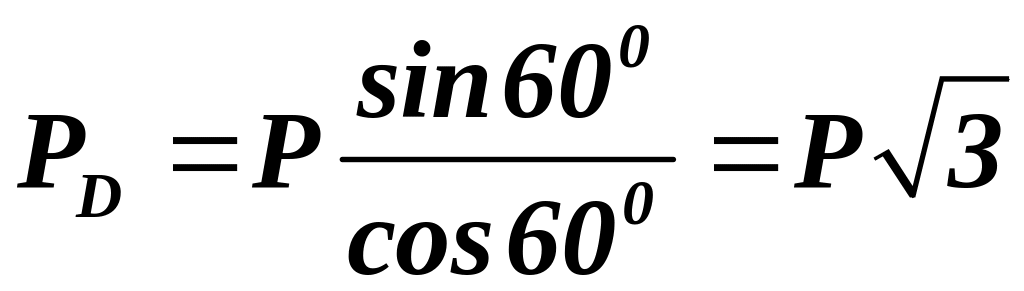 .
Тогда
.
Тогда
![]()
![]()
Итого:
![]() ,
,
![]() ,
,
![]() .
.
