ТВ / ИДЗ1

1. Непосредственный подсчет вероятностей в рамках классической схемы. Теоремы сложения и умножения вероятностей

Дано: Из полной колоды карт (52 листа) вынимаются сразу 4 карты.

Найти вероятность того, что все эти четыре карты будут разных мастей.

Решение:

Множество элементарных событий: вынимаем любую карту.

Множество благоприятных элементарных событий: вынимаем карту с «новой» мастью.

Условимся вынимать 4 раза по 1 карте. Тогда получим вероятность того, что все четыре карты будут разных мастей, равную произведению вероятностей:

В решении данной задачи использовалась формула умножения вероятностей.

Так как вынимаем 4 раза по 1 карте, то в первый раз мы можем вынуть любую из 52 карт, то есть вероятность благоприятного исхода равна 52/52=1. Во второй раз мы должны вынуть карту одной из 3 оставшихся мастей, то есть вероятность благоприятного исхода равна 39/51 (где 39 – количество карт нужных мастей, а 51 – оставшееся количество карт).

В третий и четвертый разы аналогичным образом получаем вероятности 26/50 и 13/49 соответственно. Так событие A заключается в совместном появлении всех 4 событий в описанном порядке, то получаем произведение вероятностей.

2. Формула полной вероятности и формула Байеса

Дано: Некто, выходя из точки А, на перекрёстках равновероятно выбирает любую дорогу кроме той, по которой пришёл.

Н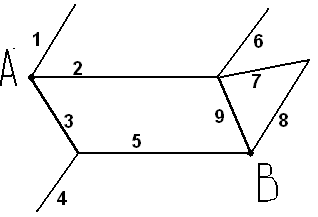 айти: Какова для него вероятность попасть в точку В?

Решение:

Основным событием A назовем событие, что некто дошел из A в B, в соответствии с условием задачи.

Гипотезами назовем выбор одной из 3 дорог по которым можно дойти из A в B или одной из 3 дорог в тупик. Всего 6 гипотез. Тогда по формуле полной вероятности получим:

,

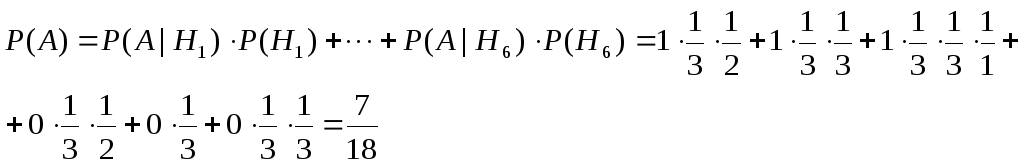где H1 соответствует пути A-3-5-B, H2 – пути A-2-9-B, H3 – пути A-2-7-8-B, H4 – пути A-3-4, H5 – пути A-1 и H6 – пути A-2-6

Так как все гипотезы образуют полную группу несовместных событий, то для решения задачи можем использовать формулу полной вероятности.

3. Повторение опытов (схема Бернулли).

Дано: На ВЦ от каждого из 10 отделов предприятия в течение рабочего дня с вероятностью 0,2 может поступить заявка на выполнение однотипных расчетов. Расчеты ведутся в ночное время, причем до начала рабочего дня может быть выполнено не более 5 заказов.

Найти вероятность того, что не все поступившие на ВЦ заказы будут выполнены.

Решение:

Пусть A – событие, соответствующее тому, что не все заказы выполнены, а B – событие, соответствующее тому, что все заказы выполнены.

Тогда для нахождения ответа, т.е. P(A) воспользуемся формулой P(A)=1-P(B).

Таким образом будем искать вероятность события обратного событию A, т.е. поступило заказов от 10 отделов.

Воспользуемся частной теоремой о повторении опытов. Так как поступление заказа из отделов – независимые события и вероятность их одинакова (p=0.2, q=1-p=0.8), то , где суммирование ведется по количеству поступивших заказов, а элементами суммы являются произведения вероятностей описывающих вероятность поступления заданного (j) числа заказов от отделов и непоступления заказов от остальных отделов (10-j). Таким образом получим P(A)=0.006.

Учитывая все вышесказанное использование теоремы о повторении опытов является обоснованным.