ТВ / ИДЗ2

Дано:

1. Вычисление вектора мат. ожиданий и ковариационных характеристик

случайного вектора:

• 1 способ

Для вычисления мат. ожиданий преобразуем выражение, стоящее под экспонентой, методом Лагранжа:

Значит вектор мат. ожиданий имеет вид: .

Для нахождения дисперсий и коэффициента корреляции сопоставим исходную плотность распределения с общей формулой.

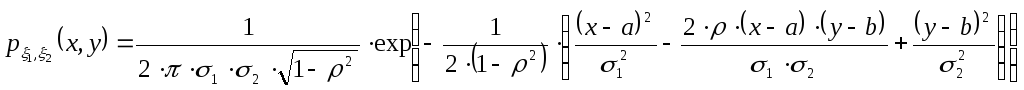
Откуда получим следующую систему:

• 2 способ

Найдем сначала неизвестную константу исходя из следующих соображений:

, т.е. и

Найдем теперь вектор мат. ожиданий.

Имеем

Следовательно плотности распределения имеют вид:

Откуда получен вектор мат. ожиданий .

Ковариационную матрицу мы можем найти также 2-мя способами:

• 1 способ

Ковариационная матрица – это матрица, обратная матрице квадратичной формы.

Матрица квадратичной формы: ;

Матрица ковариации: .

• 2 способ

Найдем 1 и 4 элемент матрицы ковариационной матрицы как дисперсии:

А 2 и 3 элементы равны и находятся по формуле .

Найдем .

Тогда второй и третий элементы будут равны: .

Имеем матрицу ковариации: , что совпало с вычисленной первым способом матрицей.

2. Найти ортогональное преобразование, переводящее соответствующий центрированный случайный вектор в вектор с независимыми компонентами.

Преобразование описывается следующим образом: , где A – ортогональная матрица, а B - вектор. Матрица A - матрица перехода от стандартного базиса к базису собственных векторов нашей матрицы квадратичной формы.

т.к. ковариационная матрица уже диагональная. Эта матрица ортогональна, следовательно, ортогонально и преобразование. Для центрирования данного случайного вектора надо отнять столбец математических ожиданий данных компонент, т.е. .

Тогда квадратичная форма станет:

Якобиан такой замены будет равен 1.

Следовательно, после такой замены, плотность случайного вектора принимает вид:

Данный вектор центрирован (математическое ожидание обоих компонент равно 0), имеет независимые друг от друга компоненты и получен ортогональным преобразованием.

Из такого вектора легко получить стандартный нормальный вектор. Достаточно сделать ещё одну замену.

На диагонали всегда будут находиться члены вида . Якобиан такой замены будет:

И умножив плотность распределения т. е. компонент предыдущей замены получим - плотность распределения стандартного и центрированного вектора.

3. Вычислить характеристики совместного распределения с.в. и записать его плотность.

За счет линейности мат. ожидания получим:

За счет независимости компонент можно рассчитать дисперсии следующим образом:

Теперь вычислим ковариации новых компонент вектора.

в силу независимости компонент.

Отсюда, матрица ковариации: .

Записываем плотность нового случайного вектора

, где .

Подставив все значения, получим:

.

Для проверки распределения составим матрицу квадратичной формы, ,

и найдем обратную к ней: - получили матрицу ковариации, что подтверждает верность наших расчетов.