3.3.2. Довірчий інтервал для генеральної середньої нормального розподілу при відомому

Нехай кількісна ознака генеральної сукупності розподілена за нормальним законом ( ), причому значення стандартного відхилення відоме.

Для оцінки генеральної середньої сформована вибірка об'єму й визначена вибіркова середня 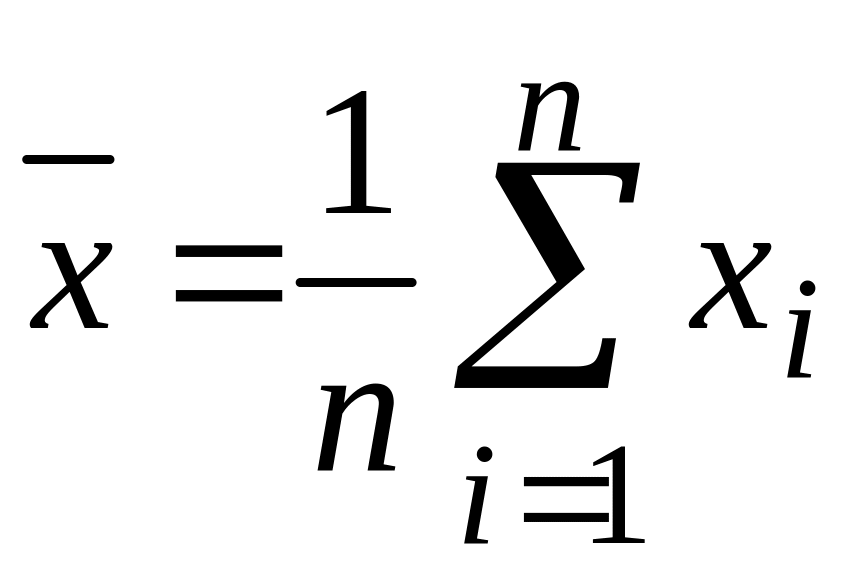. Потрібно оцінити невідоме значення генеральної середньої по вибірковій середній . Для цього знайдемо довірчий інтервал, що включає в себе генеральну середню з надійністю .

У силу випадковості вибірки будемо розглядати вибіркову середню як випадкову величину, розподілену за нормальним законом. Приймемо без доказу, що параметри нормального розподілу вибіркової середньої відповідно рівні: математичне очікування , середнє квадратичне відхилення 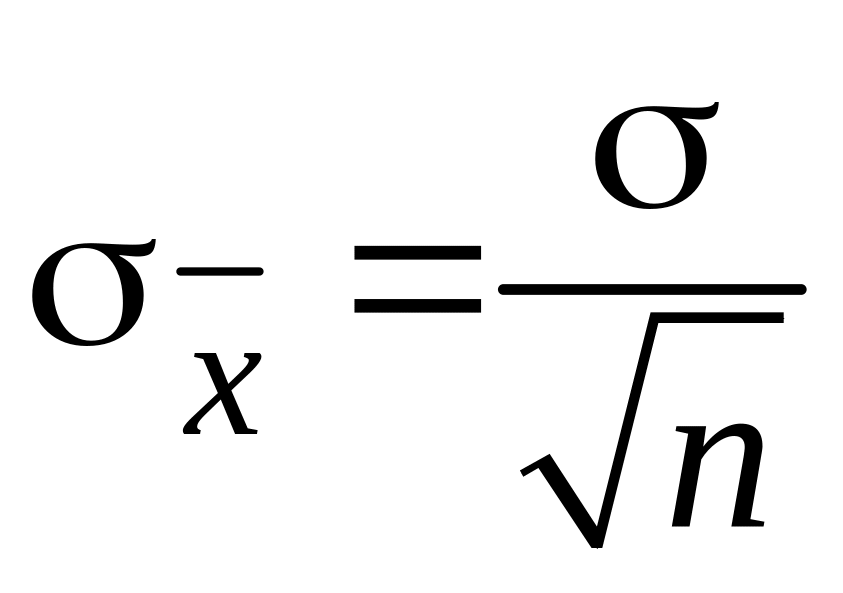, тобто .

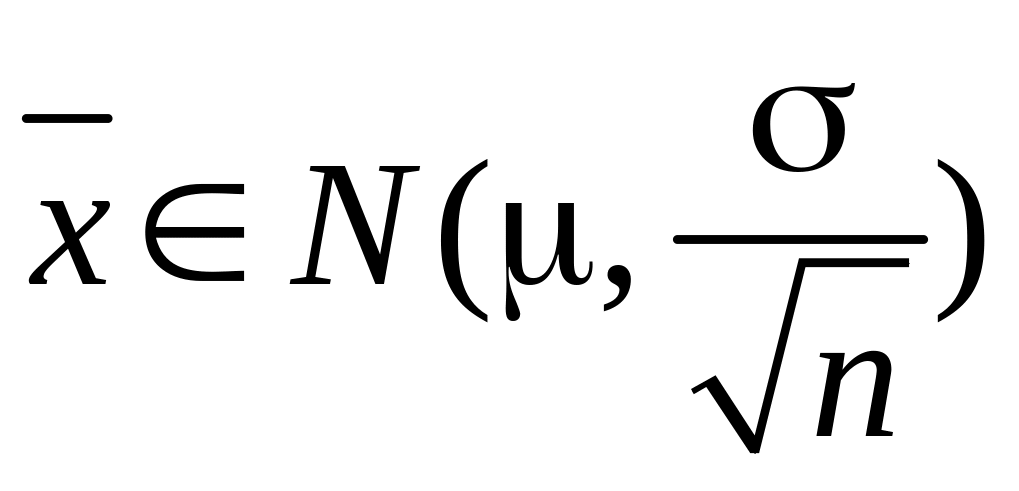Визначення. Величина називається стандартною помилкою вибірки.

По формулі (3.3) одержимо

. (3.5)

З іншого боку, для нормальної випадкової величини виконується умова

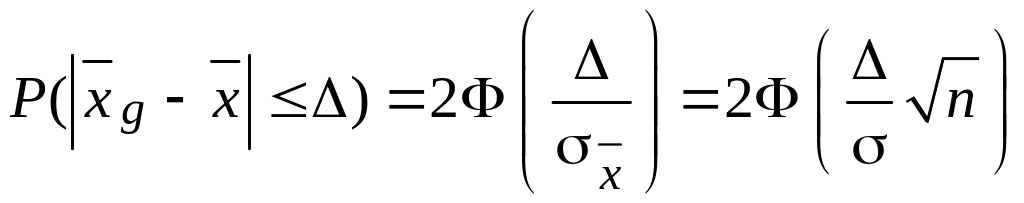. (3.6)

Позначимо

. (3.7)

Тоді, з урахуванням (3.5) і (3.6), запишемо

, (3.8)

. (3.9)

Тому що з (3.7) треба, що 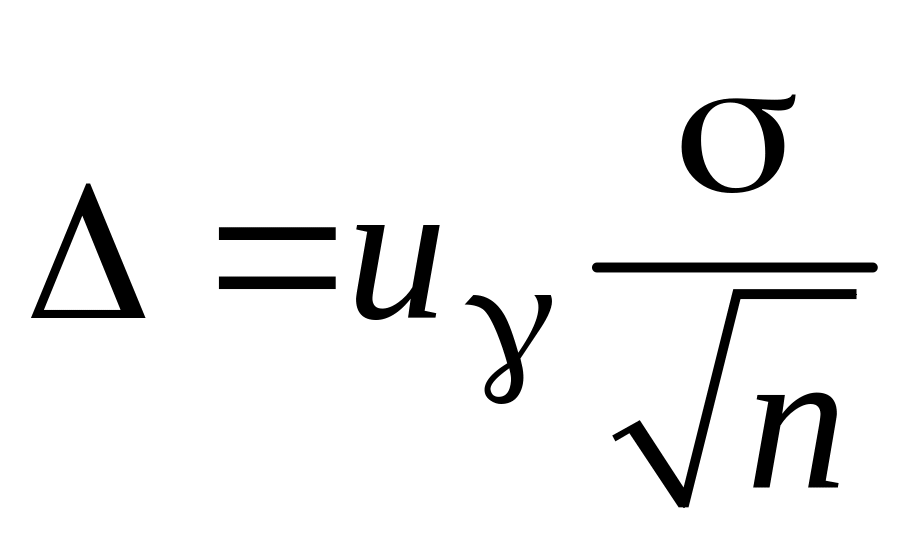, те (3.9) можна записати у вигляді

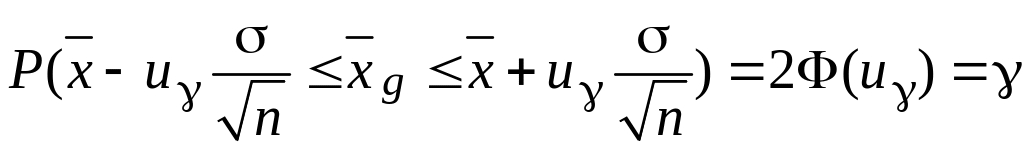. (3.10)

Вираз (3.10) визначає довірчий інтервал, що включає в себе генеральну середню з надійністю : якщо відома величина , то з імовірністю (надійністю) можна стверджувати, що значення знаходиться в інтервалі

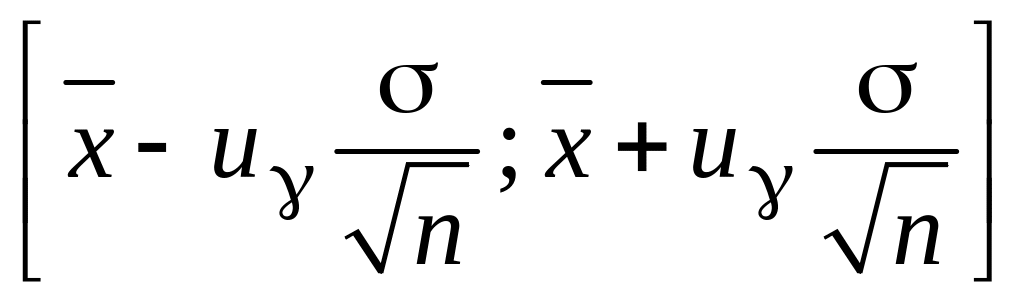. (3.11)

Величина залежить від довірчої ймовірності й визначається по таблиці функції Лапласа з умови

.

Наведемо деякі значення величини :

1) при : ;

2) при : ;

3) при : .

3.3.3. Довірчий інтервал для генеральної середньої нормального розподілу при невідомому

Нехай кількісна ознака генеральної сукупності розподілена за нормальним законом ( ), причому значення стандартного відхилення невідоме. Потрібно оцінити невідоме значення генеральної середньої по вибірковій середній .

Оскільки невідоме, то застосувати довірчий інтервал (3.11) для оцінки генеральної середньої неможливо. Однак за вибірковим даними можна побудувати випадкову величину

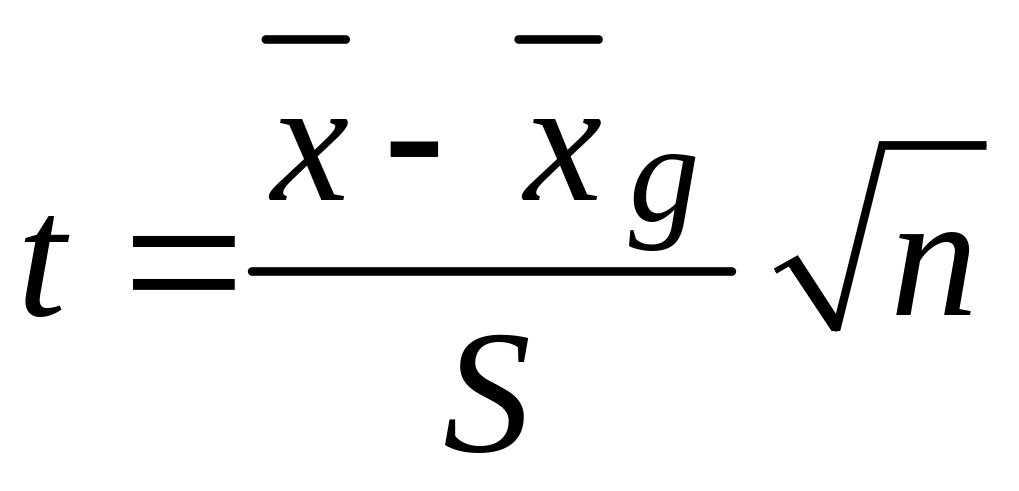, (3.12)

де S – незміщена оцінка стандартного відхилення генеральної сукупності, п – об'єм вибірки.

Відомо, що випадкова величина має розподіл Стьюдента² (t‑ розподіл) із числом ступенів свободи³ . Значення випадкової величини залежать як від довірчої ймовірності , так і від числа ступенів свободи, тобто .

Для побудови інтервальної оцінки генеральної середньої знайдемо по таблицях розподілу Стьюдента таку величину , для якої виконується умова

. (3.13)

Підставимо (3.12) в (3.13):

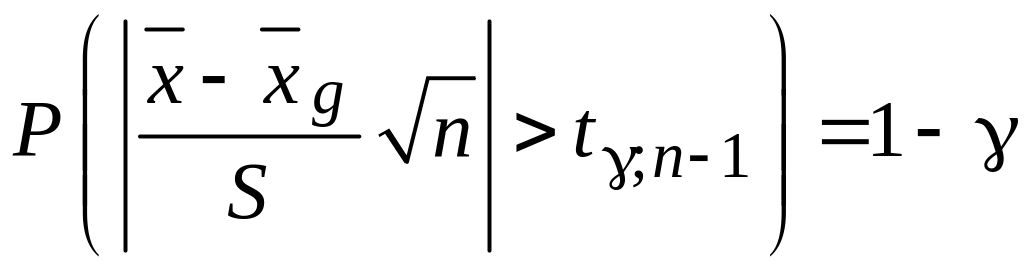. (3.14)

З огляду на те, що , перетворимо вираз (3.14):

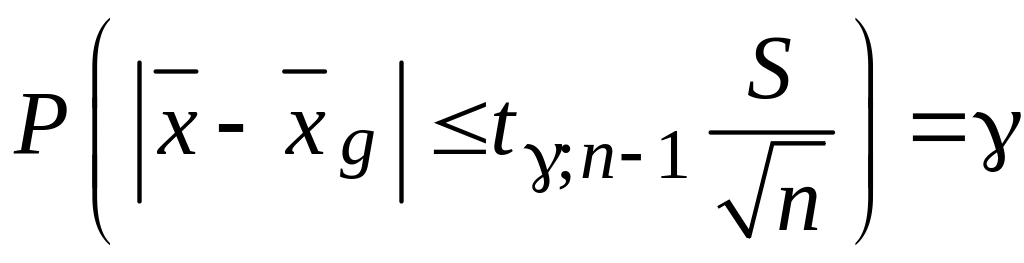, (3.15)

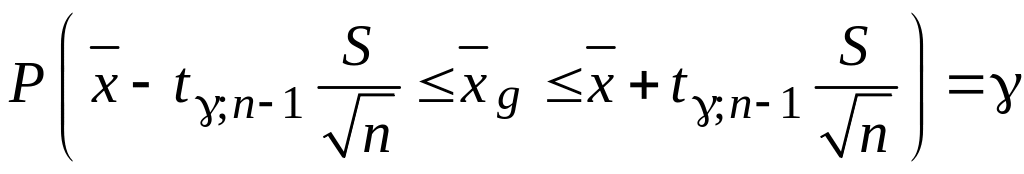. (3.16)

Вираження (3.16) визначає довірчий інтервал, що включає в себе генеральну середню з надійністю : якщо величина  невідома, то з імовірністю (надійністю) можна затверджувати, що значення перебуває в інтервалі

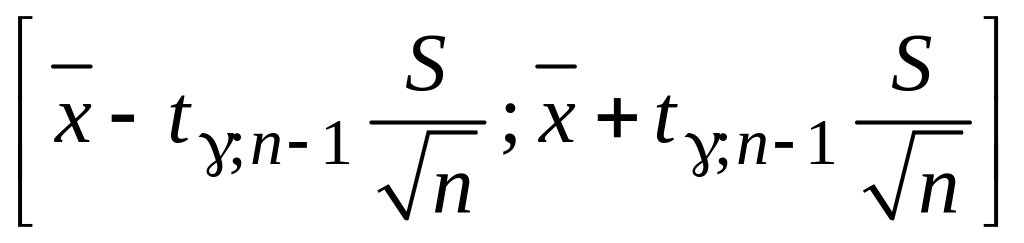. (3.17)

Формула (3.16) аналогічна формулі (3.10), однак між ними існує різниця, яка полягає в тому, що у формулі (3.16) коефіцієнт залежить не тільки від довірчої ймовірності , але й від об'єму вибірки n. Особливо це розходження помітно при малому числі спостережень. Так значенням n=10, =0,95 відповідають наступні значення коефіцієнтів і : і . Отже по формулі (3.10) буде отриманий менший довірчий інтервал, ніж по формулі (3.16). Це пояснюється тим, що при використанні розподілу Стьюдента враховується, що ніякої додаткової інформації про дисперсію генеральної сукупності , крім тієї, котру дає вибірка, немає. Тому використання нормального закону для оцінки параметра при малій кількості спостережень і невідомій дисперсії приводить до невиправданого звуження довірчого інтервалу. Якщо ж n, то розходження між довірчими інтервалами, що виражаються формулами (3.11) і (3.172), украй мале, тому що, як відомо, розподіл Стьюдента при необмеженому зростанні числа ступенів свободи наближається до нормального розподілу й .

Запишемо точність довірчого інтервалу при невідомому :

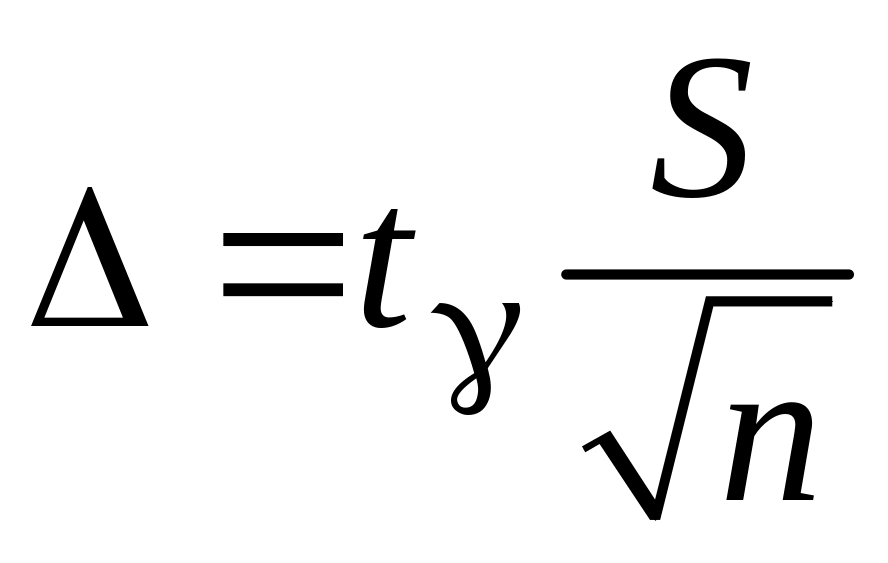. (3.18)