
- •1. Характеристики отраженной и преломленной волн при нормальном падении на границу двух диэлектриков
- •2. Формулы Френеля для частичных и общих энергетических коэффициентов отражения.
- •3. Основы электромагнитной теории дисперсии света.
- •4. Интерференция света
- •Сущность интерференции
- •Сложение колебаний. Когерентность и интерференция света
- •Интерференция волн (случай, когда колебания в слагаемых волнах происходят вдоль одной линии)
- •5. Методы получения когерентных пучков делением амплитуды.
- •Полосы равной толщины (Интерференция от пластины переменной толщины )
- •6. Многолучевая интерференция
- •Вычисление интенсивности лучей прошедших через пластину и отраженных от нее. Формулы Эйри
- •Зависимость интенсивности отраженных и проходящих пучков от разности фаз и коэффициента отражения
- •Определим ширину максимума из условия:
- •Многолучевые интерферометры. Интерферометр Фабри-Перо.
- •8. Дифракционная решётка.
- •Основные характеристики дифракционной решетки.
- •9. Подвійне променезаломлення. Еліптично-поляризоване світло.
- •Эллиптически поляризованный свет
- •Фотопружність. Ефекти Покельса, Керра , Фарадея.
8. Дифракционная решётка.
Дифракционной решёткой называется оптический элемент пропускание или отражение которого изменяется по периодическому закону. Наиболее простой дифракционной решёткой (далее ДР.) является набор щелей расположенных на одинаковом расстоянии друг от друга.
b-ширина щели; d=b+c-период ДР
Дифракционную картину от решётки можно найти двумя способами:
1.Решение интеграла, который описывает дифракцию Фраунгофера.
2.Сложением амплитуд поля, которые образуются в результате дифракции на
отдельных щелях. Тоесть дифракцыоная картина от решетки представляет
собой результат дифракции на каждой щели и интерференции волн от
различных щелей.
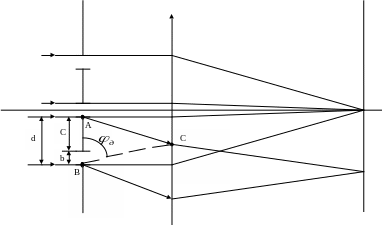
Амплитуда поля при дифракции от одной щели описывается (5.91):
V(φд)
=
V(0)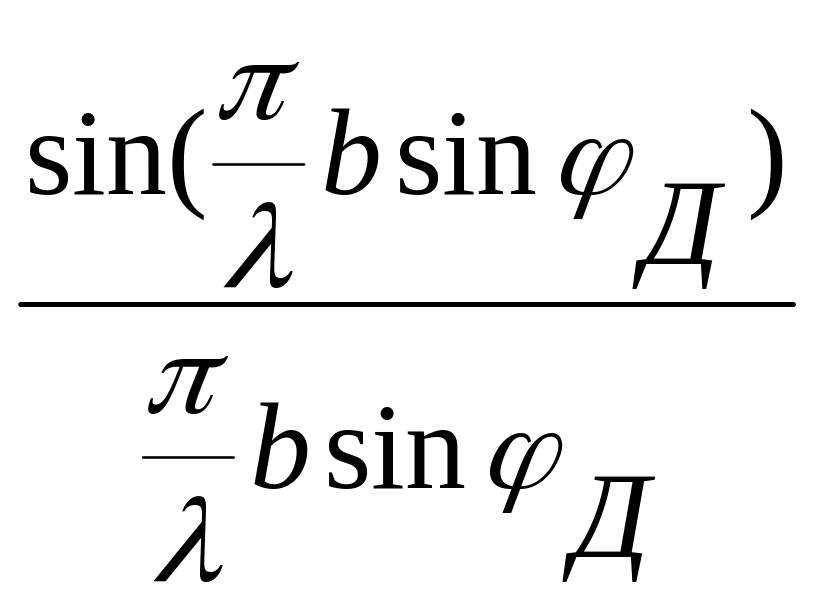 (5.95)
(5.95)
β
=
![]()
Определим разность хода и разность фаз между дифрагироваными волнами от соседних щелей.
∆ = АС = АВ∙sinд = d∙sinд (5.96)
δ
=
k∙∆
=
![]() (5.97)
(5.97)
Пусть дифрагированная световая волна (5.95) от нижней щели равна V1≡(5.95), тогда амплитуда от соседней щели:
V2=V1∙e-jδ
V3=V1∙e-j2δ
VN=V1∙e-j (N-1)δ
В результате интерференции этих волн образуется результирующие поле:
Vp = V1+V2+…+VN = V1(1+ e-jδ + e-j2δ +…+ e-j (N-1) δ)
Σ=![]() ,
где
a1=1
aN=e-j
(N-1) δ
q=e-jδ
,
где
a1=1
aN=e-j
(N-1) δ
q=e-jδ
Vp=V1 =V1
=V1 e-j
e-j
![]() (N-1)
(5.98)
(N-1)
(5.98)
Подставим (5.95) в (5.98):
VP(φд)
=V
(0)
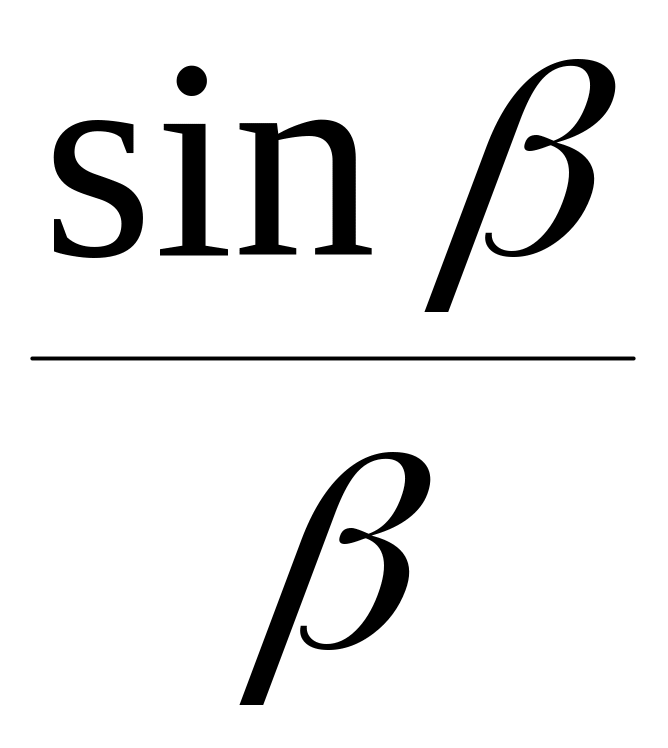 ∙
∙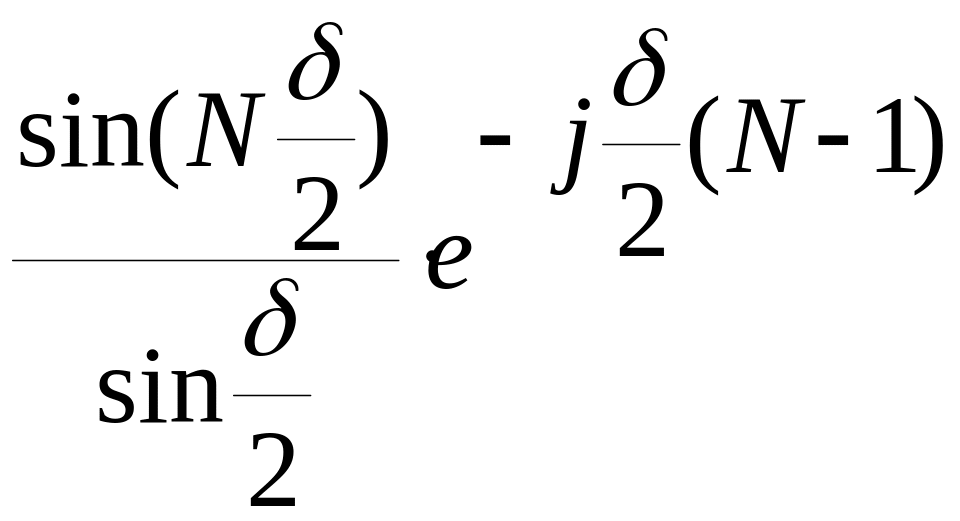 (5.99)
(5.99)
Интенсивность в дифракционной картине:
I(φд)=
│V(φд)
│2=[V(0)
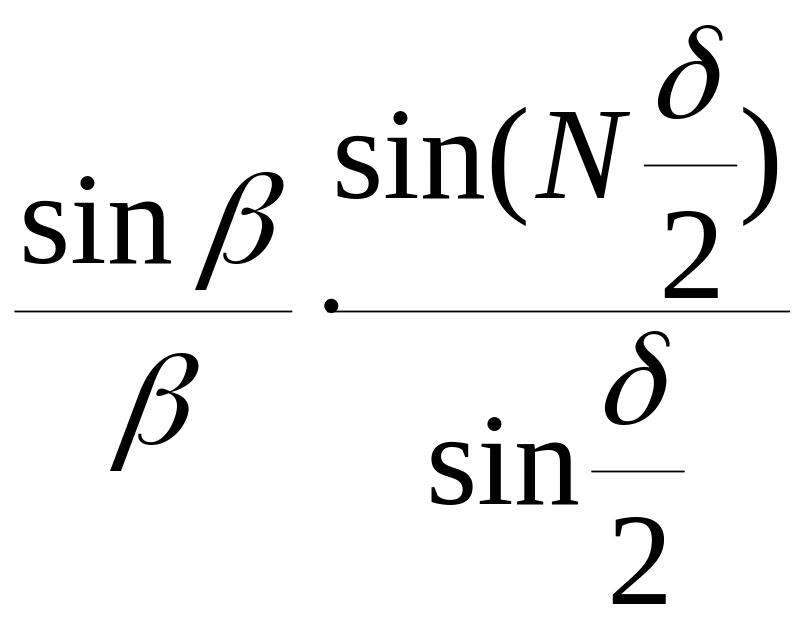 ]2
(5.100)
]2
(5.100)
Проанализируем распределение интенсивности (5.100) при дифракции на ДР.
Из (5.96) следует, что при выполнении условия:
d
sin![]() =
mλ
(5.101)
=
mλ
(5.101)
Разность хода между соседними щелями равна mλ что вызывает сложение всех световых волн от каждой щели по фазе или к существенному увеличению интенсивности. В результате этого образуются интенсивные максимумы, а условие (5.101) называется условием главных максимумов.
Между главными максимумами расположены минимумы которые находятся из условия:
I
(![]() )
= 0
)
= 0
Из (5.100):
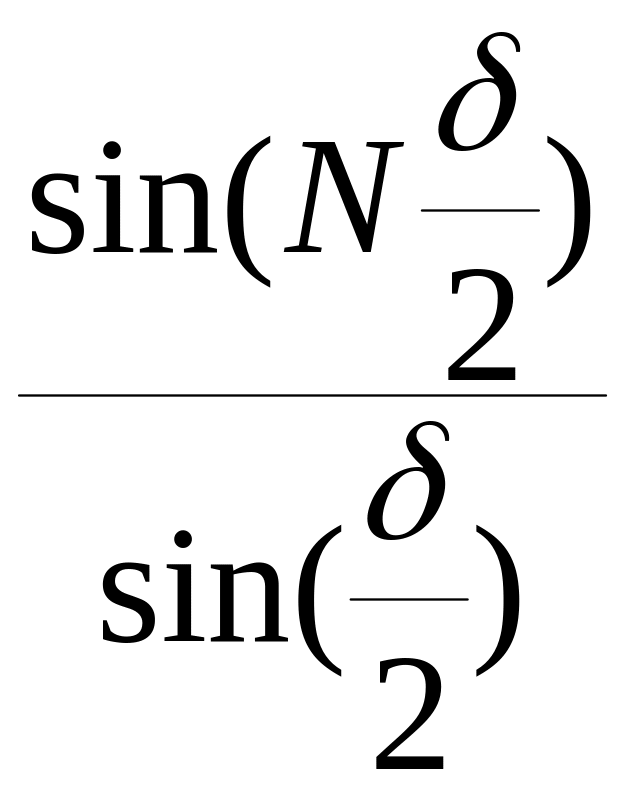 =
0
=
0
sin (N ) = 0
N = nπ
С
учетом (5.97):
![]() = nπ
= nπ
d
sin![]() =
=![]() λ
λ
если = m, то минимум (5.102) превращается в главный максимум (5.101) это означает, что между двумя главными максимумами расположено N-1 минимумов и
N-2 вторичных максимумов.
Определим интенсивность света в главном максимуме, для которого выполняется условие (5.101). Для этого подставим (5.101) в (5.100):
Im
=
│V
(0) │2
∙ (![]() )
2 [
)
2 [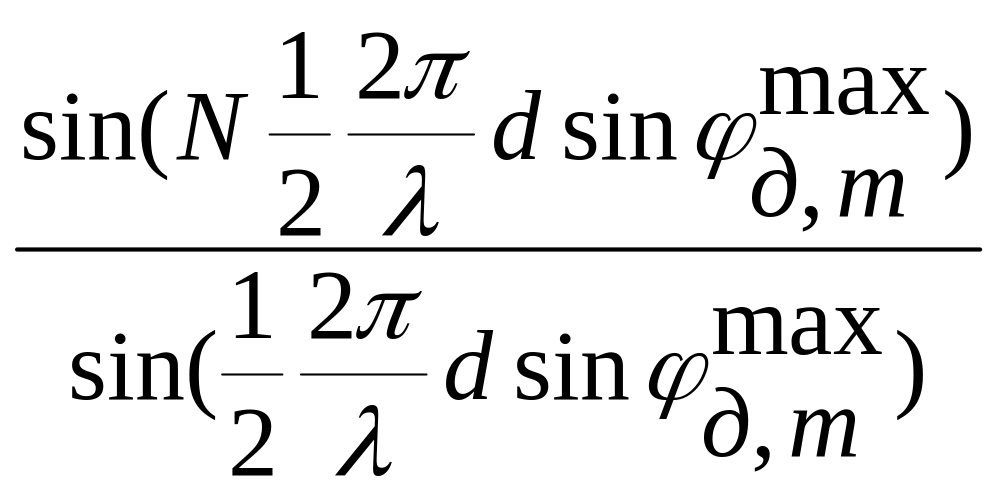 ]2
]2
[……]
=
 =
=
![]() = N
= N
β
=
![]()
Im
= │V
(0) │2( )2∙
N2
)2∙
N2
![]()
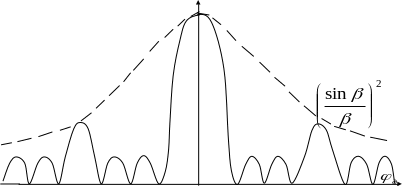
Из формул (5.100-5.103) следует, что:
1. Интенсивность главных максимумов пропорциональна квадрату числа щелей.
Im N2
Поэтому для получения больших интенсивностей этих максимумов используют
с большим N.
2. С увеличением порядка дифракции m интенсивность главных максимумов уменьшается.
Im
![]()
Поэтому дифракционные решетки используют при малых порядках m.
3.
 -
целое число, то главный максимум равен
нулю. Например, если в = с = ½ d
-
целое число, то главный максимум равен
нулю. Например, если в = с = ½ d
то все максимума равны нулю.
4. Из условия (5.101) следует, что положение m-ого максимума зависит от длины волны λ это означает, что дифракционная решетка способна разлагать белый свет на монохроматические составляющие.
