2.4 Касательная плоскость и нормаль
Пусть функция дифференцируема в точке , тогда для малых и можно записать
.
Положив
,
,
будем иметь:
.
Тогда:
.
В правой части приближенного равенства находится линейная функция относительно и , график которой является плоскостью. Таким образом, дифференцируемая функция в «небольшой» окрестности точки «похожа» на линейную функцию, а «небольшой» фрагмент ее графика «похож» на фрагмент плоскости, с которой график функции как бы «сливается».
Причем чем фрагмент меньше, тем он «более плоский».
В
качестве примера рассмотрим всюду
дифференцируемую функцию
.
Рассмотрим точку графика
.
Очевидно, что если мы будем уменьшать
фрагмент графика, содержащий точку
,
то он будет становиться все более и
более «плоским».
Рисунок 18
Плоскость, с которой «сливается» график дифференцируемой функции называется касательной плоскостью.
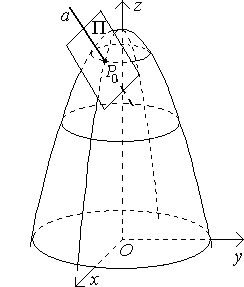
Рисунок 19
Пусть
дифференцируема в точке
,
то тогда через точку
ее графика проходит касательная плоскость
.
Вывод: если функция дифференцируема на некоторой области, то ее график представляет поверхность в виде одного сплошного куска (так как дифференцируемость влечет непрерывность) причем к этой поверхности всюду можно провести касательную плоскость, то есть график не имеет изломов, является как бы «гладким».
Прямую
(см. рисунок 19), проходящую через точку
,
и перпендикулярную касательной плоскости,
проходящей через эту точку, будем
называть нормалью.
Приведя уравнение касательной плоскости к общему уравнению плоскости, получим
.
Из
курса аналитической геометрии известно,
что плоскость, заданная уравнением
,
имеет нормальный вектор
.
Тогда
‑ нормальный вектор касательной
плоскости, который, очевидно, будет
являться направляющим вектором нормали.
Кроме
того, если прямая проходит через точку
и имеет направляющий вектор
,
то ее уравнение имеет вид
.
Теперь, зная, что нормаль имеет направляющий вектор и проходит через точку , получим уравнение нормали к графику функции , проходящей через точку графика
.
Перепишем уравнение касательной плоскости в виде
.
Тогда
в левой части записанного равенства
находится
‑ приращение аппликаты касательной
плоскости в точке
,
а в правой части имеем:
‑ дифференциал функции
в точке
.
Рисунок 20
Таким образом, мы получили геометрический смысл дифференциала функции двух переменных: дифференциал функции двух переменных равен приращению аппликаты касательной плоскости.
2.5 Дифференцируемость сложной функции
Теорема
2.5.1. Пусть функции
,
и
являются дифференцируемыми, тогда верна
формула для производной сложной функции
.
Доказательство.
Приращение
переменной
равное
вызовет приращения функций
и
,
которые мы обозначим
и
соответственно.
Так как функция дифференцируема, то существует представление
.
Разделим записанное равенство на
.
Перейдем
к пределу
.
Так
как функции
и
дифференцируемы, то они непрерывны, и
из того, что
следует
и
,
и тогда
и
.
Кроме того, из определения производной
функции одной переменной, имеем
,
и
.
Тогда получим равенство
,
.
Теорема доказана.
Пусть
теперь функции
и
зависят от двух переменных. Так как
частная производная по переменной
функции, зависящей от двух переменных
и
,
фактически сводится к производной
функции одной переменной
(переменная
принимается равной константе), то тогда
верна
Теорема 2.5.2.
Пусть функции , и являются дифференцируемыми.
Тогда верна формула для производной сложной функции
.
Замечание. Полученные формулы могут быть обобщены на случай функций переменных.
Выясним
теперь различия между полной
и частной
производными.
Пусть
имеется функция двух переменных
,
причем переменная
является функцией от
.
Используя формулу для производной сложной функции, получим
.
Рассмотрим функцию .
Рисунок 21
Величина влияет на непосредственно (сплошная стрелка) и через переменную (пунктирные стрелки). Так как при нахождении частной производной , переменная считается константой, то частная производная учитывает только непосредственное влияние на . В отличие от , полная производная учитывает и непосредственное влияние на , и влияние на через переменную . Именно поэтому производная называется полной производной.