1.4 Геометрическая интерпретация функций двух и трех переменных

Определение 1.4.1. Графиком функции двух переменных называется множество точек пространства

.

Как правило, графиком функции двух переменных является некоторая поверхность в пространстве.

Задача. Построить график функции методом сечений.

Решение.

1. Сечением графика плоскостью будет являться парабола

лежащая в плоскости .

2. Сечением графика плоскостью будет являться парабола

лежащая в плоскости .

3. При имеем равенство . Из которого следует, что и . Таким образом сечение графика плоскостью будет состоять из единственной точки – начала координат .

4. Сечение плоскостью будет являться окружность

На основании полученных данных строим график функции .

Рисунок 7

Полученная поверхность называется параболоидом вращения. В форме данной поверхности изготовляют спутниковые антенны и зеркала для телескопов.

Замечание 1. Очевидно, что с помощью графика двух переменных невозможно даже примерно определить значение функции при данных и . Чтобы иметь такую возможность применяются системы линий уровня.

Определение 1.4.2. Линией уровня функции двух переменных называется множество точек плоскости, удовлетворяющее уравнению .

Таким образом, на всей линии уровня значение функции остается постоянным. Очевидно, что линии уровня не могут пересекаться.

Если мы построим несколько линий уровня, меняя с некоторым шагом, то получим систему линий уровня – наглядное представление функции двух переменных.

Задача. Для функции построить семейство линий уровня.

Решение.

Так как функция определена на всей плоскости, то через каждую точку плоскости будет проходить линия уровня, причем единственная. Другими словами, линии уровня будут заполнять всю плоскость.

Получим уравнение линии уровня:

, , .

Полученное уравнение определяет кубическую параболу, а изменение величины приводит к параллельному переносу кубической параболы вдоль оси . Очевидно, что в данном случае может принимать любые действительные значения.

Взяв , например, с шагом 1, построим семейство линий уровня на координатной плоскости.

Рисунок 8

С помощью системы линий уровня легко можно находить примерные значения функции двух переменных.

В качестве примера рассмотрим характеристики некоторого биполярного транзистора. Для него зависимость тока коллектора от тока базы и напряжения коллектор-эмиттер приведена на рисунке 9.

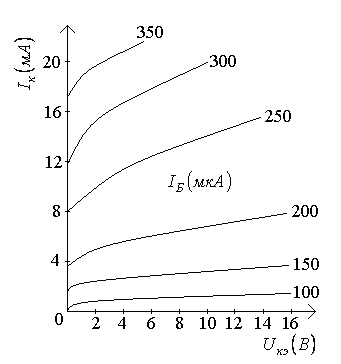
Рисунок 9

Из данной системы линий уровня мы можем легко определить примерное значение любого из параметров при условии, что нам известны значения двух других параметров.

Например:

1) если ток базы , а напряжение коллектор-эмиттер равно , то тогда ток коллектора ;

2) При ток коллектора будет, если ток базы .

Рассмотрим теперь функцию трех переменных . Для того, чтобы построить ее график нам нужна система координат с осями , , и . Таким образом, построить график функции трех переменных в трехмерном пространстве нельзя.

Для наглядного изображения функций трех переменных используются системы поверхностей уровня.

Определение 1.4.3. Поверхностью уровня функции трех переменных называется множество точек пространства, удовлетворяющее уравнению .

Таким образом, на всей поверхности уровня значение функции остается постоянным. Очевидно, что поверхности уровня не могут пересекаться.

Если мы построим несколько поверхностей уровня, меняя с некоторым шагом, то получим систему поверхностей уровня – наглядное представление функции трех переменных.

Задача. Для функции трех переменных построить семейство поверхностей уровня.

Решение.

Так как функция определена на всем пространстве, то через каждую точку будет проходить поверхность уровня, причем единственная. Другими словами, поверхности уровня будут заполнять все пространство.

Получим уравнение поверхности уровня:

, .

Отсюда следует, что . При записанное уравнение определяет точку .

Преобразуем полученное уравнение:

, .

Полученное уравнение при определяет эллипсоид с центром в начале координат и полуосями , и .

Взяв , построим семейство поверхностей уровня.

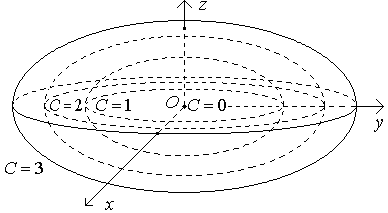
Рисунок 10