4.2 Глобальные экстремумы

Определение 4.2.1. Пусть функция определена на некоторой области . Будем говорить, что в точке функция имеет глобальный максимум (минимум), если для всех точек выполняется неравенство .

По второй теореме Вейерштрасса, непрерывная функция на ограниченном замкнутом множестве всегда достигает минимального и максимального значений, то есть имеет оба глобальных экстремума.

Очевидно, что глобальные экстремумы непрерывных функций могут достигаться либо на границе области , либо в точках локальных экстремумов, лежащих внутри области . Так как локальные экстремумы могут находиться только критических точках, то для нахождения глобальных экстремумов достаточно:

1) найти критические точки функции , лежащие внутри области ;

2) вычислить значения функции в этих точках;

3) найти минимальное и максимальное значения функции на границе области ;

4) выбрать из значений, найденных в пунктах 2) и 3), наименьшее и наибольшее.

Задача. Найти глобальные экстремумы функции в круге .

Решение.

1. Найдем критические точки функции , лежащие внутри круга .

, .

Полученные частные производные первого порядка существуют всюду на . Найдем стационарные точки, решив систему

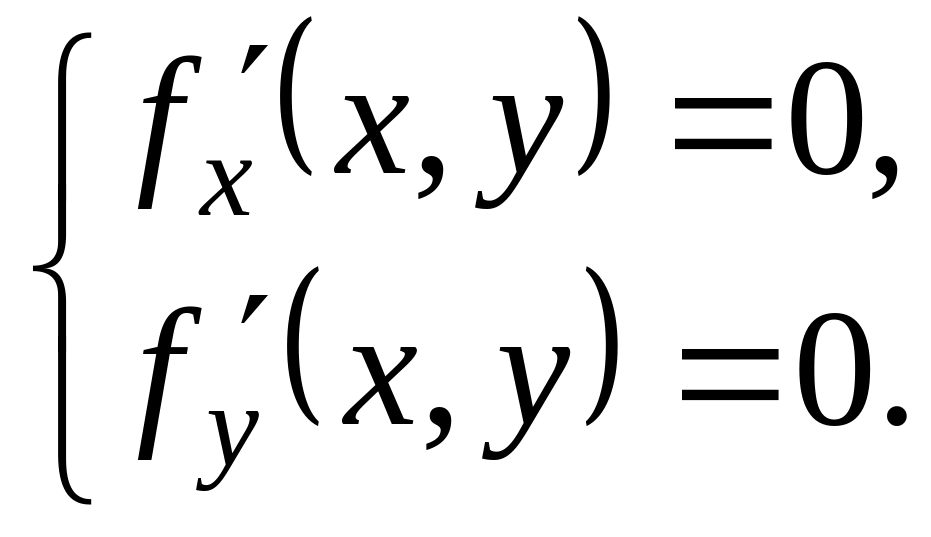
Очевидно, что ‑ единственная стационарная точка функции . Она принадлежит кругу .

2. Найдем значение функции в стационарной точке .

.

3. Найдем минимальное и максимальное значения функции на границе круга , то есть на окружности .

Зададим окружность в параметрической форме. Получим:

, где .

Подставив выражения для и в функцию , будем иметь функцию одной переменной .

Из свойств функции получаем, что минимальное значение функции на отрезке будет равно и оно будет достигаться при (точка ) и при (точка ), а максимальное значение будет равно и оно будет достигаться в точках (точка ), (точка ), (точка ).

4. Выбрав из значений, полученных в пунктах 2 и 3, минимальное и максимальное значения, получим глобальные экстремумы.

1) , минимальное значение функции достигается в точках , ;

2) , максимальное значение функции достигается в точках , .

Задача. Найти глобальные экстремумы функции в треугольнике ограниченном прямыми , и .

Решение.

1. Сделаем чертеж.

Рисунок 30

2. Найдем критические точки функции , лежащие внутри треугольника .

,

.

Полученные частные производные первого порядка существуют всюду на . Найдем стационарные точки, решив систему

Очевидно, что ‑ единственная стационарная точка функции . Она принадлежит треугольнику .

3. Найдем значение функции в стационарной точке .

.

4. Найдем минимальное и максимальное значения функции на границе треугольника .

Граница треугольника состоит из трех отрезков: , и .

Отрезок : , .

.

Отсюда следует, что минимальное значение функции при достигается при и равно .

Найдем еще значения функции на концах отрезка . Получим и .

Получили, что минимальное значение функции на отрезке равно , а максимальное значение равно .

Отрезок : , .

.

Отсюда следует, что минимальное значение функции при достигается при и равно .

Найдем еще значения функции на концах отрезка . Получим и .

Получили, что минимальное значение функции на отрезке равно , а максимальное значение равно .

Отрезок : , .

.

Минимум этой функции достигается в точке вершины параболы , и он равен .

Найдем еще значения функции на концах отрезка . Получим и .

Получили, что минимальное значение функции на отрезке равно , а максимальное значение равно .

Таким образом, на границе треугольника минимальное значение функции равно , а максимальное значение равно .

5. Из пунктов 3-4 имеем, что:

1) , минимальное значение функции достигается в точке ;

2) , максимальное значение функции достигается в точке .