3.3 Формула Тейлора
Теорема
3.3.1. Пусть для функции
в некоторой окрестности
точки
существует
-ый
дифференциал, тогда в
верна формула Тейлора с остаточным
членом в форме Лагранжа
.
Доказательство.
Пусть
точка
принадлежит окрестности
.
Зафиксируем
,
,
,
и рассмотрим функцию
.
Введенная
функция на отрезке
имеет производные до порядка
включительно. Тогда для нее можно
записать формулу Маклорена с остаточным
членом в форме Лагранжа
.
Положив
,
будем иметь
. (3)
Вернемся к функции .
1.
.
2.
.
3.
►Используем формулу для производной сложной функции
,
где , , .◄
.
Аналогично можно показать, что:
1)
;
2)
.
Подставив
в (3) выражения для
,
,
,
…,
,
,
получим формулу Тейлора с остаточным
членом в форме Лагранжа
.
Теорема доказана.
Если функция имеет в точке -ый дифференциал, то тогда в некоторой окрестности точки верна формула Тейлора с остаточным членом в форме Пеано
.
Здесь:
‑ точка с координатами
.
Примем данное утверждение без доказательства.
4 Экстремумы функций нескольких переменных
4.1 Понятие экстремума функции нескольких переменных. Необходимое условие экстремума. Достаточное условие экстремума
Определение
4.1.1. Будем говорить, что функция
имеет в точке
максимум (локальный максимум), если
можно указать такую проколотую окрестность
точки
,
для всех точек этой окрестности будет
выполняться неравенство
.
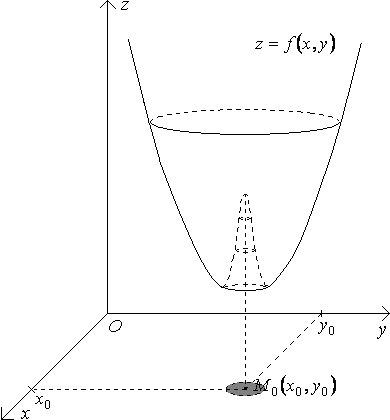
Рисунок 27
Определение
4.1.2. Будем говорить, что функция
имеет в точке
минимум (локальный минимум), если можно
указать такую проколотую окрестность
точки
,
для всех точек этой окрестности будет
выполняться неравенство
.
Рисунок 28
Точки, в которых функция имеет максимум или минимум, называются точками экстремумов.
Теорема
4.1.1. Пусть в точке
функция
имеет экстремум, и существуют частные
производные первого порядка
и
,
то тогда они равны 0.
Доказательство.
Пусть в точке функция имеет максимум (в случае минимума – доказательство аналогично).
По условию существует . По определению частной производной будем иметь
►Так
как в точке
имеется максимум, то для достаточно
малых
будем иметь
.
Тогда получим
.
Кроме того, из
следует
.
Отсюда
.
Далее используем, что предел отрицательной
величины является неположительным.◄
.
С другой стороны
►Так
как в точке
имеется максимум, то для достаточно
малых
будем иметь
.
Тогда получим
.
Кроме того, из
следует
.
Отсюда
.
Далее используем, что предел положительной
величины является неотрицательным.◄
.
Из
соотношений
и
следует равенство
.
Аналогично
можно доказать, что
.
Теорема доказана.
Замечание 1. Из данной теоремы следует, что функция может иметь экстремум, только в критических точках, то есть в точках, где все частные производные равны 0 (такие точки называются стационарными) или не существуют. Таким образом, доказанная теорема выражает необходимое условие экстремума.
Следует
отметить, что данное необходимое условие
не является достаточным. Действительно,
рассмотрим функцию
.
Для
нее имеем
,
.
Обе частные производные в точке
равны 0, но в начале координат данная
функция (см. рисунок 29, на котором показаны
знаки функции
в координатных углах) очевидно экстремума
не имеет.
Рисунок 29
Теперь
рассмотрим достаточное условие экстремума
функции двух переменных. С целью упрощения
преобразований введем следующие
обозначения:
,
,
,
.
Теорема 4.1.2. Пусть выполняются условия:
1) ‑ стационарная точка функции ;
2) функция дважды непрерывно дифференцируема в точке .
Тогда:
1)
если
,
то в точке
функция
не имеет экстремума;
2)
если
,
то в точке
экстремум может, как быть так и не быть;
3)
если
,
то в точке
функция
имеет экстремум (если
‑ минимум, а если
‑ максимум).
Доказательство.
Запишем
формулу Тейлора в окрестности точки
при
с остаточным членом в форме Пеано
.
Так
как
‑ стационарная точка функции
,
то
и
.
Отсюда следует, что
.
Таким образом, получаем:
.
Так
как при сужении окрестности точки
слагаемое
является бесконечно малой более высокого
порядка, чем бесконечно малая
,
то в достаточно узкой окрестности точки
знак разности
будет определяться знаком
.
Рассмотрим
►Так
как в определении экстремума фигурирует
проколотая окрестность точки
,
то разности
и
не могут одновременно обращаться в 0.
Рассмотрим случай, когда
.
Случай
рассматривается аналогично.◄
►Введем
обозначение
.◄
.
Если
,
то квадратный трехчлен
имеет отрицательный дискриминант, что
влечет сохранение знака квадратного
трехчлена при любом
.
Таким образом, знак разности
сохраняется в достаточно узкой проколотой
окрестности точки
.
Отсюда следует наличие экстремума в
этой точке.
В
случае
имеем
‑ в точке
имеется минимум, а если
,
то
‑ в точке
имеется максимум.
Пусть
теперь
.
Тогда квадратный трехчлен
имеет положительный дискриминант, что
влечет наличие у него действительных
корней. В этом случае трехчлен (и,
следовательно, разность
)
может принимать как положительные, так
и отрицательные значения. В этом случае
в точке
нет экстремума.
Теорема доказана.
Замечание
2. Если
,
то в стационарной точке
экстремум может, как быть, так и не быть.
Например,
функции
,
,
имеют стационарную точку
,
для которой
.
Первая функция в начале координат не
имеет экстремума, вторая имеет минимум,
а третья – максимум.
Замечание 3. Из замечания 2 следует, что доказанное достаточное условие экстремума не являются необходимым.
Задача.
Найти экстремумы функции
.
Решение.
1. Используем необходимое условие экстремума. Для этого найдем все частные производные первого порядка данной функции:
1)
;
2)
.
Полученные частные производные существуют при любых значениях и . Тогда найдем стационарные точки, решив систему уравнений
.
Данная система уравнений имеет множество решений
.
Получили
четыре стационарные точки:
,
,
,
.
2. Используем достаточное условие экстремума. Для этого найдем частные производные второго порядка:
1)
;
2)
;
3)
.
Исследуем найденные стационарные точки на экстремум.
Стационарная точка .
,
,
.
Так
как
,
то в точке
данная функция не имеет экстремума.
Стационарная точка .
,
,
.
Так
как
,
то в точке
данная функция не имеет экстремума.
Стационарная точка .
,
,
.
Так
как
,
то в точке
данная функция имеет экстремум. Из того,
что
следует, что в точке
имеется минимум
.
Стационарная точка .
,
,
.
Так
как
,
то в точке
данная функция имеет экстремум. Из того,
что
следует, что в точке
имеется максимум
.