2.9 Производная по направлению. Градиент

Нам уже известно, что частные производные и характеризуют скорость изменения функции при перемещении из точки вдоль осей и соответственно.

Для того чтобы охарактеризовать скорость изменения функции при перемещении из точки в произвольном направлении, используется понятие производной по направлению.

Определение2.9.1. Производной функции в точке с радиус-вектором в направлении единичного вектора называется число

.

Часто единичный вектор задают с помощью направляющих косинусов: или , где , и ‑ углы, которые образует вектор с положительными направлениями осей координат.

Выведем формулу для вычисления производной по направлению. Пусть функция дифференцируема в точке , тогда существует представление

.

Положив , , будем иметь

.

Разделим полученное равенство на . Получим:

или в других обозначениях

.

Перейдя в записанном равенстве к пределу при , получим формулу для нахождения производной по направлению

или в других обозначениях

.

Замечание. Частные производные и являются частными случаями производной по направлению при и соответственно.

Для функций нескольких переменных вводится еще и векторная величина, характеризующая изменение функции.

Определение 2.9.2. Градиентом функции называется вектор

.

С помощью понятия градиента формулу для вычисления производной по направлению можно записать в виде

.

Используя формулу для скалярного произведения , получим

,

где ‑ угол между векторами и .

Из последнего равенства следует, что производная по направлению будет максимальна когда . Таким образом, направление градиента совпадает с направлением наибыстрейшего возрастания функции , а модуль градиента характеризует максимальную скорость возрастания функции по величине:

.

Можно показать, что вектор градиента всегда перпендикулярен соответствующей линии уровня

Рисунок 23

Используем, что угловой коэффициент нормали, проведенной к графику функции в точке с абсциссой , равен [3, стр. 221].

Пусть в окрестности точки линия уровня является графиком функции , тогда используя формулу для производной неявной функции, получим угловой коэффициент нормали

.

Определим теперь угловой коэффициент прямой, содержащей вектор градиента .

Рисунок 24

Из треугольника имеем .

Получили, что угловые коэффициенты нормали к линии уровня и прямой, содержащей вектор градиента, совпадают. Таким образом, градиент перпендикулярен линии уровня.

Задача. Дана (рисунок 25) система линий уровня функции . Требуется определить знаки производных по направлению , и сравнить их модули. Определить направление вектора градиента .

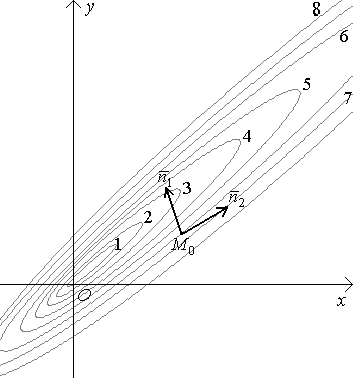
Рисунок 25

Решение.

1. Из приведенной системы линий уровня, очевидно, что в направлении вектора функция убывает, а в направлении вектора ‑ растет. Тогда имеем, что , а .

2. В направлении вектора скорость изменения функции явно больше, чем в направлении вектора . Отсюда следует, что .

3. Вектор градиента перпендикулярен линии уровня, проходящей через точку , и направлен в сторону возрастания значений функции .

Рисунок 26