Лабораторная работа 3 / 2008-05-12-23-15-Маша-3

Санкт-Петербургский государственный электротехнический университет «ЛЭТИ»

Кафедра АСОИУ

Отчет по лабораторной работе №3

Вариант 3

. ФКТИ, Группа 5362

Преподаватель:Матевицкая Н.Е.

Санкт-Петербург, 2007

z=20x₁+30x₂→min(max)

При ограничениях:

y₁=3x₁+3x₂≤15 (1)

y₂=2x₁+6x₂≤18 (2)

y₃=4x₁ 2 ≤y₄≤16

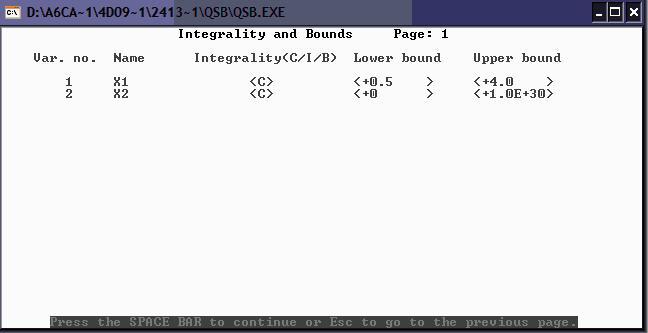
Для удобства 3 ограничение запишем в виде: 0,5 ≤x₁≤4 (3)

y₄=x₁+2x₂ 1 ≤y₄≤8 (4)

y₅=x₁-x₂≤1,5 (5)

Задача на минимизацию:

1) Ввод новой задачи:

Диалоговая настройка модели:

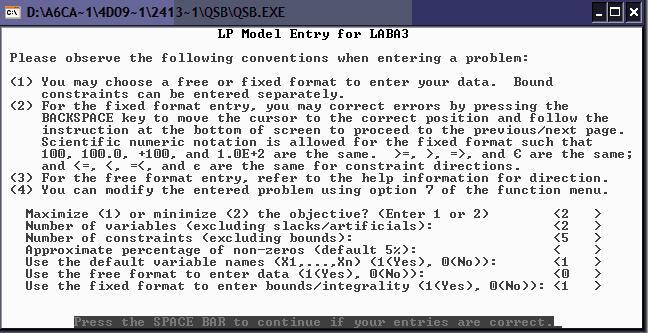
Ввод данных:

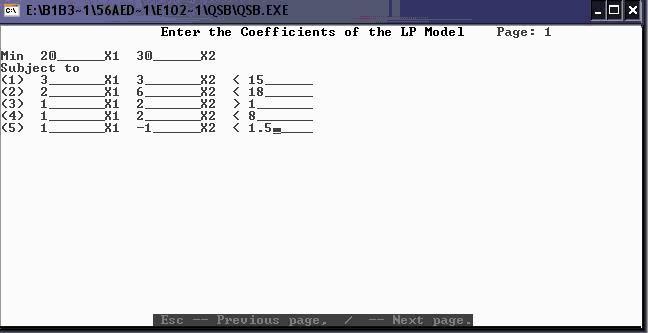
Ввод ограничения y3:

Полученные и сохранённые данные в файле:

NAME LAB3

ROWS

N OBJECTIV

L C1

L C2

G C3

L C4

L C5

COLUMNS

X1 OBJECTIV +20.0000

X1 C1 +3.00000

X1 C2 +2.00000

X1 C3 +1.00000

X1 C4 +1.00000

X1 C5 +1.00000

X2 OBJECTIV +30.0000

X2 C1 +3.00000

X2 C2 +6.00000

X2 C3 +2.00000

X2 C4 +2.00000

X2 C5 -1.00000

RHS

RHS C1 +15.0000

RHS C2 +18.0000

RHS C3 +1.00000

RHS C4 +8.00000

RHS C5 +1.50000

BOUNDS

LO BOUNDS X1 +.500000

UP BOUNDS X1 +4.00000

ENDATA

2) Решение симплекс-методом:

При решении симплекс-методом выводятся последовательно симплекс-таблицы: для каждой итерации симплекс-метода. В каждой таблице усиленной яркостью выделяются разрешающий элемент, а также имена меняющихся местами переменных: входящей (entering) в базис и выводимой (leaving) из базиса.

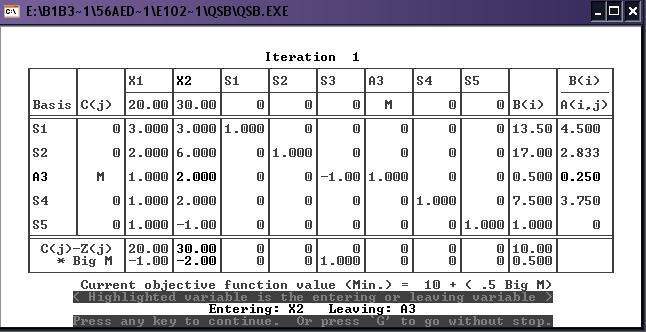
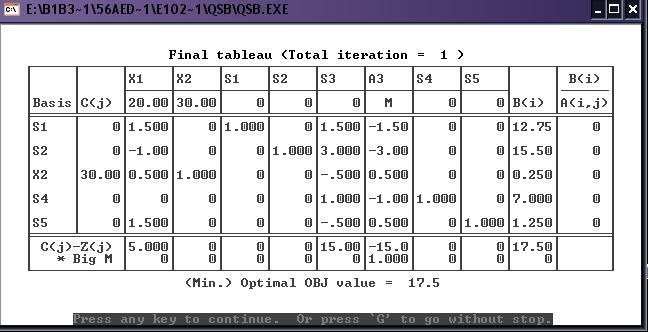
3) Полные результаты:

Выведем полные результаты решения так, чтобы кроме собственно значений переменных в точке оптимального решения получить также границы изменения параметров задачи, в пределах которых решение продолжает оставаться оптимальным (т.е. получить результаты исследования на чувствительность). При этом значение переменных в точке оптимального решения, границы (пределы чувствительности) для коэффициентов целевой функции и для правых частей ограничений выводятся в отдельных таблицах. Вывод пределов чувствительности соответствует параметрическому исследованию решения на чувствительность с помощью программ параметрического анализа (PAROBJ и PARRHS) ППП МикроЛП.

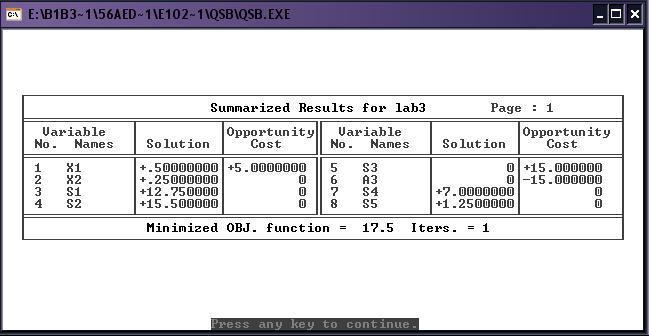
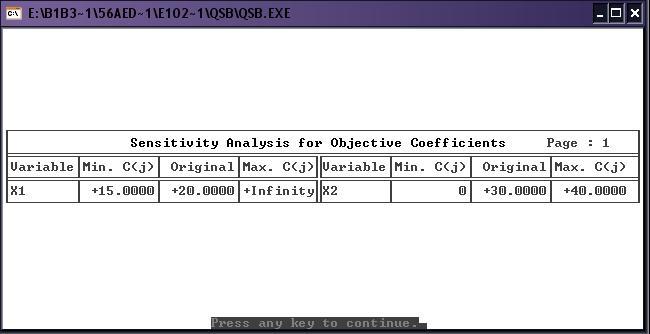
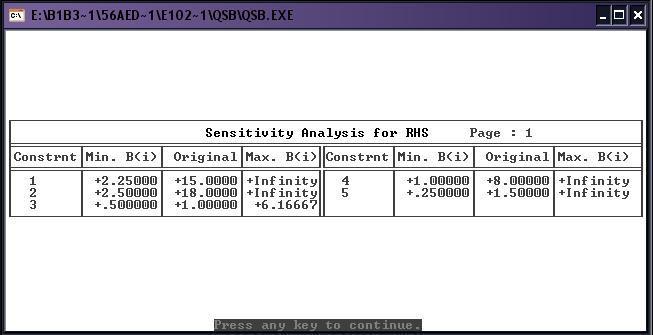
Задача на максимизацию:

1) Ввод новой задачи:

Диалоговая настройка модели:

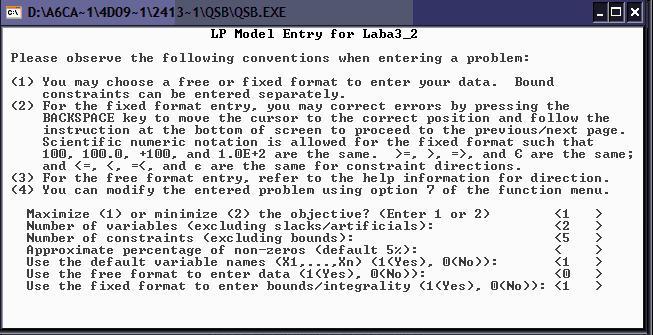
Ввод данных:

Ввод ограничения y3:

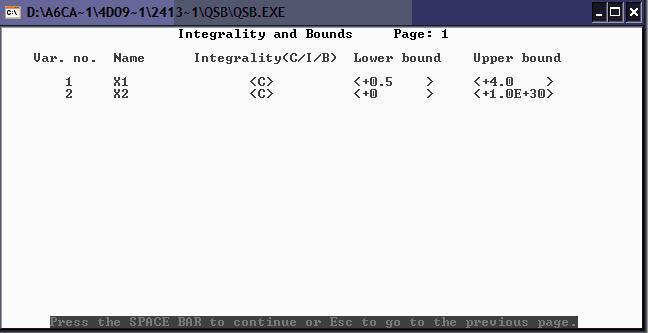
Полученные и сохранённые данные в файле:

NAME LAB3

ROWS

N OBJECTIV

L C1

L C2

G C3

L C4

L C5

COLUMNS

X1 OBJECTIV -20.0000

X1 C1 +3.00000

X1 C2 +2.00000

X1 C3 +1.00000

X1 C4 +1.00000

X1 C5 +1.00000

X2 OBJECTIV -30.0000

X2 C1 +3.00000

X2 C2 +6.00000

X2 C3 +2.00000

X2 C4 +2.00000

X2 C5 -1.00000

RHS

RHS C1 +15.0000

RHS C2 +18.0000

RHS C3 +1.00000

RHS C4 +8.00000

RHS C5 +1.50000

BOUNDS

LO BOUNDS X1 +.500000

UP BOUNDS X1 +4.00000

ENDATA

2) Решение симплекс-методом:

При решении симплекс-методом выводятся последовательно симплекс-таблицы: для каждой итерации симплекс-метода. В каждой таблице усиленной яркостью выделяются разрешающий элемент, а также имена меняющихся местами переменных: входящей (entering) в базис и выводимой (leaving) из базиса.

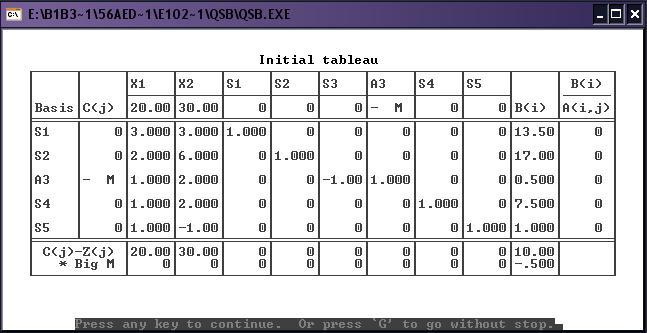
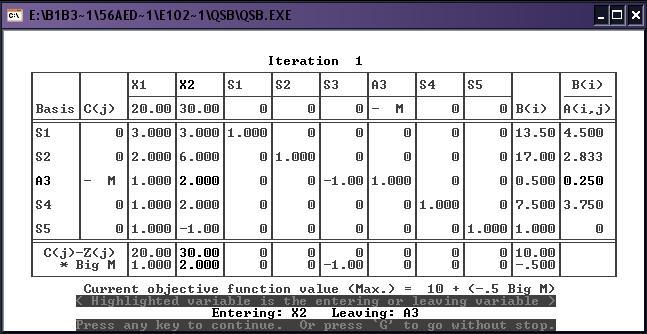
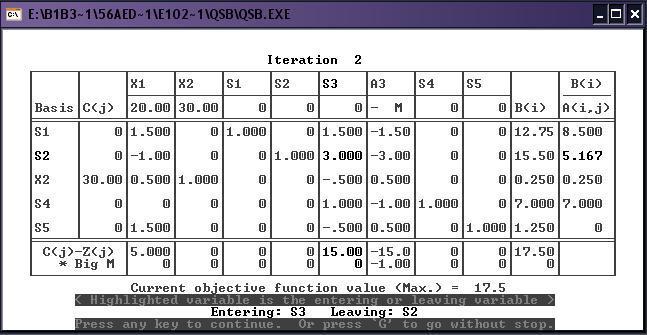
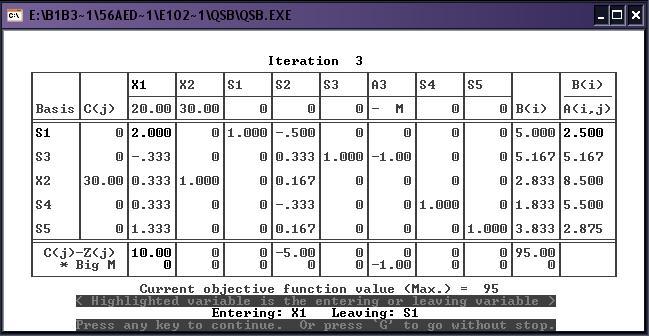
3) Полные результаты:

Выведем полные результаты решения так, чтобы кроме собственно значений переменных в точке оптимального решения получить также границы изменения параметров задачи, в пределах которых решение продолжает оставаться оптимальным (т.е. получить результаты исследования на чувствительность). При этом значение переменных в точке оптимального решения, границы (пределы чувствительности) для коэффициентов целевой функции и для правых частей ограничений выводятся в отдельных таблицах. Вывод пределов чувствительности соответствует параметрическому исследованию решения на чувствительность с помощью программ параметрического анализа (PAROBJ и PARRHS) ППП МикроЛП.

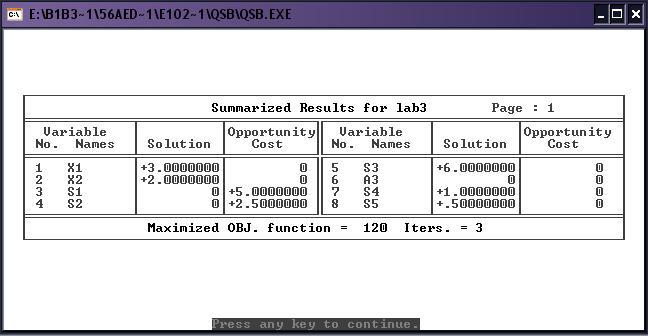
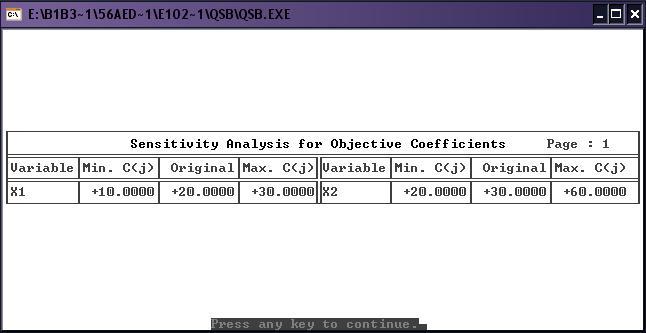
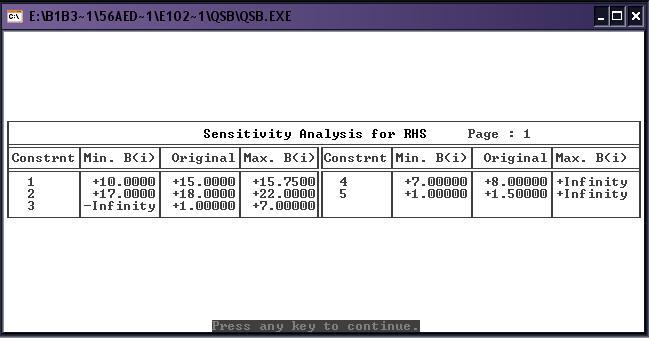
Выводы:

В данной лабораторной работе мы ознакомились с пакетом прикладных программ QSB+, при помощи которого решили задачу линейного программирования. Полученные результаты совпали с результатами в 1 лабораторной работе, т.е.

Точка max имеет координаты: X₁ = 3.00, X₂ = 2.00

Точка min имеет координаты: X₁ = 0.50, X₂ = 0.25

Кроме того, решили задачу геометрически. Этот способ решения хорош тем, что

графический ражим предоставляет возможности перемещения (поворота, сдвига) геометрического образа целевой функции и геометрических образов ограничения. Это позволяет наглядно представить себе задачу.

10