3.9. Эффект Джоуля – Томсона в газе Ван-дер-Ваальса

Из уравнения Ван-дер-Ваальса

найдем производную

Так как – функция одной переменной , то

. (3.9.1)

Подставив выражение (3.9.1) в (3.8.15), получим

. (3.9.2)

Если выражение, стоящее в числителе формулы (3.9.2) равно нулю

, (3.9.3)

то и т. е. газ Ван-дер-Ваальса в дроссель-эффекте не изменяет температуру.

Температуру, удовлетворяющую равенству (3.9.3), называют температурой инверсии и обозначают :

. (3.9.4)

На рис. 55 представлена зависимость температуры инверсии от молярного объема (кривая инверсии).

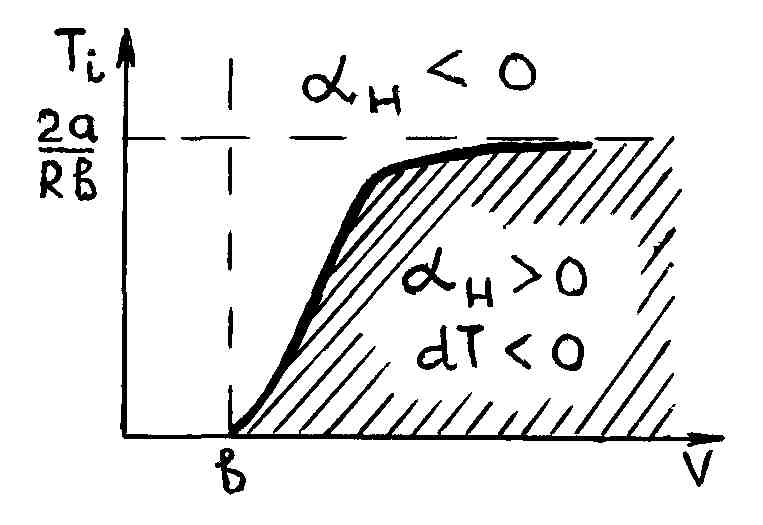
Р и с. 55

Любая точка на кривой инверсии с координатами ( ) определяет исходные (до проталкивания через дроссель) молярный объем и температуру рабочего вещества. Следовательно, после просачивания вещества с такими начальными параметрами через дроссель его температура не изменится и останется равной .

Если величина, стоящая в квадратной скобке формулы (3.9.2), больше нуля, что равносильно неравенству

, (3.9.5)

то и Это означает, если исходная температура рабочего вещества , то в дроссель-эффекте газ Ван-дер-Ваальса охлаждается, и, таким образом, всем точкам, расположенным ниже кривой инверсии отвечает положительный эффект Джоуля – Томсона (рис. 55).

Наоборот, всем точкам расположенным выше кривой инверсии, начальная температура газа которых , коэффициент Джоуля – Томсона и , т. е. газ Ван-дер-Ваальса при этом нагревается (отрицательный дроссель-эффект).

Если выполняется условие т. е. объем, занимаемый самими молекулами, значительно меньше объема газа, то, как следует из формулы (3.9.4),

(3.9.6)

Из сравнения выражений для критической температуры и температуры инверсии (3.9.6) следует, что

(3.9.7)

Из последнего соотношения видно, что температура инверсии для всех веществ значительно больше критической. Приведем экспериментальные значения температуры инверсии для некоторых веществ: для углекислого газа – 1500 К, для кислорода – 893 К, для азота – 621 К, для воздуха – 603 К, для водорода – 204 К, для гелия – 40 К.

Для всех газов, кроме водорода и гелия, температуры инверсии значительно выше комнатной температуры. Поэтому эти газы, взятые при исходной температуре, равной комнатной, будут всегда охлаждаться при дроссель-эффекте. У водорода и гелия температура инверсии намного меньше комнатной, поэтому они при дросселировании нагреваются. Следовательно, для получения положительного дроссель-эффекта ( ) необходимо предварительное глубокое охлаждение водорода и гелия.

В заключение заметим, что процесс Джоуля – Томсона является существенно необратимым. В самом деле, из выражения (3.8.11) при следует:

(3.9.8)

Так как при дроссель-эффекте всегда , то из последнего соотношения вытекает, что , что указывает на необратимость указанного процесса.

3.10. Сжижение газов. Получение низких и сверхнизких температур

Как нам известно, вещество будет находиться в жидком состоянии, если средняя кинетическая энергия его молекул порядка средней потенциальной энергии их взаимодействия. Для газов температура, при которой они сжижаются, достаточно низкая.

Различают два метода глубокого охлаждения газов: метод адиабатного расширения с совершением газом внешней работы и метод, основанный на использовании дроссель-эффекта.

Суть охлаждения газа в первом методе следует из первого закона термодинамики

в выражении которого при адиабатном расширении и т. е.

Последнее неравенство свидетельствует о том, что внутренняя энергия газа при адиабатном расширении уменьшается, что равносильно уменьшению его температуры.

Можно показать, что процесс обратимого адиабатного расширения (с отдачей внешней работы) обеспечивает более эффективное с точки зрения термодинамики охлаждение газа, чем процесс адиабатного дросселирования, т. е. необратимого адиабатного расширения. В настоящее время для сжижения газов используются такие аппараты, в которых метод адиабатического расширения с совершением внешней работы комбинируется с методом дросселирования.

Все известные газы, за исключением неона, водорода и гелия, достаточно легко сжижаются на этих машинах, т. е. их температура инверсии намного выше комнатных. Температуры инверсии неона, водорода и гелия значительно ниже комнатных, поэтому их предварительно охлаждают ( – жидким азотом, – жидким водородом).

Наиболее низкой температурой кипения при атмосферном давлении обладает жидкий гелий: К. Понизить температуру кипения можно откачкой паров гелия. Таким способом получена температура 0,69 К. Дальнейшее понижение температуры оказывается невозможным ввиду легкой испаряемости жидкого гелия, в результате которой насосы не успевают откачивать пары и понижать давление.

Поэтому для получения сверхнизких температур применяют так называемый метод адиабатного магнитного охлаждения. Сущность этого метода основана на том, что энтропия является мерой беспорядка в системе. Мы знаем, что с уменьшением температуры энтропия системы убывает, уменьшается при этом и беспорядок в ней. Однако беспорядок может быть связан и с другим параметром, характеризующим систему. В методе магнитного охлаждения таким параметром выступает степень беспорядка в расположении магнитных моментов молекул некоторых парамагнитных солей типа квасцов. Молекулы этих солей обладают заметным собственным магнитным моментом. При отсутствии магнитного поля суммарный магнитный момент соли вследствие хаотического теплового движения равен нулю. При увеличении интенсивности магнитного поля, налагаемого на соль, элементарные магниты становятся более параллельными направлению магнитного поля, вследствие этого степень магнитного беспорядка уменьшается. Уменьшается при этом и энтропия, связанная с ним.

На рис. 56 изображена зависимость энтропии парамагнитной соли от температуры при отсутствии магнитного поля и при его наличии .

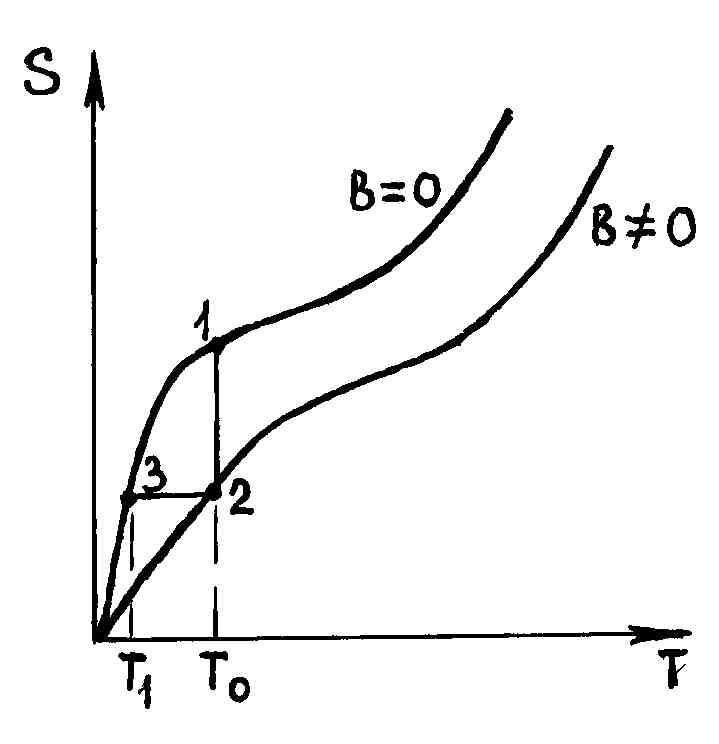
Р и с. 56

Из рис. 56 видно, что при любой температуре энтропия соли при наличии магнитного поля меньше энтропии соли при отсутствии этого поля. Это и понятно, ведь при наложении магнитного поля система имеет меньший беспорядок в ориентации элементарных магнитов, потому ее энтропия меньше.

Представим энтропию парамагнетика как сумму энтропии , связанную с хаотическим тепловым беспорядком, и энтропию , обусловленную беспорядком в расположении магнитных моментов молекул:

. (3.10.1)

Если с параметрами парамагнитной соли провести обратимые изменения в адиабатных условиях, то, как мы знаем, энтропия в этом процессе сохранится постоянной, т. е.

. (3.10.2)

Запишем последнее равенство для двух состояний. Затем вычтем одно из другого. В результате получим

. (3.10.3)

Опыт по охлаждению парамагнитной соли до сверхнизких температур проводится следующим образом. Ее вначале помещают в жидкий гелий и охлаждают до температуры 0,69 К описанным выше способом. Затем включают магнитное поле и при постоянной температуре К намагничивают. Процесс изотермического намагничивания изображен на рис. 56 прямой 12. При этом магнитная часть энтропии уменьшится на величину . Тогда, как следует из равенства (3.10.3), на такую же величину возрастет тепловая часть энтропии, что приведет к повышению температуры соли. Выделяющееся при этом тепло поглощается жидким гелием и, если масса гелия намного больше массы соли, это тепло не приведет к заметному повышению температуры гелия, т. е. процесс 12 останется изотермическим. После этого жидкий гелий сливают, т. е. изолируют соль от жидкого гелия, и медленно (обратимо) адиабатно размагничивают. Процесс размагничивания изображен на рис. 56 (отрезок 23), т. к. при адиабатном процессе . В этом случае магнитная часть энтропии возрастет на величину , а тепловая уменьшится на такую же величину. Это приведет к охлаждению соли до температуры К.

В настоящее время методом размагничивания ядерных магнитных моментов некоторых веществ получены температуры К, а методом, сочетающим лазерное охлаждение и ускоренное испарение, достигнуты температуры К.

184