Глава 3. Реальные газы

3.1. Экспериментальные изотермы. Критическая точка

Реальные газы отличаются от идеальных тем, что молекулы этих газов имеют конечные собственные объемы и связаны между собой сложными силами взаимодействия. При высоких давлениях и достаточно низких температурах реальные газы конденсируются, т. е. переходят в жидкое состояние, чего принципиально не может быть с идеальными газами.

В 1861 году ирландский физико-химик Т. Эндрюс экспериментально исследовал зависимость давления углекислого газа от объема при изотермическом сжатии. На рис. 47 схематично представлены результаты опытов, подобных опытам Т. Эндрюса. Рассмотрим изотерму АВСD.

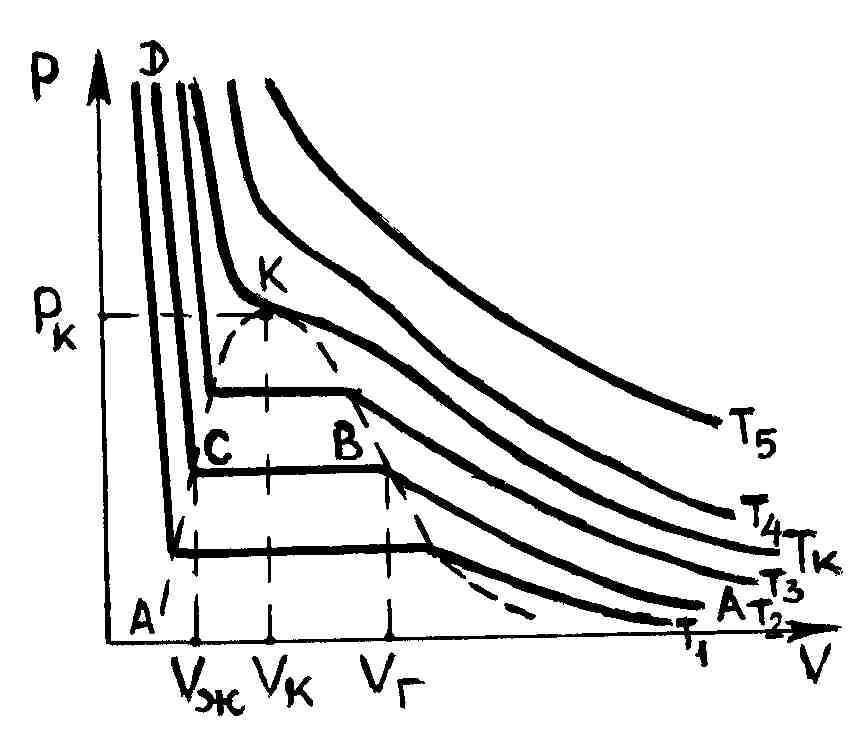
Р и с. 47

На участке АВ уменьшение объема, занятого газом, сопровождается увеличением давления сначала обратно пропорционально объему, затем все медленнее.

В точке В начинается конденсация газа и продолжается при постоянном давлении, называемом давлением насыщенных паров, до точки С. В точке С процесс конденсации газа заканчивается, при дальнейшем уме-ньшении объема осуществляется сжатие жидкости (участок СD), сопровождающееся быстрым ростом давления, свидетельствующее о том, что жидкость слабо сжимаема. При уменьшении давления, действующего на жидкость, вещество пройдет те же состояния в обратном порядке: оно расширится по пути DС до точки кипения, произойдет испарение (путь СВ), а затем получившийся пар расширится до исходного давления (точка А).

На участке ВС не только давление, но и температура постоянны. Крайним точкам отрезка ВС соответствуют однофазные состояния вещества: точке С (объем ) – жидкое, а точке В (объем ) – газообразное. В промежуточном двухфазном состоянии с объемом V часть вещества с количеством молей находится в жидком, а часть с количеством молей – в газообразном состоянии. Определим отношение количества молей жидкой и газообразной фаз в объеме .

Объем одного моля жидкой и газообразной фаз вещества соответственно равны:

. (3.1.1)

Объем V содержит молей жидкой фазы и молей газообразной фазы, поэтому этот объем можно представить в виде суммы объемов жидкой и газообразной фаз следующим образом:

. (3.1.2)

После простых преобразований из выражения (3.1.2) находим искомое отношение

. (3.1.3)

Умножая числитель и знаменатель левой части выражения (3.1.3) на молярную массу вещества, получим аналогичное отношение для масс жидкой и газообразной фаз:

. (3.1.4)

Таким образом, отношение масс жидкости и насыщенного пара в произвольном двухфазном состоянии определяемом объемом , равно отношению отрезков, на которое делит участок ВС точка, соответствующая объему (рис. 47). Из формулы (3.1.4) легко видеть, что, чем ближе значение молярного объема к , тем большая часть вещества находится в жидком состоянии и тем меньшая – в газообразном. И, наоборот, чем ближе объем к , тем большая часть вещества находится в газообразном состоянии, и тем меньшая его часть приходится на жидкость.

На рис. 47 представлены изотермы газа при различных температурах Из рисунка видно, что с ростом температуры горизонтальный участок, соответствующий двухфазному состоянию вещества, уменьшается и при некоторой температуре , называемой критической, стягивается в точку . Изотерма, соответствующая температуре , называется критической изотермой, точка которой является точкой перегиба.

Из рис. 47 также видно, что с ростом температуры растет молярный объем , занимаемый жидкостью, что равносильно уменьшению ее плотности . И, наоборот, с ростом температуры уменьшается молярный объем , занимаемый газом, что равнозначно увеличению его плотности . В критическом состоянии и т. е. в состоянии, определяемом критическими параметрами , исчезает всякое различие между жидкостью и ее насыщенным паром.

При температурах, больших критической, отсутствует область двухфазных состояний, вещество находится в газообразном состоянии. Это объясняется тем, что при температурах , кинетическая энергия поступательного движения молекул намного больше потенциальной энергии их взаимодействия и, естественно, вещество в таких условиях может находиться только в виде газа. Следовательно, даже сверхвысокими давлениями невозможно газ перевести в жидкое состояние, если его температура выше критической. Поэтому в XIX в. потерпели неудачу первые попытки сжижения некоторых газов, так как комнатная температура, при которой начиналось их сжатие, была значительно больше критической температуры. В качестве примера приведем экспериментальные значения критической температуры для некоторых веществ: для воды для углекислого газа , для кислорода , для азота для водорода , для гелия . Как видно из приведенных чисел, выбор Т. Эндрюсом углекислого газа для опытов был весьма удачен.

Если соединить между собой левые концы горизонтальных участков опытных изотерм, соответствующих двухфазному состоянию вещества, а затем то же самое проделать с правыми концами, то получится колокольного вида кривая АKВ, которая совместно с частью DK критической изотермы разделит плоскость на три области (рис. 48).

Р и с. 48

Пограничная кривая AK, называемая кривой кипения, отделяет однофазную область 1 жидкого состояния вещества от двухфазной области 2 насыщенного пара. Пограничная кривая конденсации BK отделяет двухфазную область 2 от однофазной области 3 газообразного состояния вещества. При давлениях, больших критического , отсутствует область двухфазного состояния. Вещество в этом случае может находиться или в газообразном или в жидком состоянии. Границей между ними служит часть DK критической изотермы.

Наличие критической изотермы четко показывает, что между жидким и газообразным состояниями вещества нет принципиального качественного различия. В самом деле, из газообразного состояния вещество можно перевести в жидкое состояние , по пути минуя область 2 двухфазного состояния (рис. 48). При этом нигде не будет происходить скачкообразное изменение состояния, вещество будет на всем пути перехода однородным.